Algorithm
Review
1. 高层架构
2. OK, Result?
Tips
Share

Algorithm

https://dreamume.medium.com/leetcode-834-sum-of-distances-in-tree-523031b6a689

Review

Improved Alerting with Atlas Streaming Eval

流警告评估扩展比传统选时间序列数据库要好很多
它允许我们克服时间序列数据库的高维度/cardinality 限制
它支持更多激进的使用案例

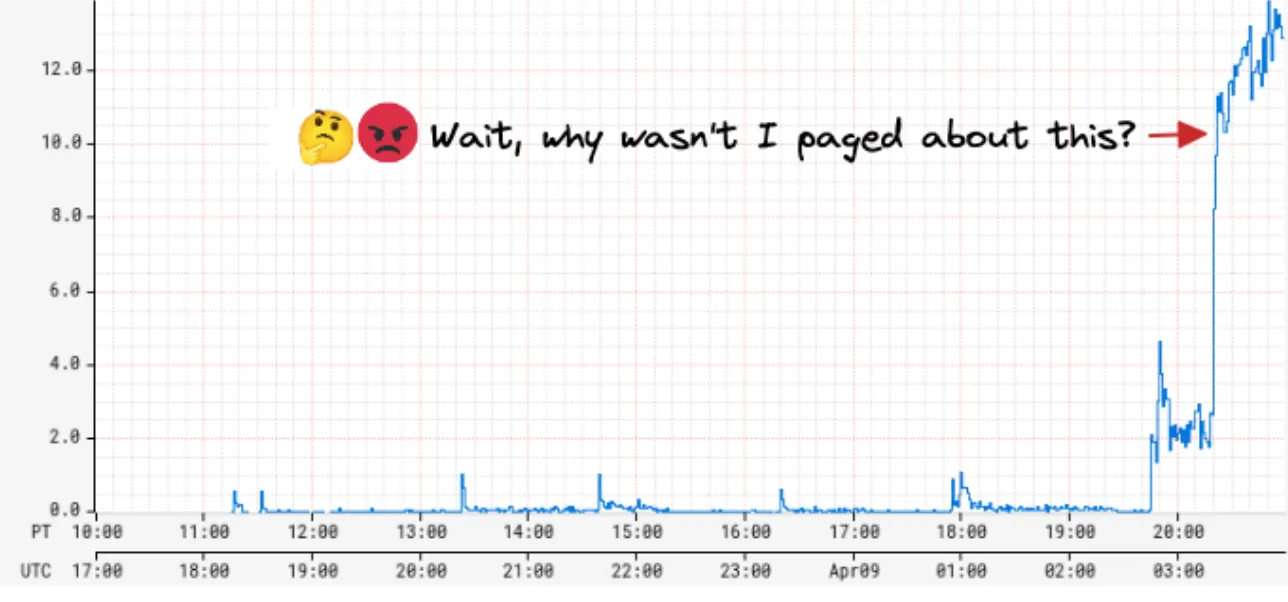
工程师想要他们的警告系统为实时，可靠且可动作化。当动作能力是主观的且可基于用户案例改变，可靠性是不可协商的。即错误的正面是不好的但错误的负面绝对是最坏的

几年前，我们被我们的 SRE 团队呼叫由于我们的度量警告系统的严重应用程序警告延迟 45 分钟才到达！当我们调研警告延迟，我们发现配置警告的数量最近戏剧性地增加了 5 倍！警告系统查询 Atlas，我们的时间系列数据库为每个配置的警告查询一个任务，且看到评估瓶颈速度和过度的回退尝试。这样，增加了一个警告两次连续检查的时间，导致对所有警告的全局下降。我们进一步的调查，我们发现一个用户编程式地创建了数万个新的警告。这个用户代表了一个 Netflix 平台团队，且他们的目标是构建他们用户的警告自动处理

然而我们可以立即灭火通过禁止新的警告创建，这个事件引起了对我们警告系统扩展性的担忧。我们也从 Netflix 其他平台团队听到他们想要构建相似的对他们用户的自动工具，对某一时刻我们的状态，对其他人不会影响中位时间检测（MTTD）。我们看到了接下来 6 个月警告查询大幅增加的趋势

因为查询 Atlas 是瓶颈，我们首先的直觉是扩展它来满足增加的警告查询需求；然而，我们很快意识到增加 Atlas 的成本是不可接受的。Atlas 是一个内存时间系列数据库每天输入几十亿的时间系列且保留最近两周的数据。它是 Netflix 在尺寸和成本上最大的服务。当 Atlas 基于计算和存储分离架构，且我们理论上可扩展查询层来满足增长的查询需求，每个查询，无论它的类型，有一个数据组件需要推到存储层。为服务降低查询的增长数量，内存存储层也需要扩展，且这明显会导致高贵的存储成本更高得多。更进一步，通常的数据库优化比如缓存最近查询数据对警告查询有作用，最近接收到的数据点需要正确性。例如，这个警告查询检查是否错误作为总 RPS 的百分比超过一个 50% 阙值对最近 5 分钟内的 4 分钟：

name, errors, :eq, :sum,
name, rps, :eq, :sum,
:div,
100, :mul,
50, :gt,
5, :rolling-count, 4, :gt,

如果最近时间段接收到的数据点导致对这个查询的一个正估计，其依赖脏/缓存数据增加了 MTTD 或一个错误的负的探测结果，至少直到丢失的数据被获取和评估。对我们来说明显的是我们需要以一个基本不同的方式解决扩展问题。因此，我们开始通过实时流度量来降低警告评估的路径

高层架构

在高层，避免整个过程需要查询 Atlas 数据库且交易警告查询到流评估

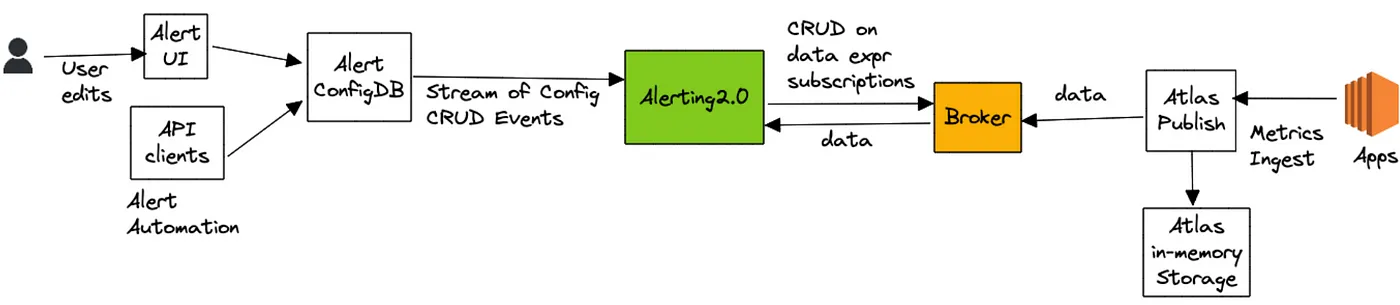
警告查询通过我们的警告界面或通过 API 客户端提交，然后保存到一个自定义配置数据库支持流配置更新（全快照 + 更新通知）。警告服务接收到这些配置更新且哈希通过均衡 Edda Slots 评估其中一个节点的每个新的或更新的警告查询。节点负责评估一个查询，通过分解为一系列数据表达和订阅到一个上游代理服务。数据表达定义什么数据需要被追源来评估一个查询。对上面列出的查询例子，数据表达为 name,errors,:eq,:sum 和 name,rps,:eq,:sum。代理服务作为一个订购管理者映射一个数据表达到一系列订购。另外，它也维护一个所有活跃数据表达的查询索引，其咨询识别是否一个输入数据点对一个活跃订阅者有兴趣

接着，警告服务（通过 atlas-eval 库）映射接收到一个数据表达的数据点到需要它们的警告查询。对警告查询解决多个数据表达，我们在发射累积值到最终评估步骤之前对齐同一时刻这些数据表达的输入数据点。对上述例子，最终评估步骤负责计算比例和维护 rolling 统计，其记录过阙值比例的间隔数，如下表所示：

表达	t1	t2	t3	t4	t5
name,errors,:eq,:sum,	1	3	5	4	7
name,rps,:eq,:sum,	6	7	9	6	9
rolling 统计（错误率）	16%	42%	55%	66%	77%

atlas-eval 库支持流评估大多数而不是全部 Atlas 支持的查询，数据，数学和状态操作。一些操作比如 offset，integral，des 在流路径上不支持

OK, Result?

最重要的，我们成功地基于架构减轻了我们初始的扩展问题。今天，我们运行了相比几年前 20 倍的查询数，只是用了扩展了 Atlas 存储层的一些成本来服务相同的卷。Netflix 的多个平台团队编程式地产生和维护警告而不用担心影响其他系统的用户。我们可维护中位时间检测（MTTD）的强 SLA 而不需要在意被系统评估的警告数

另外，流评估允许我们在高 cardinality 下释放限制，之前我们的用户由于 cardinality 限制运行的警告查询被 Atlas 后端拒绝现在则可以正确的在流路径上得到检查。另外，我们可使用 Atlas 流在非常高的 cardinality 用户案例下监控和警告，比如自由形式日志数据的度量

最后，我们切换 Telltale，我们的整体应用程序健康监控系统，从推一个度量缓存到使用实时 Atlas 流。基本的思想在 Telltale 上是检测 SLI 度量的异常（例如，延迟，错误率等等）。当这样的异常被检测，Telltale 可用上流或下流服务激发的相似的度量计算校正。另外，它也能计算 SLI 度量和自定义度量比如源于度量的日志之间的校正。这证明对缩减中位时间来恢复（MTTR）是有价值的。例如，我们可现在关联增长的错误率与发生在日志中特殊异常的增长率且指向一个典型的堆栈跟踪，如下图所示：

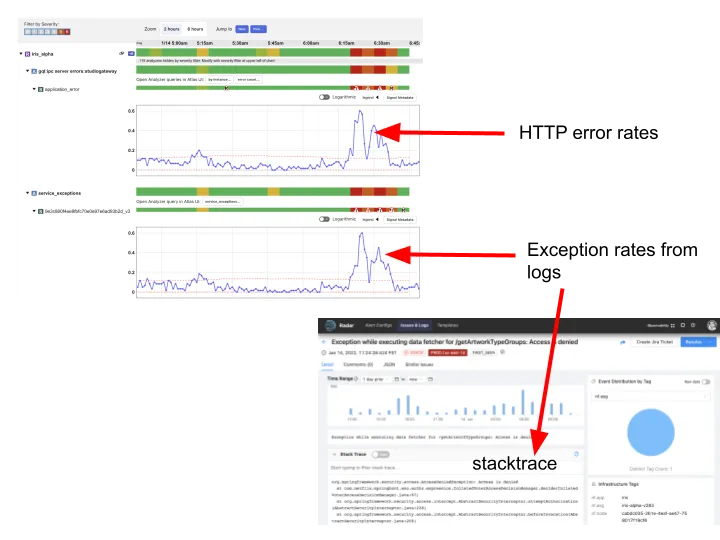
我们的日志流水线指纹每一条日志消息且附带一个（非常高 cardinality）指纹 tag 到一个日志事件统计器，其然后发射到 Atlas 流。Telltale 消费这个度量在流中确定指纹在 SLI 度量中看到的异常相关。一旦一个异常被发现，我们用指纹哈希查询日志后端来获得典型的堆栈追踪。更重要的是我们现在可确定相关异常发生在距离被影响的服务 N 跳的服务上。一个系统像 Telltale 变得更高效当更多的服务上线时，因为否则它找到问题源会变得更困难，特别在基于微服务的架构中。几年前，只有一百个服务使用 Telltale；多亏 Atlas 流我们现在管理 Netflix 上数千个其他服务

最后，我们意识到一旦你在监控查询数量上删除限制，且开始支持更高度量维度/cardinality 而不影响系统的成本/性能配置，它对许多令人激动的心可能性打开了天窗。例如，为使警告更可操作，我们可现在计算 SLI 异常跟自定义度量在高 cardinality 维度下的相关性，例如一个评估 HTTP 错误率的警告可指向一组特定用户，通过链接精确相关典型。这帮助开发者重现

过渡到流路径对我们来说是一个长期的过程。挑战之一是当流路径不符合查询 Atlas 数据库返回时调试场景很困难。特别是要么 Atlas 中数据无效或查询不支持因为 cardinality 限制时。这是让我们花费数年才达成的原因之一。早期的信号显示流范型在观测时可帮助追踪一个 cardinal 问题 - 度量和事件垂直之间高效相关（日志，和未来潜在的追踪），且我们激动于探索一般化对检测呈现的机会

Tips

Binary Lifting

经典问题

Binary Lifting 最常见的应用例子如下：

设 G 为有 N 个节点的有根树。对形如 (K, V) 的查询 Q 我们想要找到节点 V 在树中的第 K 个祖先

一个简单的解决方案是对每个节点构建一个到其直接父节点的边。然后，遍历 K 条边来获得查询结果。这个方式时间复杂度为 O(NQ)。我们尝试通过添加一些跳边来改进它

一个跳边是从一个节点到一个任意祖先的边。这些跳边允许我们在一次操作中遍历更大的边范围。让我们开始构建每个点的跳边到它的第 2 个祖先，第 4 个祖先，第 8 个祖先等等。注意上图只是这些跳边的一个子集，因为完整的绘制会显得图片太凌乱

让我们定义一个跳边的长度为遍历正常边的个数。例如，上图所有蓝色边有长度 4。我们可递归计算这些跳边

更形式化的，我们记 f(h, i) 为 i 的第 2^h 代祖先。可用如下递归公式：f(h, i) = f(h - 1, f(h - 1, i))。我们可分割 K 为 2 的指数，例如，设要寻找 9 的第 7 代祖先。因为 7 = 4 + 2 + 1，我们可遍历蓝边从 9 到 5，红边从 5 到 3 和黑边从 3 到 2

这种方式时间复杂度为 O((N + Q)lgN)，空间复杂度为 O(Nlg2N)

可以做得更好吗？

在这个特殊例子中，我们可采用脱机方式查询（我们读取所有查询并一并解决它们）。我们将使用深度优先搜索且我们维护一个当前节点所有祖先的数组（包括它本身）。为维护这个祖先数组我们可简单操作如下：当从一个节点到它的儿子节点我们把儿子节点放入祖先数组的末尾且当从一个节点到它的父节点时从祖先数组末尾移除它。这样，当我们到达一个节点我们可以从访问祖先数组中获得答案。代码实现如下：

const int nmax = 200000;
vector<int> g[5 + nmax];
vector<pair<int, int>> queries[5 + nmax];

int solution[5 + nmax];
vector<int> ancestors;

void dfs(int node) {
  ancestors.push_back(node);

  for (int i = 0; i < g[node].size(); ++i)
    dfs(g[node][i]);

  for (int i = 0; i < queries[node].size(); ++i) {
    auto& [acc, id] = queries[node][i];
    if (acc < ancestors.size())
      solution[id] = ancestors[ancestors.size() - acc - 1];
    else
      solution[id] = -1;
  }
  ancestors.pop_back();
}

int main() {
  int n, q;
  cin >> n >> q;
  for (int i = 2; i <= n; ++i) {
    int x;
    cin >> x;
    g[x].push_back(i);
  }
  for (int i = 1; i <= q; ++i) {
    int x, k;
    cin >> x >> k;
    queries[x].push_back({k, i});
  }
  dfs(1);

  for (int i = 1; i <= q; ++i)
    cout << solution[i] << endl;

  return 0;
}

然而，如果我们得先回答一个查询然后才能是下一个查询时怎么办？不幸地是，这种情况下我们不能改进时间复杂度 O((N + Q)lgN)，然而我们可缩减内存的使用

一个方法是用时间换空间且改变跳边的长度的基。我们可重计算跳边长度为 D 的指数，D > 2

不牺牲执行时间？

我们可缩减内存到 O(N) 而不影响执行时间。我们可计算每个节点它的父节点且一个单跳边到任意祖先。当搜索第 K 个祖先我们尝试遍历跳边如果它没有超过第 K 个祖先。选择这些跳边的目标的一个方法是观察如下图：

记 x 的父为 $ parent_ {x} $。我们将添加跳边 $ x \to y $ 只在 $ parent_ {x} \to z $ 和 $ z \to y $ 存在且对任意 z 有相同的长度。容易看到我们可通过从顶向下在树中以 O(N) 的时间复杂度计算所有这样的跳边

通过使用这些边我们可在对数时间复杂度下到达第 K 个祖先，但这是不容易看出的。这个的证明非常长且使用 skew-binary 数系统。在论文 An appicative random access stack 中边界为 $ 3 \lfloor \lg{(N+1)} \rfloor - 2 $

源代码实现如下：

const int nmax = 200000;
int parent[1 + nmax];
int far[1 + nmax];
int level[1 + nmax];

int main() {
  int n, q;
  cin >> n >> q;
  for (int i = 2; i <= n; ++i)
    cin >> parent[i];

  level[1] = 1;
  for (int i = 2; i <= n; ++i) {
    level[i] = level[parent[i]] + 1;
    int father = parent[i];
    int father2 = far[father];
    if (far[father2] != 0 && 
        level[father] - level[father2] == level[father2] - level[far[father2]])
      far[i] = far[father2];
    else
      far[i] = father;
  }

  for (int i = 1; i <= q; ++i) {
    int node, k;
    cin >> node >> k;
    while (k > 0 && node > 0) {
      if (level[node] - k <= level[far[node]]) {
        k -= level[node] - level[far[node]];
        node = far[node];
      } else {
        --k;
        node = parent[node];
      }
    }
    if (node == 0) cout << -1 << endl;
    else cout << node << endl;
  }

  return 0;
}

另一种方法是选择 $ \frac{N}{\log{N}} $ 个任意节点且创建一个虚拟树其 x 和 y 的边表示 x 是 y 的祖先且它们之间没有其他选中的节点在路径上。我们可在虚拟树上使用 $ O(\frac{N}{\log{N}} * \log{N}) = O(N) $ 的内存计算跳边。为回答一个查询我们发现我们最接近的祖先是这个虚拟树的一部分且在虚拟树上找（这个祖先期望为距离在 $ \log{N} $ 的边因为我们随机选择的虚拟树节点）。我们可使用虚拟树跳边来尽可能接近第 K 个祖先。在没有跳边可使用后，我们可使用原始树的边，因为我们的目标期望在大约 $ \log{N} $ 距离的边

感谢 FairyWinx 提议的这个想法且我非常高兴看到一个确定性方法来达到 O(N) 的内存。下面是代码实现：

const int nmax = 200000;
const int lgmax = 20;
vector<int> g[5 + nmax];

// These are for the real tree
int parent[5 + nmax];
int level[5 + nmax];
int id[5 + nmax];

// There are for the virtual tree
int revid[5 + nmax / lgmax];
int level2[5 + nmax / lgmax];
int far[1 + lgmax][5 + nmax / lgmax];

void dfs(int node, int curParent) {
  if (id[node] > 0) {
    far[0][id[node]] = curParent;
    curParent = id[node];
  }

  for (int i = 0; i < g[node].size(); ++i) {
    int to = g[node][i];
    level[to] = level[node] + 1;
    dfs(to, curParent);
  }
}

int main() {
  mt19937 rng(steady_clock::now().time_since_epoch().count());
  int n, q;
  cin >> n >> q;
  for (int i = 2; i <= n; ++i) {
    cin >> parent[i];
    g[parent[i]].push_back(i);
  }

  for (itn i = 1; i <= n / lgmax; ++i) id[i] = i;
  shuffle(id + 1, id + n + 1, rng);

  level[1] = 1;
  dfs(1, 0);

  for (int i = 1; i <= n; ++i) {
    if (id[i] > 0) {
      revid[id[i]] = i;
      level2[id[i]] = level[i];
    }
  }

  for (int h = 1; h <= lgmax; ++h) {
    for (int i = 1; i <= n / lgmax;++i)
      far[h][i] = far[h - 1][far[h - 1][i]];
  }

  for (int i = 1; i <= q; ++i) {
    int node, k;
    cin >> node >> k;
    if (level[node] <= k) {
      cout << -1 << endl;
    } else {
      while (k > 0 && id[node] == 0) {
        node = parent[node];
        --k;
      }

      if (k > 0) {
        node = id[node];
        for (int i = lgmax; i >= 0; --i) {
          if (level2[node] - level2[far[i][node]] <= k) {
            k -= level2[node] - level2[far[i][node]];
            node = far[i][node];
          }
          node = revid[node];
        }
      }
      while (k > 0) {
        node = parent[node];
        --k;
      }
      cout << node << endl;
    }
  }

  return 0;
}

使用 Binary Lifting 计算最小公共祖先

另一个常见的 Binary Lifting 应用是计算两个节点的最小公共祖先（LCA）。在计算我们的跳边之前我们也应该计算每个节点的深度。为简化，让我们假设使用源方法创建跳边（使用 2 的指数）。设 x 和 y 为两个节点，为找到它们的 LCA 我们可应用如下策略：

假设 $ depth_ {y} \le depth_ {x} $，否则我们可让它们交换
设 $ K = depth_ {x} - depth_ {y} $ 且 z 为 x 的第 K 个祖先。x 和 y 的 LCA 即是 y 和 z 的 LCA。我们可用 z 替换 x 并假设 $ depth_ {x} = depth_ {y} $
如果 x == y 则 LCA 是 x。如果 x 的直接祖先跟 y 的直接祖先相同，则该直接祖先就是 LCA。否则，设 K 为小于或等于 $ depth_ {x} $ 的最高位 2 的次方。如果 x 的第 K 个祖先和 y 的第 K 个祖先不同，则我们可缩减问题为在 x 的第 K 个祖先和 y 的第 K 个祖先内找到 LCA，否则我们考虑更小的跳边

O(N) 内存方案对 LCA 查询也兼容。第 1 和 2 步是确定的，对第 3 步因为 $ depth_ {x} = depth_ {y} $，它们的跳边有相同的长度 K，这样我们可检查是否它们为相同节点。如果不是，则我们可缩减问题到第 K 个祖先之内，否则我们可缩减问题找他们的父节点的 LCA

O(NlgN) 内存的代码实现如下：

const int nmax = 200000;
const int lgmax = 20;

int level[1 + nmax];
int far[1 + lgmax][1 + nmax];

void getLca(int x, int y) {
  if (level[x] < level[y]) swap(x, y);

  for (int i = lgmax; i >= 0; --i) {
    if (level[y] + (1 << i) <= level[x])
      x = far[i][x];
  }
  if (x == y) return x;

  for (int i = lgmax; i >= 0; --i) {
    if (far[i][x] != far[i][y]) {
      x = far[i][x];
      y = far[i][y];
    }
  }

  return far[0][x];
}

int main() {
  int n, q;
  cin >> n >> q;
  for (int i = 2; i <= n; ++i)
    cin >> far[0][i];

  for (int h = 1; h <= lgmax; ++h) {
    for (int i = 1; i <= n; ++i)
      far[h][i] = far[h - 1][far[h - 1][i]];
  }

  for (int i = 2; i <= n; ++i)
    level[i] = level[far[0][i]] + 1;

  for (int i = 1; i <= q; ++i) {
    int x, y;
    cin >> x >> y;
    cout << getLca(x, y) << endl;
  }

  return 0;
}

O(N) 内存的代码实现如下：

const int nmax = 200000;
int parent[1 + nmax];
int far[1 + nmax];
int level[1 + nmax];

int getLca(int x, int y) {
  if (level[x] < level[y]) swap(x, y);

  while (level[y] < level[x]) {
    if (level[y] <= level[far[x]]) x = far[x];
    else x = parent[x];
  }
  if (x == y) return x;

  while (parent[x] != parent[y]) {
    if (far[x] != far[y]) {
      x = far[x];
      y = far[y];
    } else {
      x = parent[x];
      y = parent[y];
    }
  }

  return parent[x];
}

int main() {
  int n, q;
  cin >> n >> q;
  for (int i = 2; i <= n; ++i)
    cin >> parent[i];

  level[1] = 1;
  for (int i = 2; i <= n; ++i) {
    level[i] = level[parent[i]] + 1;
    int father = parent[i];
    int father2 = far[father];
    if (far[father2] != 0 && 
        level[father] - level[father2] == level[father2] - level[far[father2]])
      far[i] = far[father2];
    else
      far[i] = father;
  }

  for (int i = 1; i <= q; ++i) {
    int x, y;
    cin >> x >> y;
    cout << getLca(x, y) << endl;
  }

  return 0;
}

使用 Binary Lifting 来路径聚集

另一个使用 Binary Lifting 的有用应用是提取树上路径的信息。例如，如下问题：

设 T 为边带权重的树。对 Q 查询 (x, y) 我们想要从 x 到 y 的路径上的最大边权重

为解决这个问题我们可维护额外的跳边信息比如这个跳边上所有正常边的最大权重值。为提取 (x, y) 上最大的权重，我们首先定义 z 为 x 和 y 的最小公共祖先且分割路径 $ x \to y $ 为 $ x \to z $ 和 $ z \to y $。为找到路径 $ x \to z $ 的最大权重我们可简单分割它为跳边，且计算所有这些跳边的最大权重

不幸地是，Binary Lifting 在边的权重更新或树的结构被影响时不能扩展。对前者它需要使用 heavy light decomposition，后者需要使用 link cut tree。这些算法非常长且其实现单调乏味，所以尽量使用 Binary Lifting

因为我不能找到这样直接的问题，Minimum spanning tree for each adge 可视为这样的问题，其实现代码如下：

const int nmax = 200000;
const int lgmax = 20;
const int inf = 1000000000;

class Dsu {
public:
  Dsu(int n) {
    mult.resize(1 + n);
    for (int i = 1; i <= n; ++i) mult[i] = i;
  }

  int jump(int gala) {
    if (gala != mult[gala])
      mult[gala] = jump(mult[gala]);

    return mult[gala];
  }

  void unite(int gala, int galb) {
    gala = jump(gala);
    galb = jump(galb);
    if (gala == galb) return;

    mult[gala] = galb;
  }

  bool connected(int x, int y) {
    return jump(x) == jump(y);
  }
private:
  vector<int> mult;
};

struct Edge {
  int x;
  int y;
  int cost;
  int id;
  bool operator<(const Edge& other) { return cost < other.cost; }
};

long long solution[5 + nmax];
vector<pair<int, int>> g[5 + nmax];

int far[1 + lgmax][1 + nmax];
int farp[1 + lgmax][1 + nmax];
int level[5 + nmax];

int getLca(int x, int y) {
  if (level[x] < level[y]) swap(x, y);

  for (int i = lgmax; i >= 0; --i) {
    if (level[y] + (1 << i) <= level[x])
      x = far[i][x];
  }
  if (x == y) return x;

  for (int i = lgmax; i >= 0; --i) {
    if (far[i][x] != far[i][y]) {
      x = far[i][x];
      y = far[i][y];
    }
  }

  return far[0][x];
}

void dfs(int node, int parent) {
  for (int i = 0; i < g[node].size(); ++i) {
    int to = g[node][i].first;
    int cost = g[node][i].second;
    if (to != parent) {
      far[0][to] = node;
      farp[0][to] = cost;
      level[to] = level[node] + 1;
      dfs(to, node);
    }
  }
}

int main() {
  int n, m;
  cin >> n >> m;
  vector<Edge> edges;
  for (int i = 1; i <= m; ++i) {
    int x, y, cost;
    cin >> x >> y >> cost;
    edges.push_back({x, y, cost, i});
  }
  sort(edges.begin(), edges.end());
  vector<Edge> treeEdges, queryEdges;

  long long base{0};

  for (int i = 0; i < edges.size(); ++i) {
    int x = edges[i].x;
    int y = edges[i].y;
    if (dsu.connected(x, y) == 0) {
      base += edges[i].cost;
      dsu.unite(x, y);
      treeEdges.push_back(edges[i]);
    } else {
      queryEdges.push_back(edges[i]);
    }
  }

  // Here starts the relevant code
  for (int i = 0; i < treeEdges.size(); ++i) {
    int x = treeEdges[i].x;
    int y = treeEdges[i].y;
    int cost = treeEdges[i].cost;
    g[x].push_back({y, cost});
    g[y].push_back({x, cost});
  }

  dfs(1, 0);

  for (int h = 1; h <= lgmax; ++h) {
    for (int i = 1; i <= n; ++i) {
      far[h][i] = far[h - 1][far[h - 1][i]];
      farp[h][i] = max(farp[h - 1][i], farp[h - 1][far[h - 1][i]]);
    }
  }

  for (int i = 0; i < queryEdges.size(); ++i) {
    int x = queryEdges[i].x;
    int y = queryEdges[i].y;
    int lca = getLca(x, y);
    int res{0};
    for (int i = lgmax; i >= 0; --i) {
      if (level[lca] + (1 << i) <= level[x]) {
        res = max(res, farp[i][x]);
        x = far[i][x];
      }
    }
    for (int i = lgmax; i >= 0; --i) {
      if (level[lca] + (1 << i) <= level[y]) {
        res = max(res, farp[i][y]);
        y = far[i][y];
      }
    }
  }

  for (int i = 1; i <= m; ++i)
    cout << base + solution[i] << endl;

  return 0;
}

记笔记的重要性

最近又发生了一些事，因为忘了而导致懊悔、沮丧。因此有了要记笔记的想法。因为有些事情事到临头再去想，必然是会有些来不及的。即使你之前已做了很好的规划，但当前要记起时，也免不了遗漏

与其临时让大脑去艰难地回忆，不如记在笔记里，需要时拿出来看一下即可。这不是明显容易很多了吗？

需要一款记笔记的软件，功能不需要太复杂，需要能添加修改查看笔记，到期提醒功能。使用要简单方便。看看有什么软件先试用试用

目标是合理安排时间，让事情有条理，不要再丢三落四了

Weekly 080

Table of Contents

Algorithm

Review

高层架构

OK, Result?

Tips

经典问题

可以做得更好吗？

不牺牲执行时间？

使用 Binary Lifting 计算最小公共祖先

使用 Binary Lifting 来路径聚集

Table of Contents

Algorithm

Review

高层架构

OK, Result?

Tips

经典问题

可以做得更好吗？

不牺牲执行时间？

使用 Binary Lifting 计算最小公共祖先

使用 Binary Lifting 来路径聚集

Share