Table of Contents
Algorithm
Leetcode 2565: Minimum Reverse Operations
https://dreamume.medium.com/leetcode-2612-minimum-reverse-operations-69e9ec1c4ae2
Review
Making your code faster by taming branches
https://www.infoq.com/articles/making-code-faster-taming-branches/
关键要点
- 为更好的性能,现代处理器预测分支且执行猜测的指令。这是强有力的优化
- 程序员可能被错误低估分支预测错误对评测代码的代价,当人造的数据太短或太多预测时。分支错误预测的效果会很大。幸运地是,通常能够完全避免分支
- 重写你的代码使用更少的分支会使代码有更一致性的速度
- 需要适合的错误分支预测处理来优化性能
多数软件代码包含条件分支。在代码中,它们出现在 if else,循环和 switch 中。当统计一个条件分支,处理器检查一个条件且跳转到一个新的代码路径,如果分支被采用,或者继续执行接下来的指令。不幸地是,处理器可能只在执行玩之前的所有指令后知道是否一个跳转是必须的。为更好的性能,现代处理器预测分支且执行猜测的指令。这是一个强有力的优化。
然而猜测执行有一些限制。例如,在错误预测后处理器必须丢弃已作的工作且当分支预测失败时重新开始一次。幸运地是,处理器尽可能擅长识别范型且避免错误预测。尽管如此,一些分支本能地很难预测且它们会导致一个性能瓶颈
分支预测不容易被愚弄
程序员可能被错误低估分支预测错误对评测代码的代价,当人造的数据太短或太多预测时。现代处理器能学习预测数千个分支,这样一个短的测试可能不能暴露分支预测的代价,即使数据看上去是随机的
让我们考虑一个例子。假设我们想要解码十六进制数字。我们想要获得对应的整数值。一个合理的 C 函数如下
int decode_hex(char c) {
if (c >= '0' && c <= '9') return c - '0';
if (c >= 'A' && c <= 'F') return c - 'A' + 10;
if (c >= 'a' && c <= 'f') return c - 'a' + 10;
return -1;
}
一个程序员可随机产生一个字符串评测这样的函数。例如,在 C 中,我们可重复调用 rand 函数且选择 22 个十六进制数字的一个
char hex_table[] = {'0', '1', '2', '3', '4',
'5', '6', '7', '8', '9',
'a', 'b', 'c', 'd', 'e', 'f',
'A', 'B', 'C', 'D', 'E', 'F' };
void build_random_string(size_t length, char *answer) {
for (size_t i = 0; i < length; ++i)
answer[i] = hex_table[rand() % sizeof(hex_table)];
return answer;
}
然后可记录解码这些数字的时间。对好的测量,一个程序员可能运行这个测试几次且计算平均值。在多次测试之后,让我们描出对不同的字符串长度(1000,2000,…)每十六进制数字的错误预测分支数量。重要的是,我们重使用所有实验中的相同的输入字符串
使用一个标准服务器处理器(AMD Rome),我们发现对一个包含 3000 数字的字符串,在不到 20 次实验后每数值的错误预测分支数降到 0.015(1.5%)。对更短的字符串(1000 数字),错误分支预测数降得更快,在 8 次实验后降到 0.005。即一个标准服务器处理器在少于 10 次解码后可学习预测 1KB 十六进制随机字符串产生的所有分支
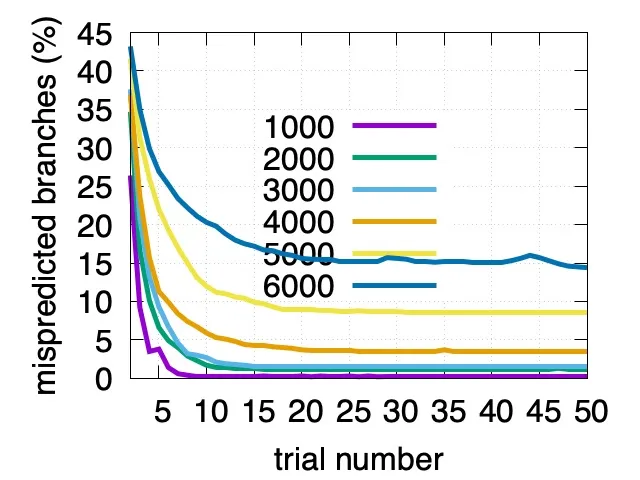
支持 just-in-time 编译器(比如 Java 或 Javascript)的编程语言中,它重复评测直到编译器优化了代码:如果测试太短,即使输入是随机的,我们也存在低估分支预测错误的代价
类似的,用人造数据运行测试,即使当数据集特别大,可能使得处理器高精度预测分支。假设我们使用从 0 到 65536 的数字替代随机字符串:0x00, 0x01, …
分支预测必须在数字和字符出现时预测。结果字符串(0000100021003100421052106310731084219421a521b521c631d631e731f7310842 … 8ce18ce29ce39ce4ade5ade6bde7bde8cef9cef …)不是随机的,但它使得预测数字和字符范型有效。使用相同的 AMD Rome 处理器,我们发现在这样一个长度为 131072 的字符串上错误预测分支的数量在第一次实验时接近为 0:每字节 0.002 次分支预测错误
分支预测错误可能代价很高
错误分支预测的影响可能会很大。让我们使用我们收集的不同长度随机十六进制字符串,且标出每输入数字 CPU 周期数及错误分支预测数。我们发现 CPU 周期数在每十六进制数字 5 周期到 20 周期变化,取决于错误预测分支数
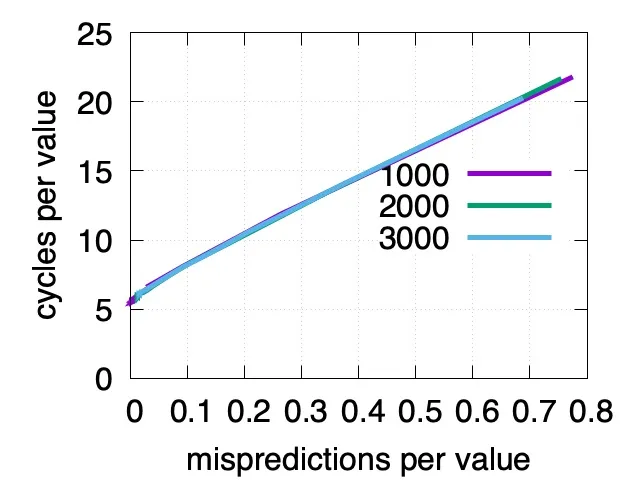
我们还不应该得出大量的分支预测错误是一个必要的考量因为可能有更重要的考量。例如,考虑一个大数组中的二进制搜索。限制是主存中内存访问延迟比分支错误预测成本更高
避免分支
性能分析工具,如 perf(Linux),xperf(Windows) 和 Instruments (macOS),可测量分支预测错误数。如果你手里有相关的问题,是否分支是一个问题呢?
幸运地是,通常可以完全避免分支。例如,为解码十六进制数字,我们可使用一个数组查找
int digittoval[256] = {
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, 0, 1,
2, 3, 4, 5, 6, 7, 8, 9, -1, -1,
-1, -1, -1, -1, -1, 10, 11, 12, 13, 14,
15, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, 10, 11, 12,
13, 14, 15, -1,...};
int hex(unsigned char c) {
return digittoval[c];
}
这个函数可编译为一个指令,没有分支。它可通过检查负整数来验证不合适的输入
这样,我们通常使用内存来替代分支:我们预计算分支并存储到一个简单数据结构中,比如数组
另一个避免分支的策略是做一些推测工作并抛出它们。例如,假设我们想要从整数输入数组中擦除所有负整数,在 C 中,我们可用一个循环和一个分支
for(size_t i = 0; i < length; i++) {
if(values[i] >= 0) {
values[pos++] = values[i];
}
}
我们假设这个函数叫 branchy,该代码检查输入并选择性地拷贝到新位置。如果我们很难预测哪个整数是负数,那这个代码是不高效的
幸运地是,多数编译器可以使用如下代码避免分支
size_t sign(int v) {
return (v >= 0 ? 1 : 0);
}
for(size_t i = 0; i < length; i++) {
values[pos] = values[i];
pos += sign(values[i]);
}
这个函数我们暂时称为 branchless。branchless 和 branchy 函数还是有点差异,编译器不能相互转换
即使不能移除所有分支,减少分支数用 “almost always taken” 和 “almost never taken” 可帮助编译器更好地预测剩下的分支。例如,如果我们使用循环一个个地解码,则在循环中我们对每个数字有一个预测分支
for (i = 0; i < length; ++i)
int code = decode_hex(input[i]);
// ...
对长的输入字符串,我们可减少减少一半的预测分支通过每次循环迭代处理两个输入字符
for (; i + 1 < length; i += 2) {
int code1 = decode_hex(input[i]);
int code2 = decode_hex(input[i + 1]);
// ...
}
在一个 AMD Rome 处理器上对 5000 数字的输入字符串,我们发现多次实验之后对简单循环的分支预测错误数是每数字 0.230,而对一次迭代处理两个数字的版本只有 0.165,减少了 30%
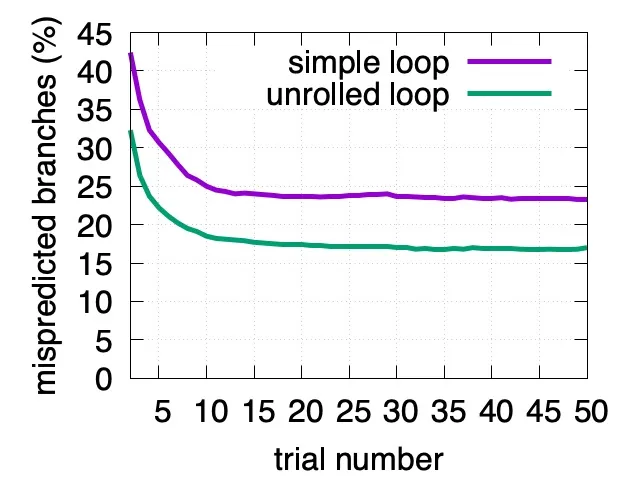
对这个现象的一个可能的简单解释是处理器使用历史上最新的分支预测将来的分支。无信息分支会让处理器减少做出好的预测的能力
当不能避免难的预测分支,我们可通常减少它们的数量。例如,当比较两个日期,把它们格式化为 YYYYMMDD 会比较方便,且比较结果的 8 字节字符串作为 64 为整数比较,可只使用一个指令
结论
对包含困难预测分支的代码进行评测是困难的,且程序员有时低估分支的代价。用更少的分支重写代码会让代码有更一致性的速度。预测错误分支的合适处理需要优化性能
Tips
Finding a needle in Haystack: Facebook’s photo storage
本文描述 Haystack,一个为 Facebook 图像应用程序优化的对象存储系统。Facebook 当前存储了超过 2600 亿个图片,大约 20PB。用户每周上传 10 亿个新图片(约 60 TB)且峰值时 Facebook 每秒处理超百万个图片。Haystack 提供了一个比之前的方式成本低且更高性能的解决方案,其对基于 NFS 的存储应用和网络有杠杆效果。我们重点关注到传统设计因 metadata 的查询导致过多的磁盘操作。我们小心地减少每图片 metadata 的操作让 Haystack 存储设备可在内存中处理所有 metadata 查询。这个处理节省磁盘操作来读取实际的数据并增加总体吞吐量
简介
共享图片是 Facebook 最流行的特性之一。到目前,用户已上传超过 650 亿张图片,Facebook 成为了全球最大的图片分享网站。对每个上传的图片,Facebook 会生成并存储四个不同大小的图片,转换了超过 2600 亿张图片和超过 20PB 数据。用户每周上传 10 亿张新图片(约 60 TB)且 Facebook 在峰值时每秒提供超过百万张图片。我们期望该数字会继续增长,则图片存储对 Facebook 的架构是一个显著的挑战
本文呈现 Haystack 的设计和实现。Facebook 的图片存储系统已在生产环境运营了 24 个月。Haystack 是一个对象存储,我们设计作为 Facebook 共享图片,其数据写一次,多次读,从不修改且很少删除。我们开发我们自己的图片存储系统因为传统的文件系统在我们的工作负载下性能低下
在我们的经验中,我们发现传统的 POSIX 文件系统的缺点是目录和每文件 metadata。对这样 metadata 的图片应用程序,比如权限,是无用的,因此浪费存储空间。更重要的成本是为了找到文件需要把文件的 metadata 从磁盘读到内存。对小规模不明显,但对数十亿图片和 PB 级别的数据,访问 metadata 是吞吐量的瓶颈。我们发现这是我们使用 NAS 的关键问题。需要一些磁盘操作来读取一个图片:一个(通常更多)用来转换文件名到 inode 号,另一个从磁盘读 inode,最后一个读文件本身。对 metadata 使用磁盘 IO 是我们读取吞吐量的限制因素。观察到实际上这个问题引入了一个额外的成本,我们需要依赖 CDN 比如 Akamai,来解决主要的读数据量
为此,我们设计 Haystack 来达到以下四个主要目的
高吞吐量和低延迟:我们的图片存储系统需要支撑用户的请求。超过我们处理容量的请求要么被忽略,这对用户体验来说是不可接受的,要么被 CDN 处理,其成本高且得到一个消失的返回。更进一步,图片需要快速提供来得到好的用户体验。Haystack 通过每次读取请求最多一次磁盘操作来获得高吞吐量和低延迟。我们通过保持所有 metadata 到内存来实现,我们戏剧化地缩减每图片 metadata 来找到磁盘上的文件
容错:在大规模扩展系统,故障每天都在发生。我们的用户的图片需要有效,即使在有不可避免的服务器崩溃和磁盘故障的情况下。有可能一整个数据中心失去电力或一个跨国连接服务。Haystack 复制每个图片到地理上不同的地区。如果我们失去了一台机器,我们引入另一台替代,必要时拷贝冗余数据
高效成本:Haystak 有更好地执行且比我们之前的 NFS 方案有更低的成本。我们用两个维度量化我们的节省成本:Haystack 有用存储的每 TB 成本和 Haystack 有用存储的每 TB 常规读速度。在 Haystack 中,每有用 TB 成本低 28% 且每秒处理超过 4 倍读速度相比之前的 NAS 应用程序
简单:在生产环境中我们不能夸大直接实现和维护的设计的能力。Haystack 是一个新系统,缺少生产线上多年的测试,我们特别关注于让它保持简单。简单使得我们能在几个月时间中开发一个工作系统而不是几年
这个工作描述了从概念到实现一个产品质量系统服务一天数十亿图片的 Haystack 的经验。我们的三个主要贡献是:
- Haystack,一个对象存储系统优化了高效地存储和提取数十亿图片
- 在构建和扩展一个不高昂,可靠和有效的图片存储系统上学到了一些经验教训
- Facebook 图片共享应用程序的请求特征
背景和之前的设计
在本章节中,我们描述之前的架构和我们学到的主要经验。由于篇幅限制,对之前设计的讨论省略了一些生产级开发的细节
背景
我们开始简介对 Web 服务器,CDN 和存储系统如何交互服务一个特殊网站的图片。下图描述了当一个用户访问一个包含图片的页面直到它从磁盘位置下载的步骤。当访问一个页面用户浏览器首先发送一个 HTTP 请求到一个 Web 服务器,浏览器收到响应进行渲染。对每个图片 Web 服务器构建一个 URL 来定位从哪里下载。对一个流行的网站这个 URL 通常指向一个 CDN。如果 CDN 有图片数据缓存则 CDN 立即响应数据。否则,CDN 检查 URL,其嵌入了足够的信息来从网站存储系统获取图片。CDN 然后更新它的缓存数据且发送图片到用户浏览器
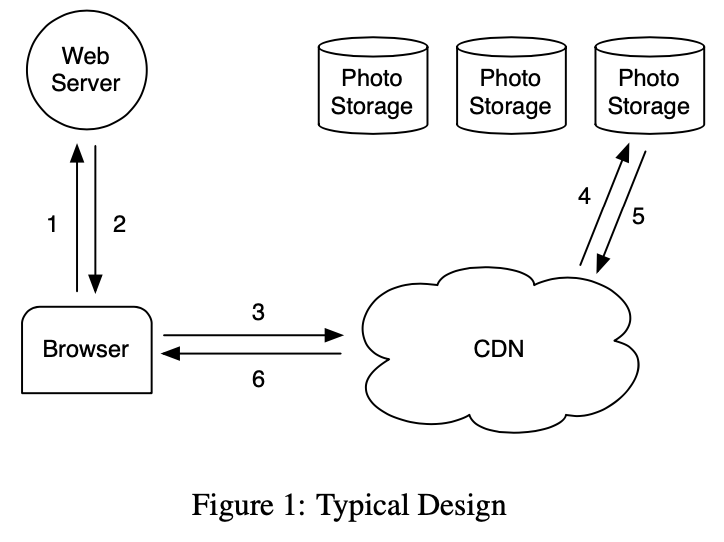
基于 NFS 的设计
在我们的首个设计中我们实现了使用一个基于 NFS 的图片存储系统。本节后续内容提供更多该设计的细节,主要的经验我们学到的是 CDN 本身不提供实际的解决方案供应一个社交网络网站的图片。CDN 高效供应最热点的图片 - 最近上传的图片 - 但一个社交网络网站比如 Facebook 也有大量请求对不那么热点的内容,我们称之为长尾。长尾请求是一个重要的流量,其请求 CDN 上缺失导致访问后台图片存储系统主机。把长尾所有图片缓存是一个非常方便的办法,但这需要非常大的缓存因此成本高
我们基于 NFS 的设计存储每个图片到一系列商业 NAS 应用程序里它自己的文件中。一系列机器,图片存储服务器,加载通过 NFS 的 NAS 应用程序导出的所有卷积。下图展示了这个架构且显示图片存储服务器处理图片的 HTTP 请求。从一个图片的 URL 中一个图片存储服务器提取卷积和全路径到文件,读取 NFS 数据且返回结果到 CDN
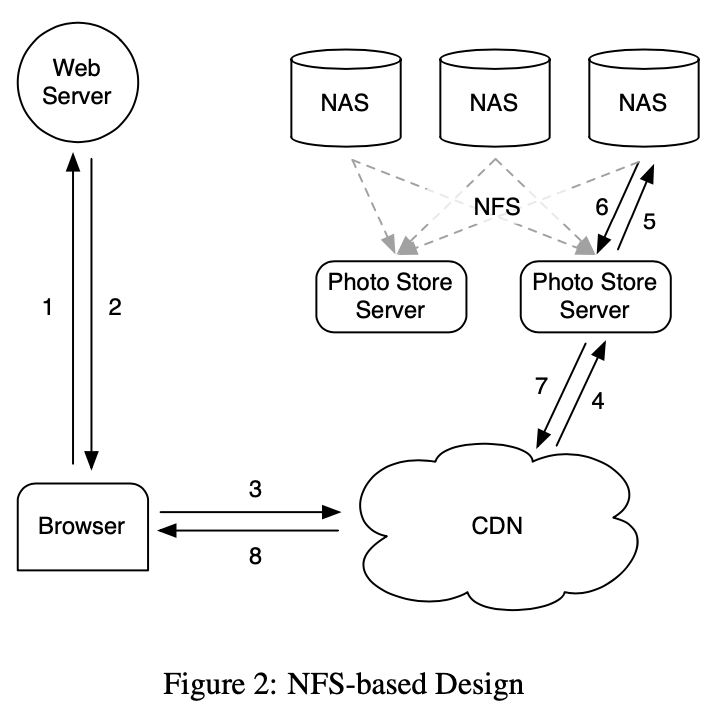
我们初始化在每个 NFS 卷目录中中存储数千个文件导致读取一个图片过多的磁盘操作。因为 NAS 应用如何管理目录 metadata,一个目录中放数千个文件非常低效因为目录的块 map 非常大而不能被应用有效缓存。这样它通常导致提取一个图片需要超过 10 次磁盘操作。在缩减目录大小到每目录数百个文件后,系统获取一个图片需要 3 次磁盘操作:一次读取目录 metadata 到内存,一次加载 inode 到内存,最后读取文件内容
为进一步减少磁盘操作我们让图片存储服务器直接缓存 NAS 应用返回的文件句柄。当第一次读取一个文件一个图片存储服务器正常打开文件但缓存文件名到文件句柄映射到内存缓存。当请求一个文件其文件句柄被缓存,一个图片存储服务器使用我们添加到内核的系统调用 open_by_filehandle 直接打开文件。遗憾的是,这个文件句柄缓存只提供一个镜像改进,不流行的图片开始不太会被缓存。一个可能的争论是所有文件句柄存储在 memcache 可能是一个可行的解决方案。然而,唯一有问题的部分它依赖 NAS 应用在内存有所有的 inode,这是对分布式系统一个高昂的需求。我们从这个 NAS 方案学到的是,对于缓存,是否 NAS 应用缓存或外部缓存如 memcache 对减少磁盘操作的影响有限。存储系统停止处理不流行图片的长尾需求,其不适合在 CDN 处理且容易在我们的缓存中不能命中
讨论
提供精确的指导什么时候构建或不构建自定义存储系统很困难。然而,我们相信对社区获得经验为什么我们决定构建 Haystack 是有帮助的
面对基于 NFS 设计的瓶颈,我们探讨是否构建一个类似 GFS 的文件系统是有用的。因为我们存储多数我们用户的数据在 MySQL 中,我们的系统中文件主要的使用是目录工程师用来开发工作,日志数据和图片。NAS 应用提供一个非常好的性价比对开发工作和日志数据。更进一步,我们杠杆 Hadoop 对极大地日志数据。服务长尾的图片请求呈现出了问题,它不适合 MySQL,NAS 应用和 Hadoop
我们面临的窘境是现有的存储系统缺乏好的内存磁盘比。然而,没有好的比率。系统需要足够的主存使得所有文件系统 metadata 都被缓存。在我们基于 NAS 的方案中,一个图片对应一个文件且每个文件需要至少一个 inode,一个 inode 是几百字节大小。足够内存方案成本太高。为达到一个高性价比,我们决定构建自定义存储系统缩减每图片文件系统 metadata 大小使得足够内存比购买更多 NAS 应用性价比更高
设计和实现
Facebook 使用一个 CDN 来获取流行图片且杠杆 Haystack 来高效响应长尾图片请求。当一个 Web 网站有一个 I/O 瓶颈提供静态内容,传统的解决方案是使用一个 CDN。CDN 负责主要的部分这样存储系统可处理剩下的长尾。在 Facebook 一个 CDN 需要缓存大量静态内容这样使得传统的存储系统不会达到 I/O 极限
理解到在不久的将来 CDN 将不能完全解决我们的问题,我们设计 Haystack 来解决我们基于 NFS 的方案的关键瓶颈:磁盘操作。我们接收可能请求磁盘操作的非流行图片的请求,但目标是限制这样操作的数量只为读取真正的数据。Haystack 通过戏剧化地缩减对文件系统 metadata 的内存使用来达到这个目标,因此实际上保持了所有 metadata 数据在内存中
回忆存储每文件单个图片导致更多的文件系统 metadata 被缓存。Haystack 使用一个直接的处理:它存储多个图片到一个文件且因此维护非常大的文件。我们显示这个直接处理是显著高效的。更多的, 我们认为它的简单性就是它的力量,能够快速实现和部署。我们现在讨论围绕它的核心技术和架构部件如何提供一个可靠有效的存储系统。在如下的 Haystack 描述中,我们区分两种 metadata。应用程序 metadata 描述浏览器需要用到提取图片的构建 URL 的信息。文件系统 metadata 确定一个主机获取主机磁盘上的图片的必要数据
概述
Haystack 架构包含 3 个核心部件:Haystack 存储,Haystack 目录和 Haystack 缓存。为简化我们省略前面的 Haystack。存储封装图片的持久化存储系统且是管理图片文件系统 metadata 的唯一部件。我们用物理卷组织存储的容量。例如,我们可组织一个服务器的 10 TB 容量为 100 个提供 100 GB 存储的物理卷。我们进一步分组不同机器的物理卷为逻辑卷。当 Haystack 存储一个图片到逻辑卷,图片被写入所有对应物理卷。这个冗余允许我们迁移由于硬盘故障,磁盘驱动器 Bug 等导致的数据丢失。目录管理逻辑到物理映射及其他应用程序 metadata,比如每个图片所在的逻辑卷和逻辑卷可用磁盘空间。缓存作为我们的内部 CDN,其保护对请求最流行图片的存储和提供上流 CDN 节点故障需要重新刷新内容的隔离设施
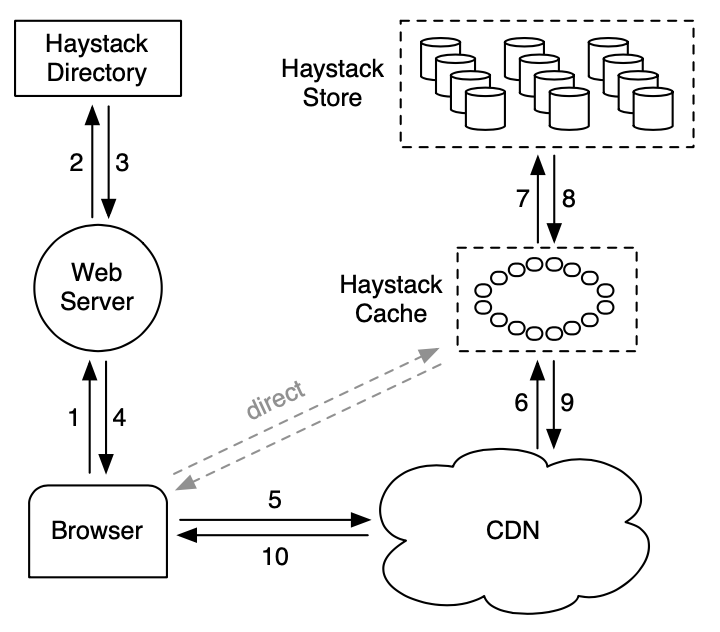
上图显示存储,目录和缓存部件如何在用户浏览器,Web 服务器,CDN 和存储系统中交互。在 Haystack 架构中浏览器可直接接触到 CDN 或者缓存。注意缓存是一个 CDN,为避免混淆,我们用 CDN 指代外部系统,缓存指向内部缓存图片的 CDN。一个内部缓存架构让我们减少对外部 CDN 的依赖
当一个用户访问一个网页 Web 服务器使用目录来对每个图片构建 URL。URL 包含一些信息,对应当用户浏览器联系 CDN(或缓存)带最终获取存储机器上的图片。一个典型的 URL 指导浏览器到 CDN 如下:
http://<CDN>/<Cache>/<Machine id>/<Logical volume, Photo>
URL 的第一部分指明向哪个 CDN 请求图片。CDN 可使用 URL 的后续部分内部查看图片:逻辑卷和图片 id。如果 CDN 不能定位图片则它从 URL 中获取 CDN 地址且联系缓存。缓存做类似地查找,当未命中,从 URL 中获取缓存地址且从指定存储机器上请求图片。图片请求直接到缓存有一个类似的工作流除了 URL 中的 CDN 说明信息
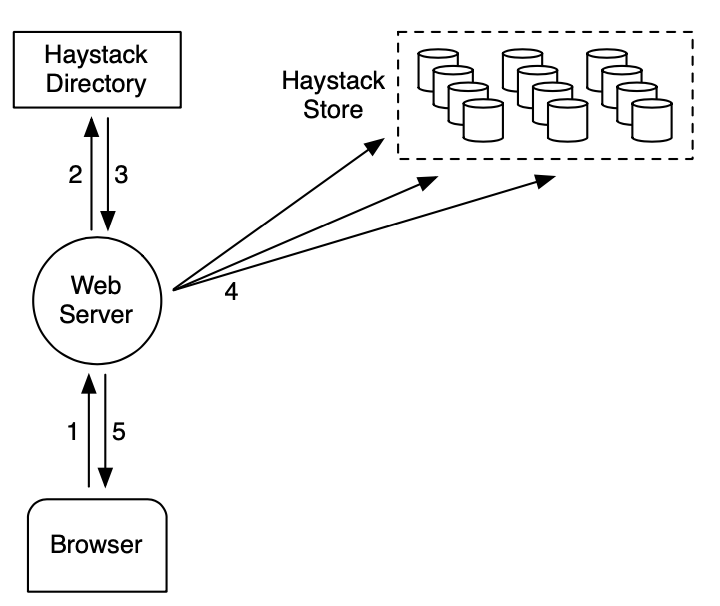
上图显示 Haystack 的上传路径。当用户上传一个图片时它首先发送数据到一个 Web 服务器。接下来,服务器从目录中请求一个可写的逻辑卷。最后,Web 服务器分配一个唯一的 id 给图片且上传到逻辑卷映射到的每个物理卷
Haystack 目录
目录提供四个主要功能。首先,他提供逻辑卷到物理卷的映射。Web 服务器使用这个映射上传图片和从一个页面请求中构建图片 URL。其次,目录负载平衡逻辑卷和物理卷的读。第三,目录确定是否一个图片请求应该被 CDN 处理还是被缓存。这个功能让我们调整对 CDN 的依赖。最后,目录确定那些逻辑卷是只读的或因为那些卷达到了存储上限。我们以机器粒度标签卷为只读这样操作更容易
当我们通过添加新的机器来扩展存储容量,这些机器为可写的;只可写的机器接收上传。这样这些机器有效的容量会下降。当一个机器耗光它的容量,我们标签它为只读。在下一小节中我们讨论这个区别如何对缓存和存储的影响
目录是个相对直接的部件通过一个 PHP 接口存储它的信息到一个复制数据库,该数据库平衡 memcache 来减少延时。当我们在一个存储机器上丢失数据的事件中我们移除映射中对应的条目且当新存储机器上线时替换它
Haystack 缓存
缓存接收从 CDN 过来或用户浏览器的 HTTP 图片请求。我们组织缓存为一个分布式 hash 表且使用一个图片 id 作为 key 来定位缓存数据。如果缓存不能立即响应请求,则缓存从 URL 中确定的存储机器获取图片且相应 CDN 或用户浏览器
我们现在高亮缓存的重要行为。它缓存一个图片当两个条件满足时:(a)请求直接来自用户而不是 CDN (b) 图片从一个可写存储机器获取。第一个条件的调整是我们对基于 NFS 设计的经验显示存储 CDN 缓存是低效的,因它不太可能当 CDN 未命中时会在我们内部缓存中找到。第二个的推理是间接的。我们使用缓存上架可写存储机器为读因为两个有趣的属性:图片一上传就会有最大的访问量且文件系统对只读只写的工作负载性能更好。这样可写存储机器可看到最多的读如果它不在缓存。给定这个特性,一个我们计划实现的优化是主动推最新上传的图片到缓存因为我们期望这些图片很快会被读取且访问量较大
Haystack 存储
存储机器的接口很基础。读是非常特别的且图片请求包含一个给定的 id,一个确定的逻辑卷和一个特别的物理存储机器。机器发现图片则返回。否则返回一个错误
每个存储机器管理多个物理卷。每卷有数百万个图片。读者可认为一个物理卷为一个非常大的文件(100 GB)存储为 ‘/hay/haystack_<logical volume id>‘。一个存储机器可使用逻辑卷对应的 id 和文件偏移快速访问一个图片。这是 Haystack 设计的关键:获取图片文件名,偏移和大小不需要磁盘操作。一个存储机器保持打开每个物理卷的文件句柄及图片 id 到文件系统 metadata 的内存映射(例如,文件,偏移和大小)
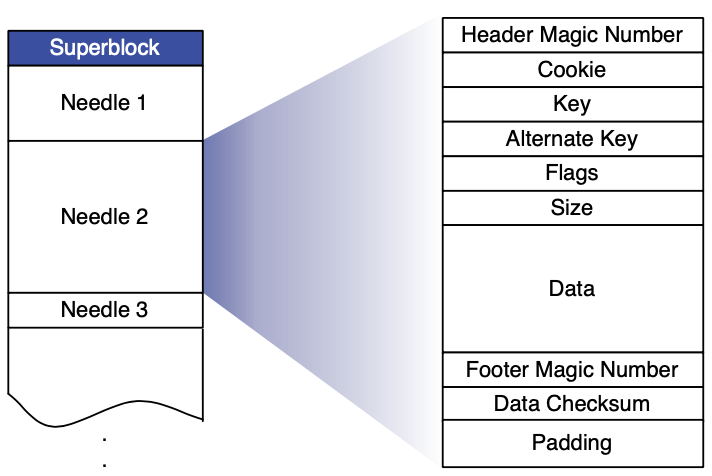
我们现在描述每个物理卷的布局和如何从内存映射到卷中。一个存储机器代表一个物理卷,作为一个大文件包含一个超级块及接着一系列 needle。每个 needle 代表 Haystack 中一个存储的图片。上图显示了一个卷文件和每个 needle 的格式。下表描述了每个 needle 中的各个字段
| 字段 | 解释 |
|---|---|
| Header | 魔数 |
| Cookie | 随机数用来缓和暴力查找 |
| Key | 64 位图片 id |
| Alternate key | 32 位辅助 id |
| Flags | 签证删除状态 |
| Size | 数据大小 |
| Data | 实际图片数据 |
| Footer | 恢复用魔数 |
| Data Checksum | 用来检查集成 |
| Padding | 用来做 8 字节对齐 |
为快速获取 needle,每个存储机器维护一个其卷的内存数据结构。该数据结构映射(Key, alternate Key)对到对应 needle 的标志位,大小和卷偏移。在一次崩溃后,一个存储机器在处理请求前可从卷中直接重建这个映射。我们现在描述一个存储机器如何维护它的卷和内存映射,响应读取、写入和删除请求(只有存储支持的操作)
-
读取图片
当一个缓存机器请求一个图片它支持存储机器的逻辑卷 id,key,alternate key 和 cookie。cookie 是嵌入在图片 URL 中的一个数。cookie 的值随机分配且在图片上传时存储在目录中。cookie 能有效地消除针对图片有效 URL 猜测的攻击
当一个存储机器从缓存机器接收到一个图片请求,存储机器在它的内存映射中查找相关 metadata。如果图片没有被删除存储机器查找卷文件中合适的偏移,从磁盘读取整个 needle(其大小可提前计算),且验证 cookie 和集成数据。如果这些检查通过则存储机器返回图片给缓存机器
-
写入图片
当上传图片到 Haystack 时 Web 服务器提供逻辑卷 id,key,alternate key,cookie 和 数据给存储机器。每个机器同步添加 needle 图片到它的物理卷文件且按需上传内存映射。这个只添加限制包含一些修改图片的操作比如旋转。Haystack 不允许覆盖 needle,图片只能通过添加一个更新的相同 key 和 alternate key 的 needle。如果新的 needle 写入到不同的逻辑卷,目录更新它的应用程序 metadata 和后续的请求将不会获取老版本。如果新的 needle 写入到相同的逻辑卷,则存储机器添加新的 needle 到对应相同的物理卷。Haystack 基于偏移区分这样重复的 needle。即最新版本的 needle 在物理卷中是最高偏移的那个
-
图片删除
删除图片是直接的。一个存储机器设置删除标志到内存映射和同步到卷文件中。请求删除的图片首先检查内存标志且如果标志被设置则返回错误。注意删除的 needle 空间被丢失了。之后,我们讨论如何通过压缩卷文件来获取删除 needle 的空间
-
Index 文件
存储机器重启的时候使用一个重要的优化 - index 文件。当理论上一个机器可通过读取所有它的物理卷来重构它的内存映射,这个操作是非常耗时的,因为所有的数据(TB 级别)需要从磁盘读取。Index 文件允许一个存储机器快速构建内存映射,减少重启时间
存储机器对每卷维护一个 index 文件。index 文件是内存数据结构的检查点用来高效定位磁盘的 needle。一个 index 文件的布局跟一个卷文件相似,包含一个超级块跟随一系列 index 记录对应超级块中每个 needle。这些记录必须跟 needle 在卷文件中的顺序保持一致。下图显示了 index 文件布局及下表解释了记录中每个字段
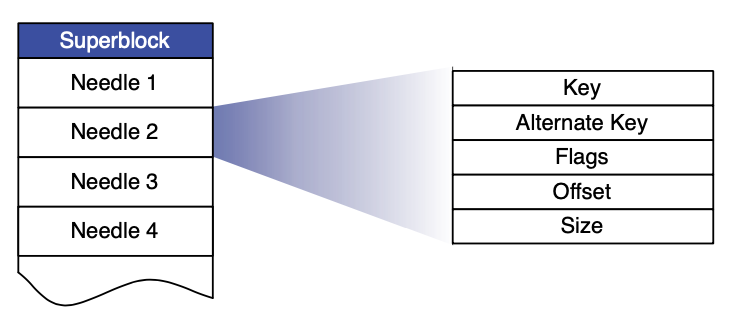
字段 解释 Key 64 位 key Alternate Key 32 位 alternate key Flags 当前未使用 Offset Haystack 存储中 needle 偏移 Size Needle 数据大小 重启使用 index 比读索引和初始化内存映射要更复杂。因为 index 文件是异步更新的,这意味着 index 文件可能有脏的检查点。当我们写一个新图片存储机器同步添加一个 needle 到卷文件的末尾且异步添加一个记录到 index 文件。当我们删除一个图片,存储机器同步设置图片 needle 的标志而不更新 index 文件。这些设计决定允许写和删除操作更快返回因为它们避免了额外的同步磁盘写。它们也造成两个影响我们得处理:needle 可能存在而没有对应的 index 记录和 index 记录不能反应删除文件
我们把没有对应 index 文件的 needle 称为孤儿。当重启时,一个存储机器顺序检查每个孤儿,创建一个匹配的 index 记录,且添加记录到 index 文件。注意我们可快速确定孤儿因为 index 文件中最后的记录对应卷文件中最后一个非孤儿。为完成重启,存储机器现在只使用 index 文件初始化它的内存映射
因为 index 记录不能反应删除文件,一个存储机器可提取一个事实上已删除的图片。为处理这个问题,在一个存储机器读取图片的整个 needle 之后,机器可检查删除标志。如果一个 needle 标志为删除存储机器更新它的内存映射且通知缓存对象未找到
-
文件系统
我们描述 Haystack 作为一个对象存储作为一个一般性类 Unix 文件系统,但一些文件系统比其他的更适合 Haystack。流行地,存储机器应该使用一个文件系统不需要太多内存来在一个大文件中快速执行随机查找。当前,每个存储机器使用 XFS,一个一定程度上的文件系统。XFS 对 Haystack 来说有两个主要优点。首先,对一些连续大文件的块映射可足够小来放入内存,其次,XFS 提供高效地文件预分配,缓和碎片和控制大块映射如何增长
使用 XFS,Haystack 可消除当读取一个图片时获取文件系统 metadata 的磁盘操作。但这不意味着 Haystack 可保证每个图片读取只发生一次磁盘操作。存在一些边界条件文件系统需要超过一次磁盘操作当图片跨边界或 RAID 边界时。Haystack 预分配 1 GB 大小且使用 256 kb RAID 条大小这样实际上这样的情况出现的很少见
故障恢复
跟许多其他运行在商业硬件上的大规模可扩展系统一样,Haystack 需要容忍各种故障:有缺陷的硬盘,行为异常的 RAID 控制器,有问题的主板等。我们使用两个直接的技术来容错 - 一个是检测,另一个是修复
为主动找到有问题的存储机器,我们维护一个后台任务,命名为 pitchfork,周期性检测每个存储机器的健康。Pitchfork 远程测试每个存储机器的连接,检查每个卷文件的有效性,尝试从存储机器上读数据。如果 pitchfork 确定一个存储机器一致性地未通过健康检测则 pitchfork 自动标记存储机器上的所有逻辑卷为只读。我们手动处理失败检测下线的原因
当诊断时,我们可快速修复问题。偶尔,一些情形需要大量繁重的同步操作,一个复制节点使用提供的卷文件重置存储机器的数据。这种情况很少发生(每月几次)且虽然慢但简单。主要的瓶颈在于同步的数据大于每个存储机器 NIC 卡的速度,导致恢复平均需要几小时。我们积极探索技术来处理这个限制
优化
我们现在讨论一些使 Haystack 成功的重要优化
-
紧致
紧致是一个在线操作重新获取删除和重复(key 和 alternate key 相同)的 needle 的空间。一个存储机器通过拷贝 needle 到一个新文件并忽略重复和删除的条目来紧致一个卷文件。在紧致期间,两个文件都会有删除。一旦这个过程达到文件的末尾,它阻塞对文件的修改且自动交换文件和内存结构
我们使用紧致来释放被删除图片的空间。删除的范式跟图片视图类似:新的图片更可能被删除。在一年的过程中,大约 25% 的图片被删除
-
节省更多内存
如描述所说,一个存储机器维护一个内存数据结构包括标志位,但我们当前的系统只使用标志位来标记 needle 为删除。我们去掉了对删除图片设置偏移为 0 的内存表示的需要。另外,存储机器不跟踪内存中的 cookie 值,在从磁盘读取一个 needle 之后不检测提供的 cookie。存储机器通过这两个技术缩减内存 20% 的使用
当前,Haystack 一般每图片使用 10 字节的内存。回忆我们扩展每个上传图片到 4 个图片其有相同的 key(64 位),不同的 alternate key(32 位)和一致的不同数据大小(16 位)。对这些 32 字节,Haystack 消费大约每图片 2 字节到 hash 表,使得对同一图片的 4 个扩展图片总共需要 40 字节。对比一下,考虑 Linux 中一个 xfs_inode_t 结构是 536 字节
-
批量上传
因为磁盘对大量顺序写的性能大于随机写,我们尽量批量更新。幸运地是,许多用户上传整个相册到 Facebook 而不是单个图片,提供一个明显的机会来批量相册图片。我们在后续章节会量化聚集写的改进
演化
我们划分我们的演化为四个部分。首先我们特征化 Facebook 的图片请求。第二和第三部分我们显示目录和缓存的高效。最后我们分析存储在合成和生产负载上的性能
特征化图片请求
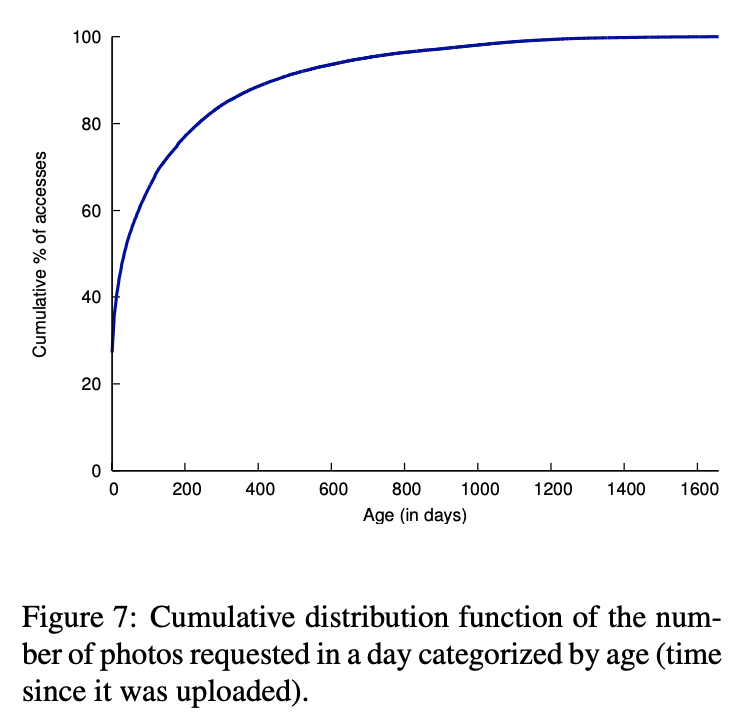
图片是 Facebook 用户分享的主要内容之一。用户每天上传数百万个图片且最新的图片比老图片更加流行。下图显示图片年龄和流行的关系。为理解图的形状,它可很好地用来讨论什么在驱动 Facebook 的图片请求
-
驱动图片请求的特征
两个特征对应 98% 的 Facebook 图片请求:新闻流和相册。新闻流特征显示朋友分享的最新内容。相册特征让用户浏览他朋友的图片。用户可观看最新上传的图片和浏览所有的个人相册
上图显示一个图片请求在几天内有一个凸起的上升。新闻流驱动多数的流量在最新的图片且 2 天后凸起下降明显当许多故事停止显示在缺省的流中。图中有两个高亮关键点。首先,流行度的快速下降建议 CDN 和缓存中的缓存对流行的内容非常高效。其次,图片有一个长尾表示大量请求不能适用缓存数据来处理
-
流量容量
操作 每日统计 图片上传 ~1.2 亿 Haystack 写图片 ~14.4 亿 图片被观看 800 - 1000 亿 [缩微图] 10.2% [小图片] 84.4% [中图片] 0.2% [大图片] 5.2% Haystack 图片读取 100 亿 上表显示 Facebook 图片流量。Haystack 写图片数是上传图片数的 12 倍,因我们的应用程序缩放每个图片为 4 种大小且保存到 3 个不同的位置。表中显示 Haystack 对应 CDN 大约 10% 的图片请求。观察到小图片被最多浏览。这个特征强调我们想要最小化 metadata 过载这样效率能很快提升。另外,读小图片对 Facebook 来说是延迟更敏感的操作因为它们显示在新闻流中而大图片显示在相册且可预取来隐藏延时
Haystack 目录
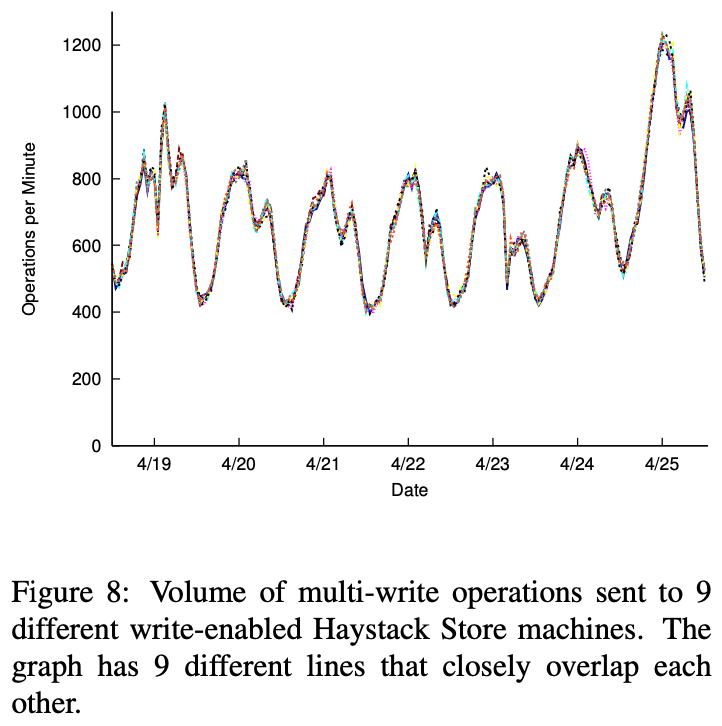
Haystack 目录平衡 Haystack 存储机器之间读和写。上图描述了目录的直接哈希策略对分布式读和写是非常高效的。上图显示 9 个同时进入生产线的不同存储机器的多写操作数量。每个这样的盒子存储不同的图片集。因为线几乎没有区别,我们认为目录平衡写效果很好。比较存储机器的读流量显示相似的平衡行为
Haystack 缓存
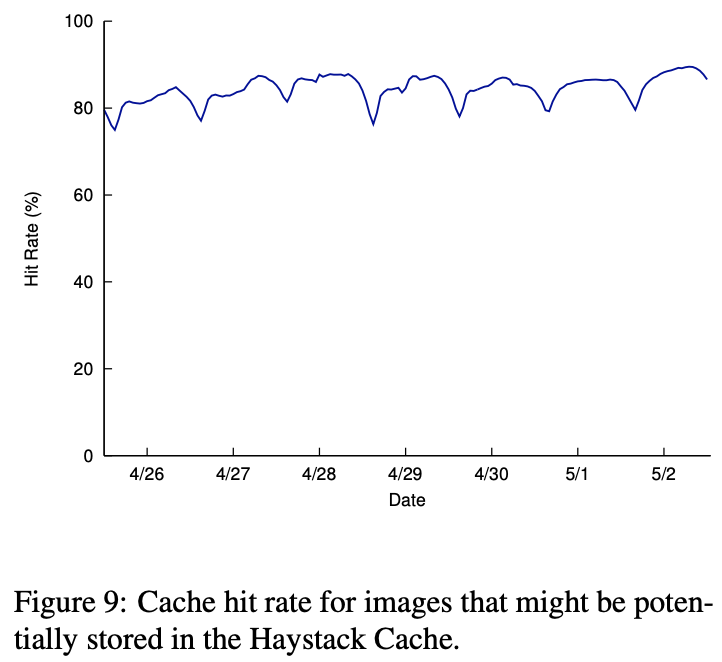
上图显示 Haystack 缓存命中率。回忆缓存只存储保存在可写存储机器上的图片。这些图片较新,这解释了大约 80% 的高命中率。因为可写存储机器也能看到最大数量的读,缓存高效地缩减机器的读请求率
Haystack 存储
回忆 Haystack 目标是长尾图片请求且目标为维护高吞吐和低延迟尽管是随机读。我们呈现在合成和生产负载的存储机器性能结果
-
实验的构建
我们采用商业存储刀片机作为存储机器。典型硬件配置的 2U 存储刀片机有 2 个超线程 4 核 Intel Xeon CPU,48 GB 内存,一个 256-512 MB NVRAM 的硬件 raid 控制器和 12 个 1 TB SATA 硬盘
每个存储刀片机提供大约 9 TB 容量,通过硬件 RAID 控制器配置一个 RAID-6 分区。RAID-6 在降低存储成本时提供适配的冗余和优异的读性能。控制器的 NVRAM 回写缓存缓冲 RAID-6 缩减写性能。因为我们的经验建议在存储机器上缓存图片是低效的,我们完全保留 NVRAM 用来写。我们也禁止磁盘缓存来保证当崩溃和电力丢失时的数据一致性
-
评测性能
我们使用两个评测评估存储机器的性能:Randomio 和 Haystress。Randomio 是一个开源多线程磁盘 I/O 程序,我们用来测量存储设备的裸能力。它随机读 64 KB 使用直接 I/O 来对齐扇区请求和报道最大维持吞吐。我们使用 Randomio 来确立读吞吐的基线,我们可跟我们其他的评测比较结果
Haystress 是一个自定义构建多线程程序,我们用来评估存储机器的各种合成负载。它通过 HTTP 通信存储机器且访问存储机器可维持的最大读和写吞吐。Haystress 处理大量图片的随机读来缩减机器缓存 buffer 缓存的影响。即,几乎所有的读都需要一个磁盘操作。在本文中,我们使用 7 个不同的 Haystress 负载来评估存储机器
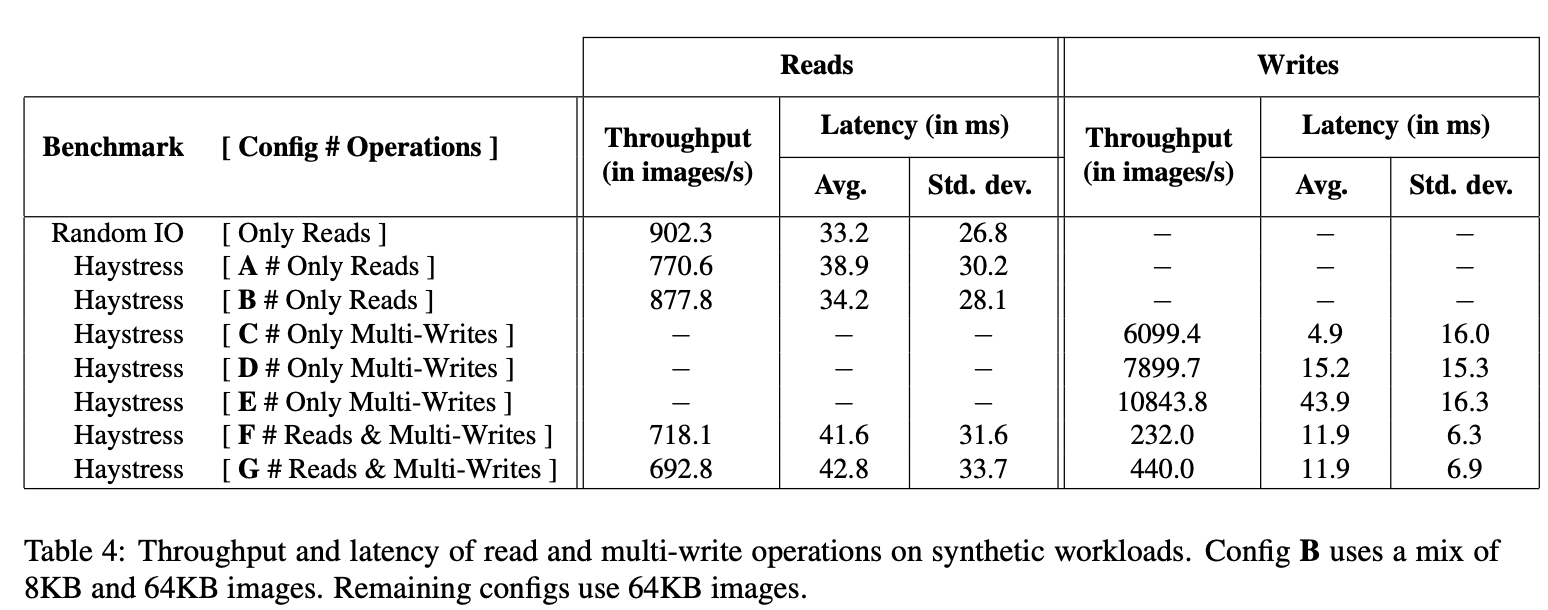
上图展示存储机器在我们的评测上能维持的读和写吞吐和相关延时。负载 A 执行对有 201 卷的存储机器 64 KB 图片的随机读。结果显示 Haystack 转发 85% 的设备裸吞吐而只有 17% 有更高的延时
我们确立存储机器的开支有 4 个因素:(a) 它运行在文件系统之上而不是直接访问磁盘 (b) 超过 64 KB 的磁盘读作为整个 needle 需要读 (c) 存储的图片可不对齐 RAID-6 设备条大小这样一个小比例的图片会从多个磁盘读且 (d) Haystack 服务器 CPU 开支(索引访问,checksum 计算等)
在负载 B 我们又检查一个只读负载但修改 70% 的读这样它们请求更小尺寸的图片(8 KB 而不是 64 KB)。实际上,我们发现大多数请求的不是最大尺寸图片而是图标和配件图片
负载 C,D 和 E 显示一个存储机器的写吞吐。回忆 Haystack 可批量写。负载 C,D 和 E 的第 1,4 和 16 组分别写为一个单独的多写。该表显示在 4 个和 16 个图片写的吞吐摊还固定成本分布改进了 30% 和 78%。如期望的,这减少了图片延迟
最后,我们看读写操作的性能。负载 F 使用一个混合 98% 的读和 2% 的多写,负载 G 使用一个混合 96% 的读和 4% 的多写,每个多写写 16 个图片。这些比例经常在生产环境中观测到。该表显示在写的同时展现了存储转发高吞吐
-
生产负载
本节检测生产机器存储的性能。有两类经典的存储 - 写启动和只读。写启动主机服务读和写请求。只读主机服务只服务读请求。因为这两类有不同的流量特征,我们每类分析一组机器。所有机器有相同的硬件配置
以秒为粒度,一个存储盒的图片读写操作中可看到巨大的峰值。为确保即使在峰值处也有合理的延迟,我们保守地分配大量写启动机器这样它们平均使用率降低
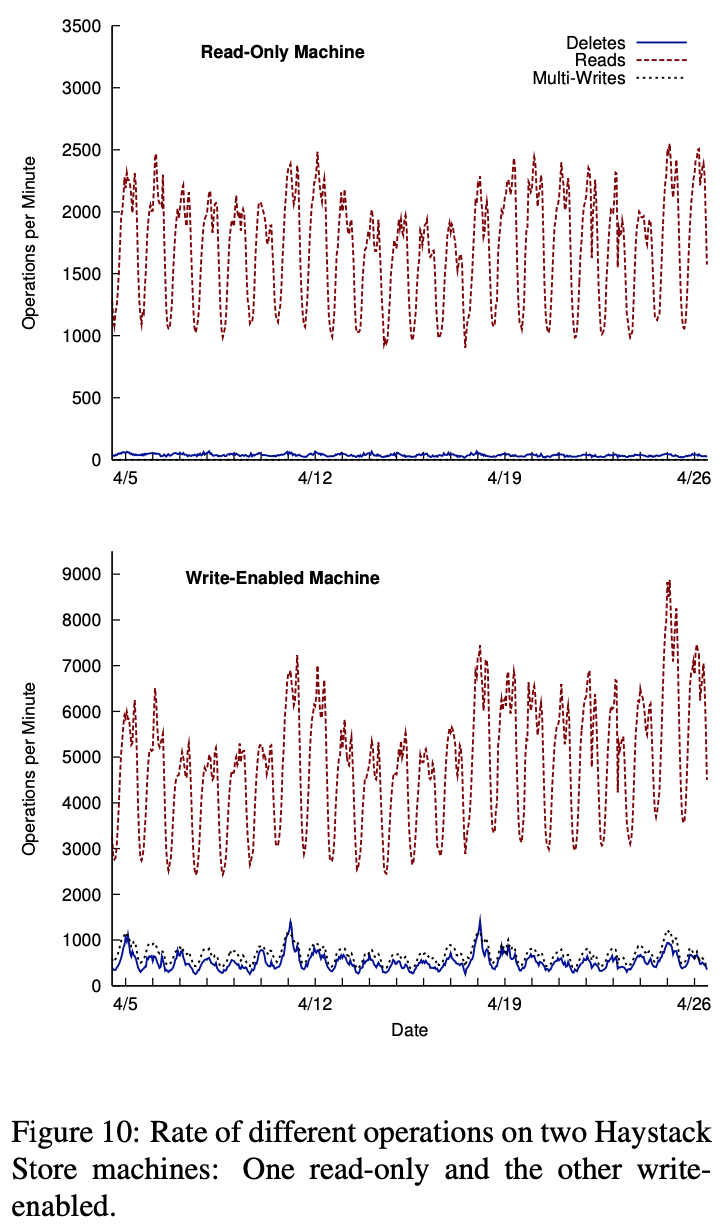
上图显示在只读和写启动存储机器上不同类型操作的频率。注意我们看到周日和周一是图片上传峰值,其次是周四到周六。一般我们对环境的影响每天增长 0.2% 到 0.5%
在生产机器上写存储总是多写来摊分写操作固定成本。找到图片组是很直接的因为每个图片的 4 种不同大小都存储在 Haystack。对用户也说上传一批图片到图片相册也是常见的。组合这两个因素,对这个写启动机器的每多写平均图片数量是 9.27
之前章节解释了对最近上传的图片和丢弃读和删除速率很高。这个行为也在之前的表上能观测到。写启动盒看到更多的请求(甚至一些读流量在缓存中已处理)
另一个值得记录的趋势是:当更多的数据写入写启动盒使得卷中图片增加,导致读速度增加
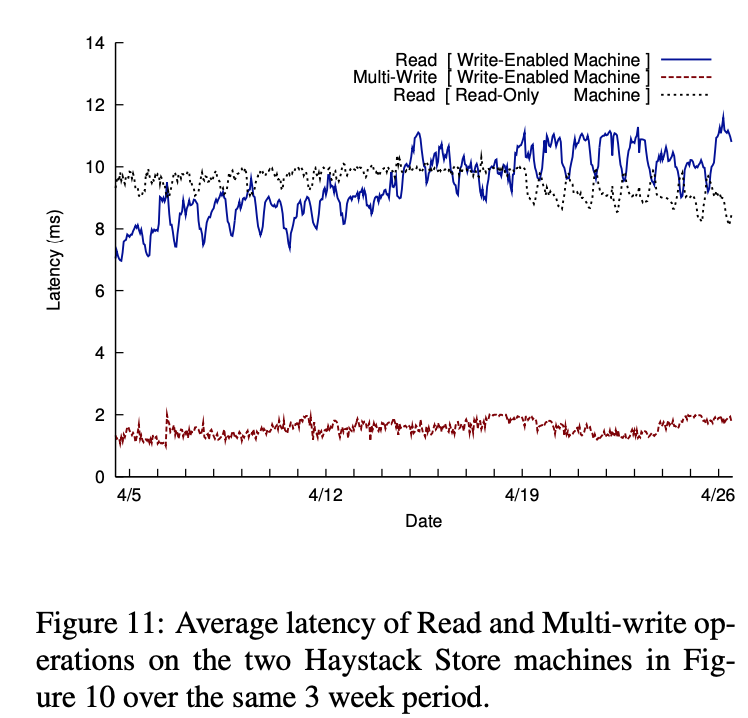
上图显示和上上图相同周期内在相同的两个机器上读和多写操作的延时
多写操作的延时相当低(在 1 到 2 微秒之间)且当卷流量产生巨大变动时也很稳定。Haystack 机器有一个基于 NVRAM 的 raid 控制器。NVRAM 允许写跳针异步且当多写完成时处理一个单同步来刷新卷文件。多写延时非常平滑和稳定
在只读盒上读延时也相当稳定即使在卷流量巨大变化时(3 周周期的 3 倍)。对一个写启动盒读性能被三个主要因素影响。首先,当存储在机器上的图片数量增长,机器的读流量也增长(比较前图的周流量)。其次,在写启动机器上的图片被缓存而在只读机器上的不会缓存。这表明只读机器的缓存区更高效。第三,因为 Facebook 高亮最近的内容最近写的图片通常会立即被读取。这样的读在写启动机器上总是在缓存中命中且改进了缓存命中率。上图的线图形是组合了这三个因素的结果
存储机器上 CPU 利用率很低。CPU 空闲时间在 92-96% 之间
相关工作
如我们所知,Haystack 目标是一个新的设计点聚焦于大型社交网络网站的长尾图片请求。
文件系统
Haystack 使用 Rosenblum 和 Ousterhout 设计的日志结构文件系统,其基于大多数读可被缓存处理的思想优化写吞吐。图片被添加到 Haystack 存储和开启写启动的机器的 Haystack 缓存。关键的不同之处是(a)Haystack 存储机器用这种方式写使得它们变成只读时对读操作非常高效(b)随时间推移对更老的数据读请求减少
一些工作被提出如何高效管理小文件和 metadata。通常的处理是如何有效地分组相关文件和 metadata。Haystack 避免了这些问题因为它在内存中维护 metadata 且用户通常成批次上传图片
基于对象的存储
Haystack 的架构共享了许多跟 Gibson 在网络安全磁盘(NASD)的对象存储系统论文中的相似处。Haystack 目录和存储也许跟文件和存储管理概念最相似,在 NASD 中从物理上分离了逻辑存储单元。在 Wang 的 OBFS 中,构建一个用户水平的对象存储系统是 XFS 的 1/25 大小。虽然 OBFS 比 XFS 有更大的写吞吐,它的读吞吐(Haystack 的主要担忧点)明显更糟
管理 metadata
Weil 在一个 PB 级别对象存储 Ceph 中处理扩展 metadata 管理。Caph 通过引入生成函数而不是直接的映射来分离逻辑单元到物理单元的映射。客户端可计算适合的 metadata 而不是通过查找。在 Haystack 中实现这个技术对对象存储更低效因为相比对象,且被一个唯一的数值确定,缺少目录间接引入的语义分组。他们的解决方案是嵌入内部对象关系到对象 ID 中。这个想法跟 Haystack 正交因为 Facebook 直接存储这些语义关系作为社交图的一部分。在 Spyglass Leung 中提议一个对大型存储系统中 metadata 进行快速可扩展的查询设计。Manber 和 Wu 也提议在 GLIMPSE 中对整个文件系统进行查找。Patil 使用一个 GIGA+ 中的复杂算法来管理每目录数十亿文件的 metadata。我们在工程中使用了一个更简单的解决方案,Haystack 不提供查找特性也不提供传统 Unix 文件系统的语义
分布式文件系统
Haystack 标记逻辑卷跟 Petal 中 Lee 和 Thekkath 的虚拟盘相似。Boxwood 工程探索了使用高层数据结构作为存储的基础。当强制使用更复杂的算法,类似 B 树的抽象可能在 Haystack 意图倾向接口和语义时没有很大的影响。相似的,Sinfonia 的 mini-transactions 和 PNUTS 的数据库功能提供更多的特性和 Haystack 需要的更强地保证。Ghemawat 设计的 GFS 支持添加操作和大序列的读的负载。Bigtable 提供一个结构化数据的存储系统和跟数据库相似的特性来支持许多谷歌的项目。不清楚是否这些特性对图片存储的系统优化有作用
结论
本文描述了 Haystack,一个设计用于 Facebook 图片应用程序的对象存储系统。我们设计 Haystack 来服务在巨型社交网络中共享图片的长尾请求。关键点在于当访问 metadata 时避免磁盘操作。Haystack 提供一个容错和简单的解决方案,使得图片存储的成本戏剧性的降低和比使用 NAS 应用程序的传统处理更高的吞吐。更进一步,Haystack 增加了可扩展性,提供每周用户上传数千万图片的必要质量保证
Share
定义 一个序为 n 的二进制 De Bruijn 序列是一串位字符串 $ b_ {i} \in \{0, 1\}, b = \{b_ {1}, \ldots, b_ {2^{n}}\} $ 使得每个长度为 n 的连续子串 $ \{a_ {1}, \ldots, a_ {n} \} \in \{0,1\}^{n} $ 在 b 中只出现一次(即 $ \exists !k $ 使得 $ b_ {k} = a_ {1}, b_ {k+1} = a_ {2}, \ldots, b_ {k+n-1} = a_ {n} $,索引对 $ 2^{n} $ 取模
例2 一个序为 3 的 De Bruijn 序列为 00010111
我们可检查所有可能的长度为 3 的子串在这个序列中仅出现一次。同样,可证明对任意n,序为 n 的 De Bruijn 序列存在。我们将用一个定理简单陈述,但之前我们首先检查 De Bruijn 图的定义,它在我们的证明中扮演关键的角色
定义 一个 De Bruijn 图是一个有向图 $ DB_ {n} = (\{0, 1\}^{n-1}, \{0, 1\}^{n}) $,一个带 $ \{0, 1\}^{n-1} $ 个顶点的集合和一个 $ \{0, 1\}^{n} $ 边的集合,一条边从 $ a = \{a_ {1}, \ldots, a_ {n-1} \} $ 到 $ a^{\prime} = \{ a^{\prime}_ {1}, \ldots, a^{\prime}_ {n-1} \} $ 当且仅当
$ a_ {2} = a^{\prime}_ {1}, a_ {3} = a^{\prime}_ {2}, \ldots, a_ {n-1} = a^{\prime}_ {n-2} $
这相当于说有一条从 a 到 $ a^{\prime} $ 的边当且仅当 a 是一些字符串 $ b_ {1} \ldots b_ {n} $ 的前缀且 $ a^{\prime} $ 是相同字符串的一个后缀
例4 $ DB_ {3} $ 的图是
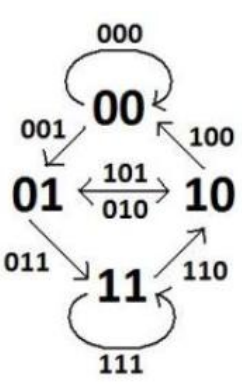
定理5 对任意 n,存在序为 n 的二进制 De Bruijn 序列,且有 $ 2^{2^{n-1}} $ 个
证明:为开始我们的证明我们注意到一个序为 n 的 De Bruijn 序列是一个 $ DB_ {n} $ 的欧拉环路。我们首先希望证明一个欧拉环路存在。为此我们注意到 $ DB_ {n} $ 是平衡的。这是因为我们可选取任意 n - 1 长的序列且删除最后一个数字,然后在前面添加一个 0 或 1,对每个顶点有 indeg = 2。相似地,我们可选取 n - 1 长度的任意序列且删除第一个数字,则添加一个 0 或 1 到最后,对每个顶点有 outdeg = 2。因为 indeg = outdeg = 2 所以我们的图是平衡的。当一个图是平衡的则一个欧拉环路存在,则我们知道对所有的 n 存在一个序为 n 的二进制 De Bruijn 序列
现在我们已证明 De Bruijn 序列的存在我们想要证明它们的遍历。从 $ DB_ {n} $ 的欧拉环路和 De Bruijn 序列对等及组合图论的结果我们有
$ \begin{aligned} \#\{DB_ {n} \} &= \#\{\text{Eulerian Tours of } DB_ {n}\} \\ &= \sum_ {e \in E}\tau(DB_ {n}, e) \\ &= \sum_ {e \in E}\kappa(DB_ {n}, e) \prod_ {v \in V}(outdeg(v) - 1)! \\ &= \sum_ {e \in E}\kappa(DB_ {n}, e) \end{aligned} $
最后的等式说明事实上图的每一个顶点有 outdeg = 2。然后我们想要统计捆绑到对应序为 De Bruijn 序列的 $ DB_ {n} $ 伸展树的数量。我们使用一个特别的技巧。考虑 $ DB_ {n} $中任意两个顶点 v 和 w 且统计在 v 和 w 之间路径长度为 n-1 的路径数。特别地设
$ v = (v_ {1}, \ldots, v_ {n-1}) $
$ w = (w_ {1}, \ldots, w_ {n-1}) $
这里只有一个方法来添加到我们的两个序列。特别地我们必须这样做:
$ \begin{array}{c} \left(v_{1} \ldots v_{n-1}\right) w_{1} \ldots w_{n-1} \\ \left(v_{1}\left(v_{2} \ldots w_{1}\right) w_{2} \ldots w_{n-1}\right. \\ v_{1} v_{2}\left(v_{3} \ldots w_{2}\right) w_{3} \ldots w_{n-1} \\ \vdots \\ v_{1} \ldots v_{n-1}\left(w_{1} \ldots w_{n-1}\right)\end{array} $
对所有顶点 v, w,因为我们只有一个长度为 n-1 从 v 到 w 的路径,我们有
$ A^{n-1} = \left( \begin{array}{ccc} 1 & \cdots & 1 \\ \vdots & \ddots & \vdots \\ 1 & \cdots & 1 \end{array} \right) $
A 是 $ DB_ {n} $ 的 $ 2^{n-1} \times 2^{n-1} $ 临接矩阵
我们应该看到这个拉普拉斯矩阵有特征值 0,当用 $ 2^{n-1} $ 乘以 1 和 2 时
最后我们应用矩阵树理论来获得结果:
$ \begin{aligned} \#\{DB \text{ sequences of order n} \} &= \sum_ {e \in E}\kappa(DB_ {n}, e) \\ &= \sum_ {e \in E} \frac{\lambda_ {1} \ldots \lambda_ {(2^{n-1} - 1)}}{2^{n-1}} \\ &= \sum_ {e \in E} \frac{2^{2^{n-1}-1}}{2^{n-1}} \\ &= 2^{n} \frac{2^{2^{n-1} - 1}}{2^{n-1}} \end{aligned} $
标注 可记录 De Bruijn 序列的数量为
$ 2^{2^{n-1}} = \sqrt{2^{2^{n}}} $
$ 2^{2^{n}} $ 为长度为 $ 2^{n} $的所有可能位字符串数量。这导致如果有一个双射:
$ \{\text{pairs of DB sequences of order n}\} \leftrightarrow \{\text{all binary bitstrings of length } 2^{n} \} $
这个证实是成立的,这样 De Bruijn 序列的讨论就结束了