Table of Contents
Algorithm
Course Schedule: https://leetcode.com/problems/course-schedule/
https://dreamume.medium.com/leetcode-207-course-schedule-1c4801ea7e76
Review
攻克视频技术 李江
基本概念:从参数的角度看视频图像
视频行业常见的分辨率有 QCIF(176 x 144)、CIF(352 x 288)、D1(704 x 576 或 720 x 576)、还有我们比较熟悉的 360P(640 x 360)、720P(1280 x 720)、1080P(1920 x 1080)、4K(3840 x 2160)、8K(7680 x 4320) 等
Stride 也可以称之为跨距,是图像存储的时候有的一个概念。它指的是图形存储时内存中每行像素所占用的空间。字节对齐引起的概念。比如要 16 字节对齐,则可能没行最后有一些多余的填充字节
帧率 一般帧率达到 10 ~ 12 帧每秒,人眼就会认为是流畅的。当然,可能会有个体差异
通常,我们在电影院看的电影帧率一般是 24fps,监控行业常用 25fps,声网常用的帧率有 15fps、24fps、30fps
码率 指视频在单位时间内的数据量的大小,一般是 1 秒内的数据量,单位一般是 Kb/s 或 Mb/s。
YUV & RGB
YUV 存储方式主要分为两大类:Planar 和 Packed 两种。Planar 格式的 YUV 是先连续存储所有像素点的 Y,然后接着存储所有像素点的 U,之后再存储所有像素点的 V,也可以是Y、V、U的顺序。Packed 格式的 YUV 是先存储完所有像素的 Y,然后 U、V 连续的交错存储
-
YUV 4:4:4
每一个 Y 对应有一个 U、V
-
YUV 4:2:2
每左右两个像素的 Y 共用一个 U、V。存储方式主要有以下 4 种类型:
-
YU16(或者称为 I422、YUV422P)
该类型是 Planar 格式,顺序为 Y、U、V
-
YV16(YUV422P)
该类型是 Planar 格式,顺序为 Y、V、U
-
NV16(YUV422SP)
Packed 格式,顺序为 Y、U、V
-
NV61(YUV422SP)
Packed 格式,顺序为 Y、V、U
-
-
YUV 4:2:0
这是最常见也是最常用的 YUV 类型。每上、下、左、右 4 个像素点共用一个 U 和一个 V,存储方式主要分为以下 4 种:
-
YU12(I420、YUV420P)
Planar 格式,顺序为 Y、U、V
-
YV12(YUV420P)
Planar 格式,顺序为 Y、V、U
-
NV12(YUV420SP)
Packed 格式,存储完 Y 之后,U、V 连续交错存储
-
NV21(YUV420SP)
Packed 格式,存储完 Y 之后,V、U 连续交错存储
-
RGB 和 YUV 之间的转换
Color Range 对一个 8bit 的 RGB 图像,每个 R、G、B 分量取值分两种,一种是 Full Range,一种是 Limited Range。Full Range 的 R、G、B 取值范围都是 0 ~ 255。而 Limited Range 的 R、G、B 取值范围是 16 ~ 235
YUV 和 RGB 转换的标准主要是 BT601 和 BT709(其实还有 BT2020)。简单来讲,BT709 和 BT601 定义了一个 RGB 和 YUV 互换的标准规范。BT601 是表情包的标准,而 BT709 是高清的标准
下面我们来看看这两种标准分别在 Full Range 和 Limited Range 下的 RGB 和 YUV 之间的转换公式

在处理 YUV 图像的存储和读取的时候,也是有 Stride 这个概念的。事实上,YUV 出问题的情况更多
缩放算法:如何高质量地缩放图像
最常用的是插值算法和目前比较火的 AI 超分算法
插值算法的原理都是使用周围已有的像素值通过一定的加权运算得到“插值像素值“。插值算法主要包括:最近邻插值算法(Nearest)、双线性插值算法(Billinear)、双三次插值算法(BiCubic)等
缩放的基本原理
图像的缩放就是将原图像的已有像素经过加权运算得到目标图像的目标像素
假设原图像的分辨率是 w0 x h0,我们需要缩放到 w1 x h1。那我们只需要将目标图像中的像素位置(x, y)映射到原图像的(x * w0 / w1,y * h0 / h1),再插值得到这个像素值就可以了,这个插值得到的像素值就是目标图像像素点(x,y)的像素值
三种插值算法
-
最近邻插值
- 首先,将目标图像中的目标像素位置,映射到原图像的映射位置
- 然后,找到原图像中映射位置周围的 4 个像素
- 最后,取离映射位置最近的像素点的像素做为目标像素
-
双线性插值
也取待插值像素周围的 4 个像素,将这 4 个像素值通过一定的运算得到最后的插值像素
线性插值原理是一种以距离作为权重的插值方式,距离越近权重越大,距离越远权重越小
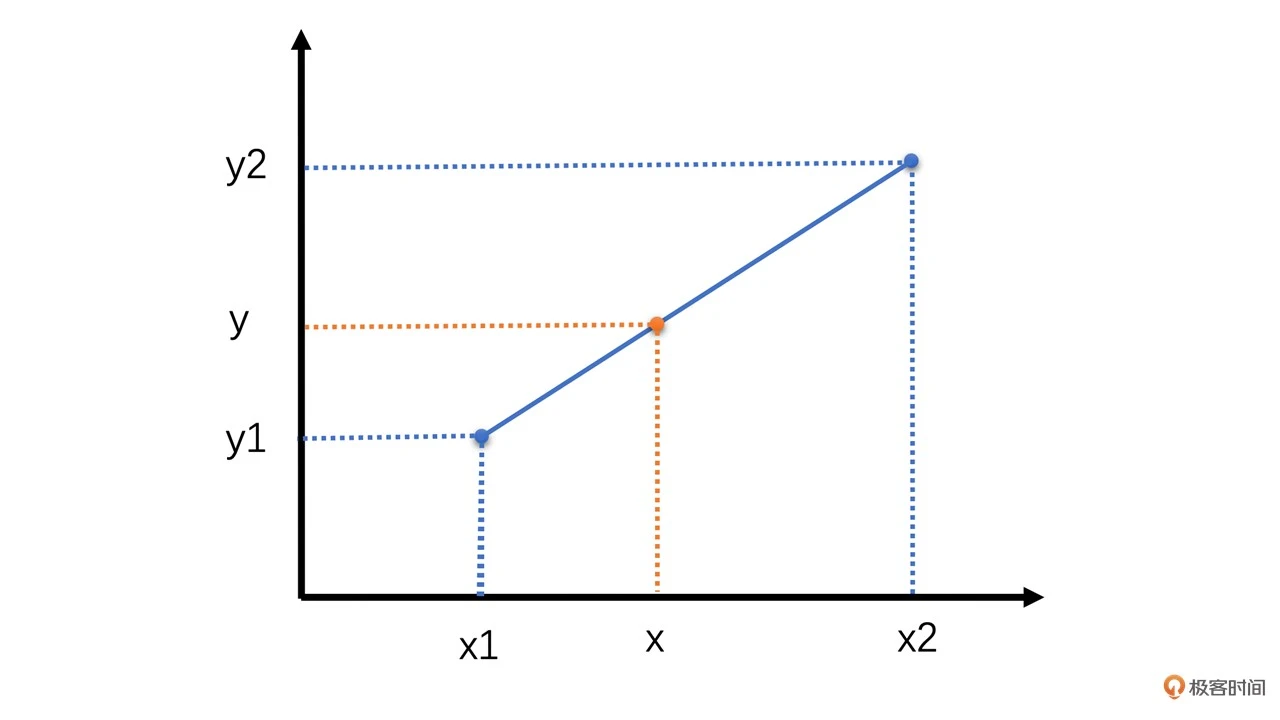
如上图,已知(x1, y1)和(x2, y2)两点,根据 x 值求对应的 y 值:
$ y = \frac{x_ {2} - x}{x_ {2} - x_ {1}} y_ {1} + \frac{x - x_ {1}}{x_ {2} - x_ {1}} y_ {2} $
双线性插值本质上就是在两个方向上做线性插值,双线性插值其实就是三次线性插值的过程,我们先通过两次线性插值得到两个中间值,然后再通过对这两个中间值进行一次插值得到最终的结果,如下图所示
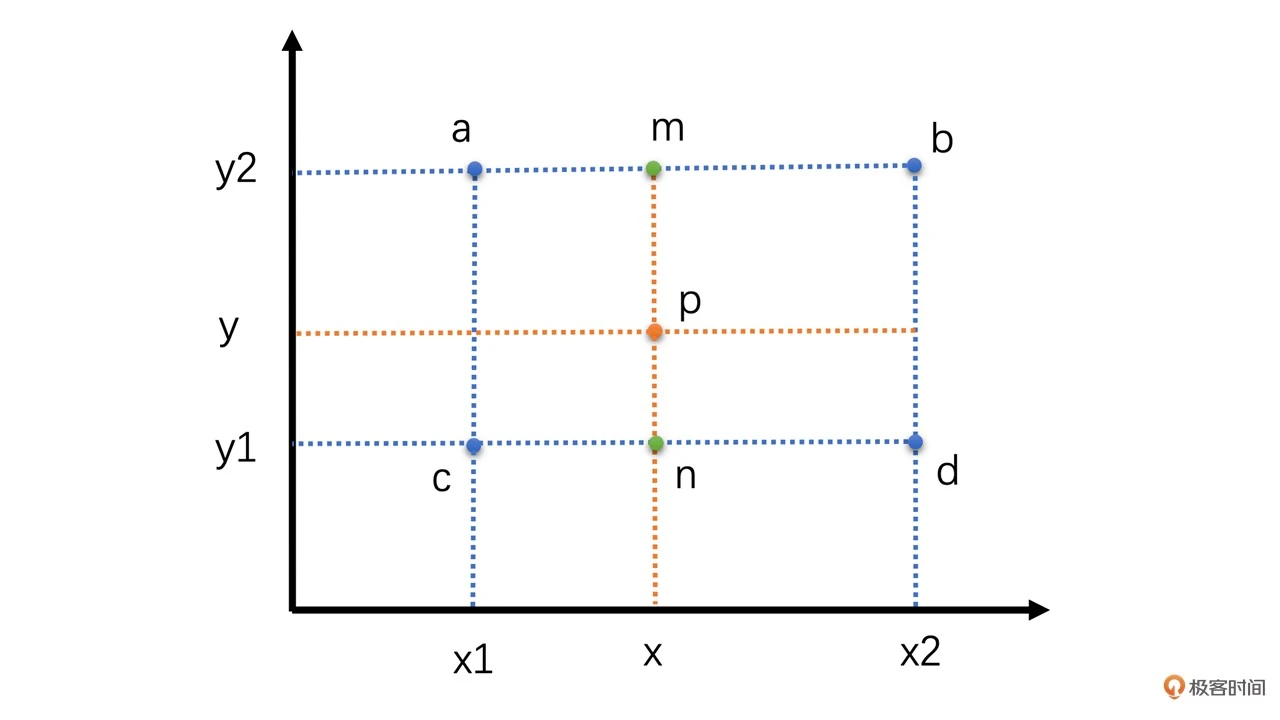
假设我们要插值求的是 p 点,其坐标为(x, y)。已知周围 4 个像素为 a、b、c、d。我们先通过 a 和 b 水平线性插值求得 m,再通过 c、d 水平插值求得 n。有了 m 和 n之后,再通过 m、n 垂直插值得 p 点的像素值。计算过程如下
$ val(m) = \frac{x - x_ {1}}{x_ {2} - x_ {1}} val(b) + \frac{x_ {2} - x}{x_ {2} - x_ {1}} val(a) $
$ val(n) = \frac{x - x_ {1}}{x_ {2} - x_ {1}} val(d) + \frac{x_ {2} - x}{x_ {2} - x_ {1}} val(c) $
$ val(p) = \frac{y - y_ {1}}{y_ {2} - y_ {1}} val(m) + \frac{y_ {2} - y}{y_ {2} - y_ {1}} val(n) $
-
双三次插值
双三次插值原理跟前面两种差不多,不同的是:
- 双三次插值选取的是周围 16 个像素,比前两种插值算法多了 3 倍
- 双三次插值算法的周围像素的权重计算是使用一个特殊的 BiCubic 基函数来计算的
先通过 BiCubic 基函数计算得到 16 个像素的权重,然后将 16 个像素加权平均就得到最终的插值像素
BiCubic 基函数形式如下
$ W(x) = \left\{ \begin{array}{cc} (a + 2) | x |^{3} - (a + 3) | x |^{2} + 1 & | x | \le 1 \\ a | x |^{3} - 5a | x |^{2} + 8a | x | - 4a & 1 < | x | < 2 \\ 0 & others \end{array} \right. $
其中 a 通常取值为 -0.5,代入之后得
$ W(x) = \left\{ \begin{array}{cc} 1.5 | x |^{3} - 2.5 | x |^{2} + 1 & | x | \le 1 \\ -0.5 | x |^{3} + 2.5 | x |^{2} - 4 | x | + 2 & 1 < | x | < 2 \\ 0 & others \end{array} \right. $
双三次插值的权重值是分水平和垂直两个方向分别求得的,计算公式是一样的,都是上面的公式。对于周围 16 个点中的每一个点,其坐标值为(x, y),而目标图像中的目标像素在原图像中的映射坐标为 p(u, v)。那么通过上面的公式可以求得其水平权重 W(u - x),垂直权重 W(v - y)。将 W(u - x) 乘以 W(v - y) 得到最终权重值,然后再用最终权重值乘以该点的像素值,并对 16 个点分别做同样的操作并求和,就得到待插值的像素值了。公式如下
$ p(u, v) = \sum^{3}_ {x = 0} \sum^{3}_ {y=0} W(u - x) * W(v - y) * p(x, y) $
其中 p() 表示该像素的像素值
编码原理:视频究竟是怎么编码压缩的
对每一帧图像,划分成一个个块来进行编码,这在 H264 中叫做宏块,而在 VP9、AV1 中称之为超级块。宏块大小一般是 16x16(H264、VP8),32x32(H265、VP9),64x64(H265、VP9、AV1),128x128(AV1)这几种
图像一般都是有数据冗余的,主要包括以下 4 种:
- 空间冗余 比如将一帧图像划分成一个个 16x16 的块之后,相邻的块很多时候都有比较明显的相似性,这种就叫空间冗余
- 时间冗余 一个帧率为 25fps 的视频中前后两帧图像相差只有 40ms,两张图像的变化是比较小的,相似性很高,这种叫做时间冗余
- 视觉冗余 人眼对图像中高频信息敏感度小于低频信息,有时候去除图像中的一些高频信息,人眼看上去跟不去除高频信息差别不大
- 信息熵冗余 我们一般会使用 zip 等压缩工具去压缩文件,这对图像也可以做
对于一个 YUV 图像,我们把它划分为一个个 16x16 的宏块(以 H264 为例),Y、U、V 分量的大小分别是 16x16、8x8、8x8。这里我们只对 Y 分量进行分析(U、V 分量同理)。假设 Y 分量这 16x16 个像素就是一个个数字,我们从左上角开始之字形扫描每一个像素值,则可以得到一个“像素串”。如下图所示
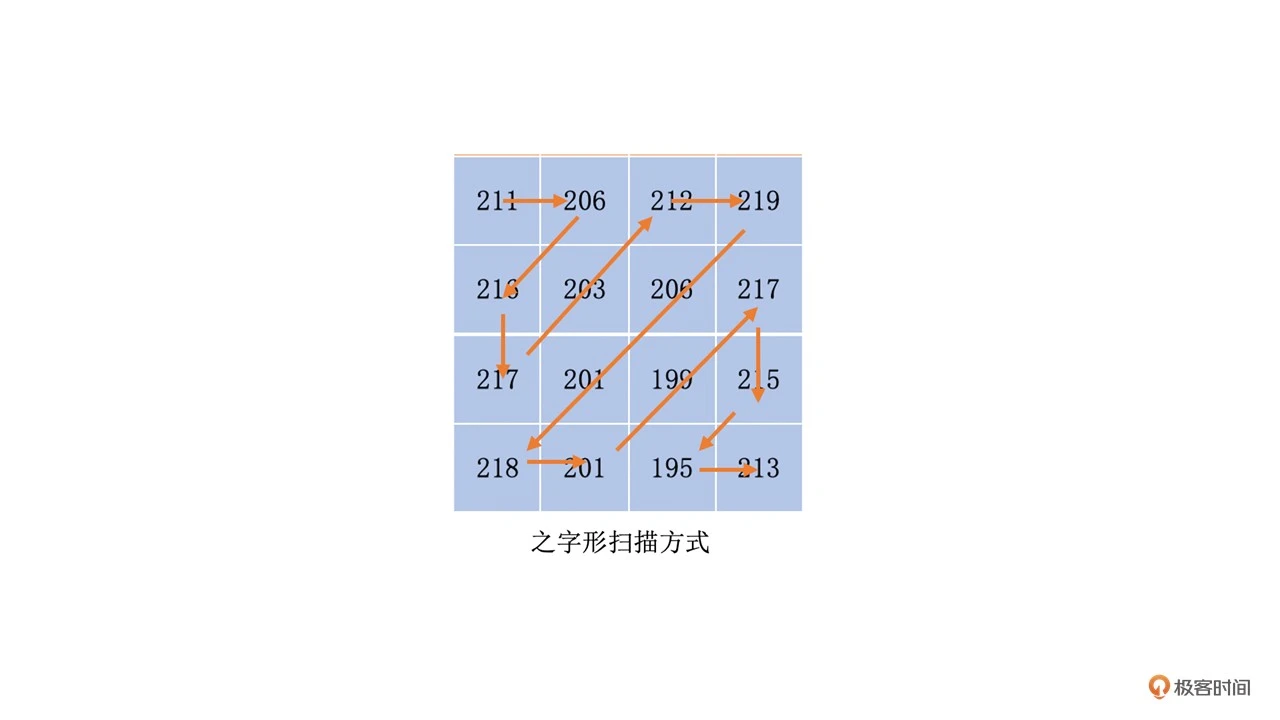
比如将 “aaaabbbccccc” 压缩成 “4a3b5c”,这叫做行程编码。我们必须要使得编码前的字符串中出现比较多连续相同的字符。最好是一连串数字很小(比如 0)的“像素串”,因为 0 在二进制中只占 1 个位就可以了
首先第一步,我们通过减少图像块的空间冗余和时间冗余来接近这个目标。我们可以在编码时进行帧内预测和帧间预测
帧内预测就是在当前编码图像内部已经编码完成的块中找到与将要编码的块相邻的块。一般就是即将编码块的左边块、上边块、左上角块和右上角块,通过将这些块与编码块相邻的像素经过多种不同的算法得到多个不同的预测块
然后我们再用编码块减去每一个预测块得到一个个残差块。最后,我们取这些算法得到的残差块中像素的绝对值加起来最小的块为预测块。而得到这个预测块的算法为帧内预测模式
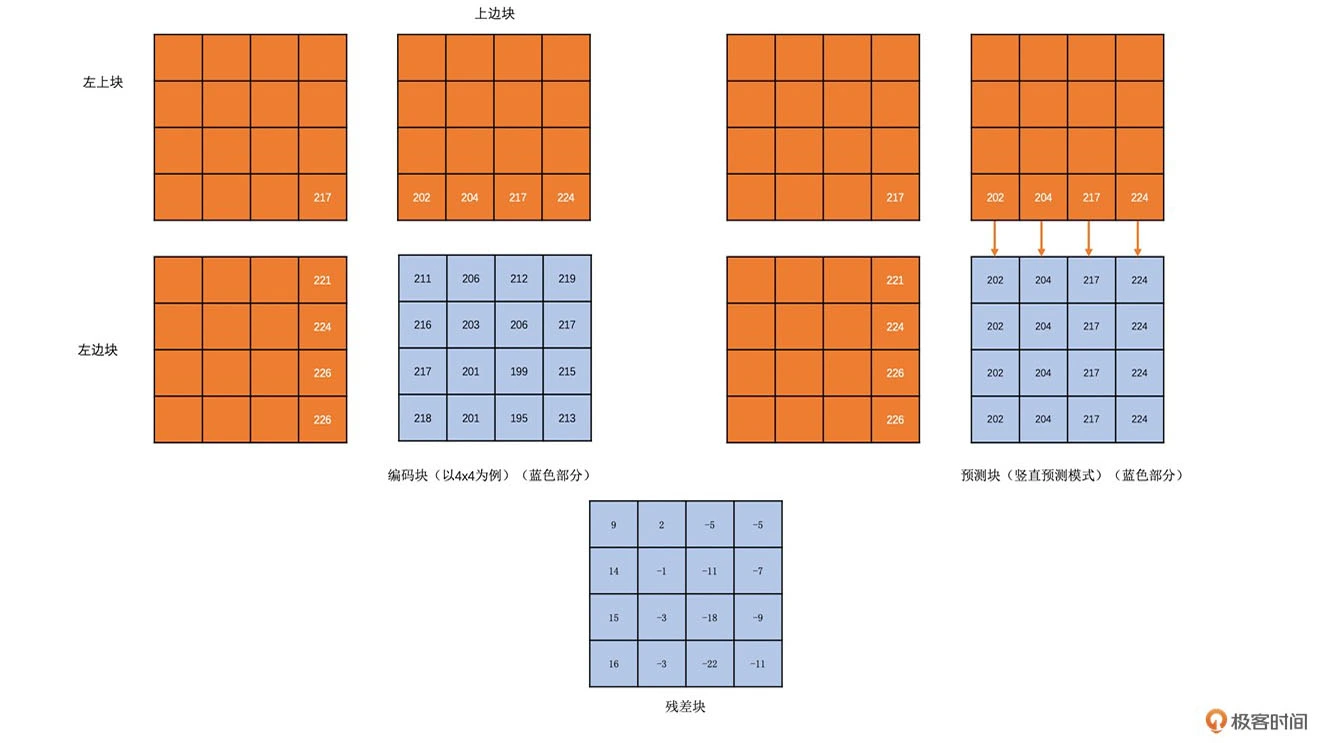
由于这个残差块中像素的绝对值之和最小,这个残差块的像素值经过扫描之后的“像素串”是不是就比直接扫描编码块的“像素串”中的像素值更接近 0 了?
帧间预测也一样。对已经编码完的图像,循环遍历每一个块,将它作为预测块,用当前的编码块与这个块做差值,得到残差块,取残差块中像素值的绝对值加起来最小的块为预测块,预测块所在的已经编码的图像称为参考帧。预测块在参考帧中的坐标值(x0, y0)与编码块在编码帧中的坐标值(x1, y1)的差值(x0 - x1, y0 - y1)称之为运动矢量。而在参考帧中去寻找预测块的过程称之为运动搜索。事实上编码过程中真正的运动搜索不是一个个块遍历寻找,而是有快速的运动搜索算法
为了分离图像块的高频和低频信息,我们需要将图像块变换到频域。常用的变换是 DCT 变换。DCT 变换又叫离散余弦变换。在 H264 里面,如果一个块大小是 16x16 的,我们一般会划分成 16 个 4x4 的块(当然也有划分成 8x8 做变换的)。然后我们对每个 4x4 的块做 DCT 变换得到相应的 4x4 的变换块
变换块的每一个“像素值”我们称为系数。变换块左上角的系数值就是图像的低频信息,其余的就是图像的高频信息,并且高频信息占大部分。低频信息表示的是一张图的总体样貌。一般低频系数的值也比较大。而高频信息主要表示的是图像中人物或物体的轮廓边缘等变化剧烈的地方。高频系数的数量多,但高频系数的值一般比较小(注意不是所有的高频系数都一定小于低频,只是大多数高频系数比较小)。如下图所示(黄色为低频,绿色为高频):
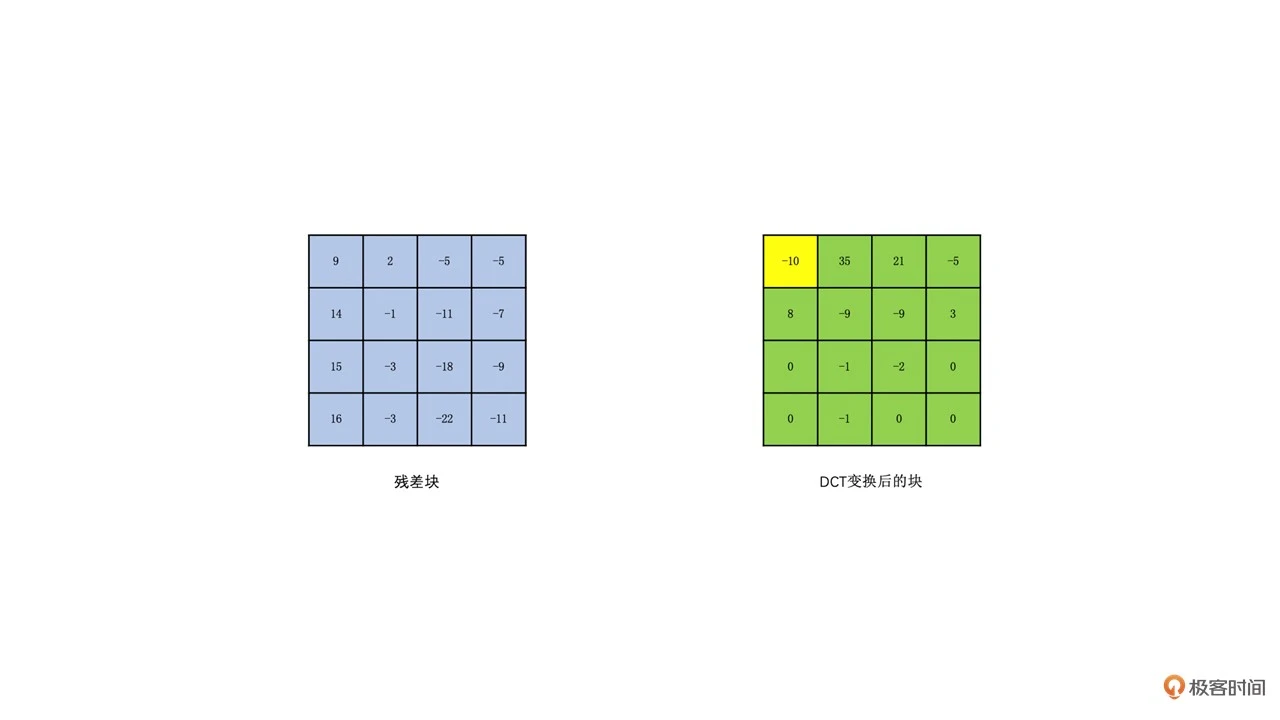
我们让变换块的系数同时除以一个值,这个值我们称之为量化步长,也就是 QStep(QStep 是编码器内部的概念,用户一般使用量化参数 QP 这个值,QP 和 QStep 一一对应,你可以自行去网上查询一下转换表),得到的结果就是量化后的系数。QStep 越大,得到量化后的系数就会越小。同时,相同的 QStep 值,高频系数值相比低频系数值更小,量化后就更容易变成 0。这样一来,我们就可以将大部分高频系数变成 0。如下图所示
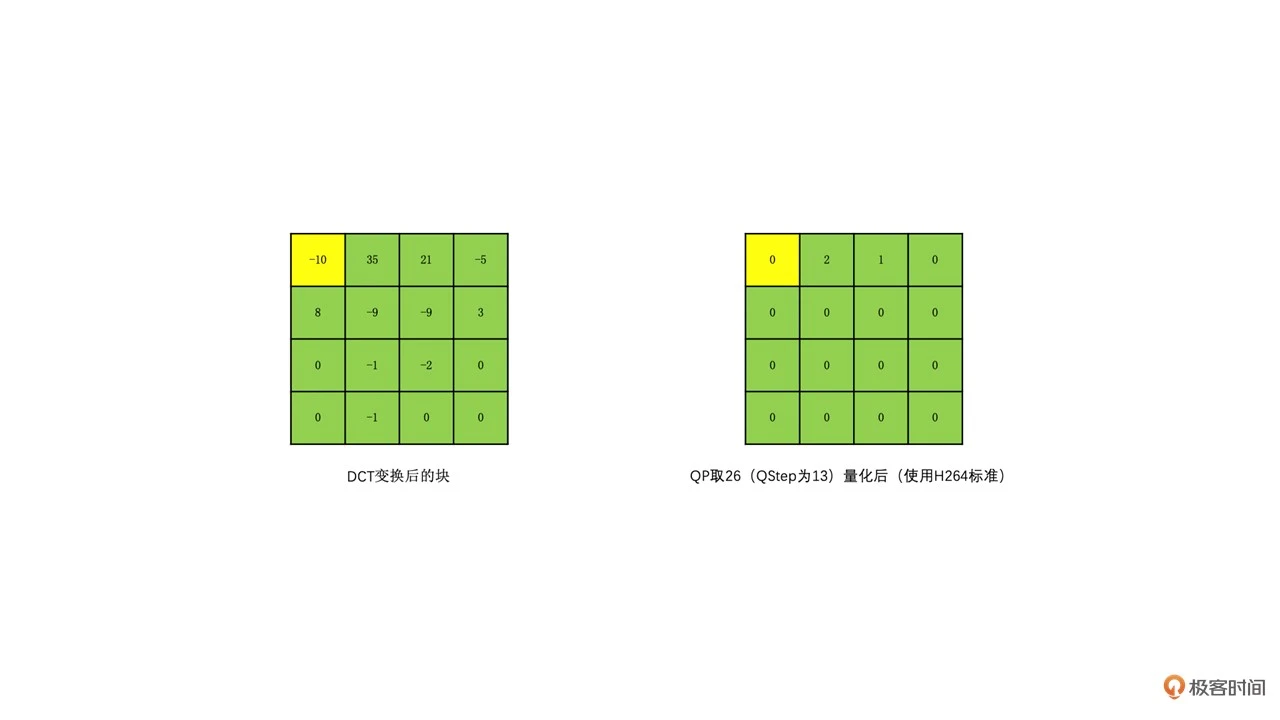
解码的时候,我们会将 QStep 乘以量化后的系数得到变换系数,很明显这个变换系数和原始没有量化的变换系数是不一样的,这个就是我们常说的有损编码
损失由 QStep 来控制,QStep 越大,损失就越大。QStep 跟 QP 一一对应,也就是说确定了一个 QP 值,就确定了一个 QStep。所以从编码器应用角度来看,QP 值越大,损失就越大,从而画面的清晰度就会降低
编码器的对比及选择
H264 和 H265 是需要专利费的,而 VP8 和 VP9 完全免费。由于 H265 需要付高额的版权费,以谷歌为首的互联网和芯片巨头公司组织了 AOM 联盟,并开发了新一代压缩编码算法 AV1,并宣布完全免费
WebRTC 默认使用 VP8
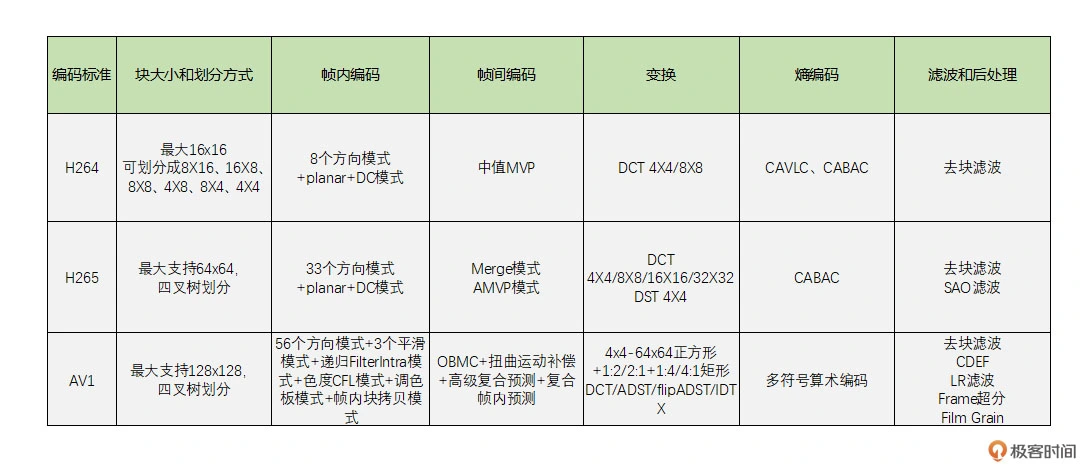
从上面表格中可以看到,标准越新,最大编码块就越大,块划分的方式也越多,编码模式也就越多。因此压缩效率也会越高,但是带来的编码耗时也越大。所以在选择编码器的时候需要根据实际应用场景来选择,同时考虑专利费问题,考虑有没有硬件支持,目前 H264 和 H265 的硬件支持已经很好了,AV1 才刚开始,硬件支持较少,之后会有更多硬编硬件支持
我做了个简单的编码清晰度和耗时对比,都是在软件编码下进行的。具体如下表。我们可以看到相同码率下,AV1 清晰度稍好于 H265,而 H264 最差,但是编码耗时则相反,AV1 最高,H265 次之,H264 速度最快
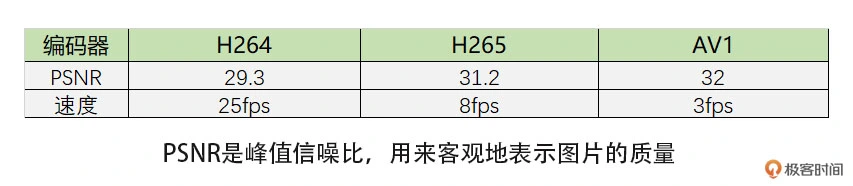
所以,如果是在性能比较差的机器上编码,最好使用 H264 和 VP8,如果机器比较新,可以考虑 H265。中等机器如果支持 H265 硬编也可以考虑。但 H265 需要考虑专利费的问题。同时浏览器原生不支持 H265 编码,所以有这方面需求可以考虑使用 VP9,甚至可以考虑 AV1。另外,由于 AV1 原生标准就支持屏幕编码的优化,所以屏幕编码场景下可以考虑使用 AV1
Tips
早期反射
https://ccrma.stanford.edu/~jos/pasp/Early_Reflections.html
混响环境的脉冲反应的早期反射部分经常是头 100ms。然而,为更好的精确度,应该扩展到混响达到它的渐进统计行为的时间
因为早期反响相对稀疏且持续一个相对短的时间,它们经常用拍打延迟线 (TDL) 实现
如果算力可负担,最好空间化早期反射以便它们从 3D 空间的正确方向过来。早期反射在空间印象上有很强的影响,例如,听者探知听力空间形状
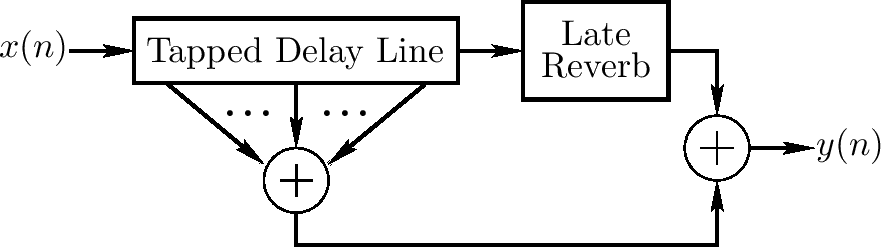
上图显示一个早期和后续混响独立实现的一个混响基本示意图。TDL 上的拍打可能包括空气吸收模拟的低通过滤
当后续混响逻辑上在早期反射结束后开始,如上图,他可能实际上更有成本效益地从 TDL 一个早期拍打(或一系列拍打)反馈后续混响单位,这样覆盖部分。这对后续混响需要时间来构建完全密度时有帮助
通常早期反射可用于后续混响模拟。例如,通常长延迟线的输入信号可在各点总结,因此实现一个转置的拍打延迟线
可观察到好的音乐大厅有立体声记录的脉冲反应以一个大约延迟 1.9 秒的平滑的衰减快速边沿化
Share
什么是拷贝交换语义?
https://stackoverflow.com/questions/3279543/what-is-the-copy-and-swap-idiom/3279550#3279550
概述
为什么我们需要拷贝交换语义?
任何管理一个资源的类需要实现 Big Three Rule
The rule of three 如果你需要直接定义析构、拷贝构造或拷贝赋值操作,你需要直接定义所有这三个
当复制构造和析构的目的和实现是直接的,拷贝赋值函数是最微妙且困难的。它如何做?需要避免什么缺陷?
拷贝交换语义是一个解决方案,且协助赋值操作达成两个事情:避免代码重复,避免强异常保证
它如何实施?
概念上,它通过使用拷贝构造函数功能来创建一个数据的本地拷贝,然后用 swap 函数获取拷贝的数据,并用它与旧数据交换。临时拷贝然后被析构
为了使用拷贝交换语义,我们需要三件事情:一个拷贝构造函数,一个析构和一个交换函数
一个交换函数是一个不抛异常的函数交换一个类的两个对象,成员到成员。我们可尝试使用 std::swap,但这是不行的;std::swap 使用拷贝构造和拷贝赋值函数,且我们最终尝试定义赋值函数
一个深度的解释
目标
让我们考虑一个具体的例子。我们想要管理一个动态数组。我们开始一个构造函数、拷贝构造函数和析构函数
#include <algorithm>
#include <cstddef>
class dumb_array {
public:
dumb_array(std::size_t size = 0) : mSize(size),
mArray(mSize ? new int[mSize]() : nullptr) {}
dumb_array(const dumb_array& other) : mSize(other.mSize),
mArray(mSize ? new int[mSize] : nullptr) {
std::copy(other.mArray, other.mArray + mSize, mArray);
}
~dumb_array() {
delete [] mArray;
}
private:
std::size_t mSize;
int* mArray;
};
这个类可以很好地管理数组,但它需要 operator= 来协助
一个失败的解决方案
这里有一个实现
dumb_array& operator=(const dumb_array& other) {
if (this != other) {
delete [] mArray;
mArray = nullptr;
mSize = other.mSize;
mArray = mSize ? new int[mSize] : nullptr;
std::copy(other.mArray, other.mArray + mSize, mArray);
}
return *this;
}
然而,这个实现有三个问题:
-
首先是自我赋值测试
通常情况下自我赋值很少发生,所以大多数情况下该检测是一个浪费
-
只提供基本异常保障。如果 new int[mSize] 失败,*this 已被修改,为保证强异常,代码应该如下
dumb_array& operator=(const dumb_array& other) { if (this != other) { std::size_t newSize = other.mSize; int* newArray = mSize ? new int[mSize] : nullptr; std::copy(other.mArray, other.mArray + mSize, newArray); delete [] mArray; mSize = other.mSize; mArray = newArray; } return *this; } -
代码重复
一个成功的解决方案
拷贝交换语义将解决这些问题。我们需要添加一个 swap 函数
class dumb_array {
public:
// ...
friend void swap(dumb_array& first, dumb_array& second) {
using std::swap;
swap(first.mSize, second.mSize);
swap(first.mArray, second.mArray);
}
// ...
};
我们的赋值函数
dumb_array& opeartor=(dumb_array other) {
swap(*this, other);
return *this;
}
C++11?
管理资源我们现在是 The Rule of Four,移动构造函数如下:
class dumb_array {
public:
// ...
dumb_array(dumb_array&& other) noexcept
: dumb_array() {
swap(*this, other);
}
// ...
};