Table of Contents

许多组合统计问题带一个有参数n的$ a_ {n} $的解决方案，可被解决为找到一个 $ a_ {n} $的递归关系且然后解决该递归。有时候这通过引入一个普通生成函数

$ f(x) := \sum_ {n \ge 0}a_ {n}x^{n} $

或一个指数生成函数

$ f(x) := \sum_ {n \ge 0}a _{n} \frac{x^{n}}{n!} $

且使用递归来找到一个等式或一个f(x)的导函数，且解决该等式。我们将展示一些技巧

例子 14.1 作为一个介绍，考虑例子10.1。设 $ \pi $为一个derangement $ \{1,2,\ldots,n+1\} $。对 $ \pi(n + 1) $有n个选择。如果 $ \pi(n + 1) = i $且 $ \pi(i) = n + 1 $ 则 $ \pi $也是也是集合 $ \{1,2,\ldots, n\} \backslash \{i\} $的一个dearrangement。如果 $ \pi(n + 1) = i $且 $ \pi(i) \ne n + 1 = \pi(j) $，则用i位的替代 $ \pi(j) $得到一个集合 $ \{1,2,\ldots,n\} $的dearrangement。因此

$ d_ {n+1} = n(d_ {n} + d_ {n-1}) $

这也是10.3的一个结果。设D(x)为序列 $ d_ {0} = 1, d_ {1} = 0, d_ {2}, \ldots $的指数生成函数，我们可发现

$ (1 - x) D^{\prime}(x) = x D(x) $

且从这我们发现 $ D(x) = e^{-x} / (1 - x) $且(10.2)

在许多情况下，我们使用生成函数只作为订阅设备，且我们的加法、乘法操作（甚至替换和求导）会做形式化地解释。它可能给出一个形式化指数系列（代数对象）的完整严谨的理论和我们在附录2中给出一个这个理论的一个简介。在多数情况下，容易验证这些操作是合理的。如果我们使用的系列是收敛的，则我们可使用所有分析中适合的知识来考虑这些系列

例子 14.2 假设我们有k个盒子标号从1到k且假设盒子i有 $ r_ {i} $个球，$ 1 \le i \le k $。一个形式化的订购设备列出所有可能的配置让对应 $ x^{r_ {1}}_ {1}x^{r_ {2}}_ {2} \cdots x^{r_ {k}}_ {k} $在乘积中

$ (1 + x_ {1} + x^{2}_ {1} + \cdots)(1 + x_ {2} + x^{2}_ {2} + \cdots) \cdots (1 + x_ {k} + x^{2}_ {k} + \cdots) $

我们可收集所有的项目包含n个球通过设 $ x_ {i} = x $，对所有的i，且考虑等于 $ x^{n} $的项。因此我们发现分n个球到k个不同的盒子的方法数是 $ (1 - x)^{-k} $展开后 $ x^{n} $的系数，且通过10.6我们得到它为 $ {k-1+n \choose n} $，这给出了定理13.1的另一个证明

在许多情况下，我们感兴趣的组合问题导致一个常系数的线性迭代关系，容易通过标准方法解决

例子 14.3 我们考虑长度为n的路径在X-Y平面中，开始于(0, 0)和步骤R：$ (x, y) \to (x + 1, y), L: (x, y) \to (x - 1, y) $和 $ U: (x, y) \to (x, y + 1) $。我们需要一个步骤R不跟着步骤L之后且相反。设 $ a_ {n} $记为这样的路径的数目。首先观察如果我们记 $ b_ {n} $为开始于步骤U的长度为n的路径数，则 $ b_ {n} = a_ {n-1} $且进一步地有 $ b_ {n+m} \ge b_ {n}b_ {m} $且 $ b_ {n} \le 3^{n-1} $。这样通过Fekete引理，引理11.6，$ \lim_ {n \to \infty} b^{1 / n}_ {n} $存在且最多为3。接着，注意 $ a_ {0} = 1 $且 $ a_ {1} = 3 $。我们分割长度为n的路径的集合为依赖最后的一步或两步的子集。明显地有 $ a_ {n-1} $个路径以步骤U结尾。取长度为n - 1的路径且重复最后的步骤如果它是L或R，且如果最后一步是U则接一个步骤L。在这样的方法上我们获得长度为n的所有路径以LL, RR或UL结尾。这样有 $ a_ {n-1} $个。仍然统计以UR结尾且这样的有 $ a_ {n-2} $个。我们显示

$ a_ {n} = 2a_ {n-1} + a_ {n-2} $

设 $ f(x) = \sum^{\infty} _{n=0} a _ {n} x^{n} $。则递归意味着

$ f(x) = 1 + 3x + 2x(f(x) - 1) + x^{2}f(x) $

例如：

$ f(x) = \frac{1+x}{1 - 2x - x^{2}} = \frac{\frac{1}{2} \alpha}{1 - \alpha x} + \frac{\frac{1}{2} \beta}{1 - \beta x} $

$ \alpha = 1 + \sqrt{2}, \beta = 1 - \sqrt{2} $。因此

$ a_ {n} = \frac{1}{2} (\alpha^{n+1} + \beta^{n+1}) $

且我们发现 $ \lim_ {n \to \infty} a^{1 / n}_ {n} = 1 + \sqrt{2} $

例子 14.4 设a(r, n)，$ 0 \le r \le n $，记为例子13.1（a(0, 0) = 1）的问题的解决方案数。我们分割可能的序列集合为两个子集：$ x_ {1} = 1 $和 $ x_ {1} > 1 $。头一个子集明显包含a(r - 1, n - 2)个元素，第二个子集有a(r, n - 1)个元素。这样

a(r, n) = a(r, n - 1) + a(r - 1, n - 2) (n > 1)

从这个递归，我们可归纳证明结果$ a(r, n) = {n - r + 1 \choose r} $。使用生成函数更困难一些。尝试

$ f(x, y) := \sum^{\infty}_ {n = 0} \sum^{\infty}_ {r = 0} a(r, n)x^{n}y^{r} $

从（14.2）我们发现

$ f(x, y) = 1 + x + xy + x(-1 + f(x, y)) + x^{2}yf(x, y) $

则

$ f(x, y) = \frac{1 + xy}{1 - x - x^{2}y} = \frac{1}{1 - x} + \sum^{\infty}_ {a = 1} \frac{x^{2a - 1}y^{a}}{(1 - x)^{a+1}} $

对 $ (1 - x)^{-a - 1} $用(10.6)替换产生需要的给a(r, n)的二项式系数

如我们在例子14.3中所见（和问题14A）一个带线性递归导致一个有理函数为生成函数（反之也然）。如果 $ a_ {n} = \sum^{l}_ {k=1}a_ {k}a_ {n-k} \qquad (n > 1) $和 $ f(x) = \sum^{\infty}_ {n=0} a_ {n}x^{n} $，则 $ (1 - \sum^{l}_ {k=1} \alpha_ {k}x^{k})f(x) $是一个指数系列，如果n > 1则其是 $ x^{n} $的系数

如下的例子由Klarner显示一个线性递归的有趣例子其通过生产函数的帮助找到且其在组合中不是都很明显

例子 14.5 考虑平面的配置，称为polyominoes，如下图。配置包含层，每层包含连续的方块。两个连续层在方块的边( $ \ge 1 $)相遇（更精确地说，我们考虑水平凸polyominoes）

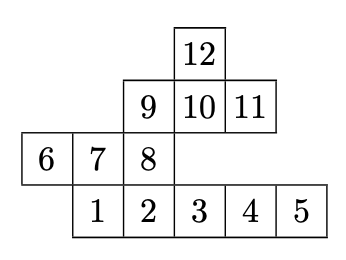
设 $ a_ {n} $记为n方块的polyominoes数且定义 $ f(x) := \sum^{\infty}_ {n=1} a_ {n}x^{n} $。为找到f，我们对polyominoes数引入a(m, n)，其底层有m个方块（总共是n个）。我们定义a(m, n) := 0如果m > n。明显地

$ a(m, n) = \sum^{\infty}_ {l = 1} (m + l - 1)a(l, n - m) $

我们定义

$ F(x, y) := \sum^{\infty}_ {n=1} \sum^{\infty}_ {m=1} a(m, n) x^{n} y^{m} $

则f(x) = F(x, 1)。因为系列我们定义

$ g(x) := \sum^{\infty}_ {n=1} \sum^{\infty}_ {m=1} ma(m, n)x^{n} $

我们想要写为

$ g(x) = \left( \frac{\partial F}{\partial y} \right)_ {y=1} $

甚至我们有一个形式化指数系列的理论，它可显示F(x, y)的右边收敛到一个有效的大范围。这给我们机会来显示一个快速的方法获得一个对 $ a_ {n} $粗略的估计。标号上图中polyomino的方块数。对每个方块相关联一个0、1的四元组 $ (x_ {0}, x_ {1}, x_ {2}, x_ {3}) $，$ x_ {0} = 1 $意味着有一个polyomino的方块在本方块之下，$ x_ {1} = 1 $意味着有一个polyomino的方块在本方块左边，$ x_ {2} = 1 $意味着有一个polyomino的方块在本方块上面，$ x_ {3} = 1 $意味着有一个polyomino的方块在本方块右边。例如，在上图中，第一个四元组是(0, 0, 1, 1)。四元组序列唯一确定polyomino。这显示 $ a_ {n} \le 15^{n} $。根据这个和(14.3)我们发现 $ a(m, n) \le n \cdot 15^{n-m} $，这足以得出上式。有

$ F(x, y) = \frac{xy}{1 - xy} + \frac{(xy)^{2}}{(1 - xy)^{2}} f(x) + \frac{xy}{1 - xy} g(x) $

两边求导并让y = 1，我们发现

$ f(x) = \frac{x(1 - x)^{3}}{1 - 5x + 7x^{2} - 4x^{3}} $

从上式我们看到 $ a_ {n} $满足递归关系

$ a_ {n} = 5a_ {n-1} - 7a_ {n-2} + 4a_ {n-3} \qquad (n \ge 5) $