Table of Contents
Colorings of graphs and Ramsey’s theorem
定理 如果 $ K_ {n} $的边着上红色或蓝色,且 $ r_ {i}, i = 1, 2, \ldots, n $,记为顶点i作为端点的红边个数。且如果 $ \Delta $记为单色三角形的个数,则
$ \Delta = {n \choose 3} - \frac{1}{2} \sum^{n}_ {i=1} r_ {i}(n - 1 - r_ {i}) $
证明:$ K_ {n} $中每个三角形不是单色的话有两个顶点是红边和蓝边的交点。在第i个顶点上,两个这样的边可被选择有 $ r_ {i} (n - 1 - r_ {i}) $个,进而得证
定理 设 $ r \ge 1 $且 $ q_ {i} \ge r, i = 1, 2, \ldots, s $。存在一个最小的正整数 $ N(q_ {1}, q_ {2}, \ldots, q_ {s}; r) $有如下属性。设S为有n个元素的集合。假设所有 $ {n \choose r} $ S的r子集被分割成一个互斥家族 $ T_ {1}, \ldots, T_ {s} $(颜色)。则如果 $ n \ge N(q_ {1}, q_ {2}, \ldots, q_ {s}; r) $有一个i,$ 1 \le i \le s $,且一些 $ q_ {i} $S的子集,其每个r子集在 $ T_ {i} $中
证明:我们只给出s = 2时的证明。一般化情况只多了些记账步骤
(a) 定理对r = 1且N(p,q;1) = p + q - 1来说是真的
(b) 对任意r和 $ p \ge r $,明显地N(p,r;r) = p且相似地N(r,q;r) = q, $ q \ge r $
(c) 我们使用归纳法。假设定理对r - 1时是真的。我们现在看p + q,使用(b)。这样我们可定义 $ p_ {1} = N(p - 1, q; r), q_ {1} = N(p, q - 1; r) $。设S为有n个元素的集合,$ n \ge 1 + N(p_ {1}, q_ {1}; r - 1) $。设S的r子集用两种颜色着色,分别为红色和蓝色。在 $ K_ {6} $的证明中,我们任意选S中的一个元素a。我们现在定义一个$ S^{\prime} $的着色(r - 1)子集,$ S^{\prime} := S \ \{a \} $,给定 $ X \subseteq S^{\prime} $跟 $ X \cup \{a\} $有相同的颜色。通过归纳 $ S^{\prime} $要么包含一个大小为 $ p_ {1} $的子集A使得所有它的(r - 1)子集为红色或一个大小为 $ q_ {1} $的子集B使得所有它的(r - 1)子集为蓝色。不失一般性这里我们说第一种情况发生。因为A有 $ N(p - 1, q; r) $个元素,存在两种可能。第一是A有一个q元素的子集其所有r子集为蓝色。另一种是A有一个p - 1元素的子集 $ A^{\prime} $其所有r-子集为红色。集合 $ A^{\prime} \cup \{a \} $也有这个属性因为 $ A^{\prime} \subseteq A $。这证明了定理且进一步我们显示
$ N(p,q;r) \le N(N(p-1,q;r), N(p, q-1;r);r-1) + 1 $
上式的一个特殊情况发生在当我们回到两个颜色的一个图形着色(r = 2)时。使用(a)我们发现
$ N(p,q;2) \le N(p-1,q;2) + N(p,q-1;2) $
问题 显示上式等号成立的话右边的两项不能都是偶数
定理 $ N(p, q; 2) \le {p + q - 2 \choose p - 1} $
证明:因为N(p,2;2) = p,根据二项式系数我们得到该式子成立
通过之前的式子,我们有 $ N(3,4;2) \le 9 $。为显示等式成立,我们有颜色 $ K_ {8} $使得没有红色三角和蓝色 $ K_ {4} $。我们这么做:编号顶点为 $ \mathbb{Z}_ {8} $的元素。让边 $ \{i, j\} $为红色当且仅当 $ i - j \equiv \pm 3 $ 或 $ i - j \equiv 4 \; (mod \; 8) $
问题 使用相同的方法显示N(4,4;2) = 18且N(3,5;2) = 14
有更多的工作显示N(3,6;2) = 18, N(3,7;2) = 23, N(3,8;2) = 28, N(3,9;2) = 36,没有其他的N(p,q;2)值已知
这个领域一个有趣的问题之一已经30年没有进展,即N(p,p;2)的渐近属性。我们通过之前的定理知道
$ N(p,p;2) \le {2p-2 \choose p-1} \le 2^{2p-2} $
我们现在显示N(p,p;2)是指数级增长,使用一个经常在组合数学中用到的方法。它通常认为是概率的因为它估计一个单色 $ K_ {p} $的随机着色的概率。考虑一个 $ K_ {n} $。有 $ 2^{ {n \choose 2} } $种用红蓝着色边的方法。现在固定一个子图 $ K_ {p} $。有 $ 2^{ {n \choose 2} - {p \choose 2} + 1} $种让 $ K_ {p} $为单色。$ K_ {p} $是单色的着色数最多为 $ {n \choose p} $(因为我们可能统计某种颜色多次)。如果这个数小于着色总数,则存在没有 $ K_ {p} $的着色。使用 $ {n \choose p} < n^{p} / p! $,我们发现这样的着色存在如果$ n < 2^{p / 2} $(除非p = 2)。这证明了如下定理
定理 $ N(p,p;2) \ge 2^{p/2} $
定理 设G为事件 $ A_ {1}, \ldots, A_ {n} $的依赖图。假设 $ Pr[A_ {i}] \le p, i = 1, \ldots, n $且G中每个顶点有度数 $ \le d $。如果4dp < 1,则 $ \cap \bar{A_ {i}} \ne \emptyset $
证明:我们首先显示对索引集合 $ \{ i_ {i}, i_ {2}, \ldots, i_ {m} \} $的每个子集
$ Pr[A_ {i_ {1}} | \bar{A_ {i_ {2}}} \ldots \bar{A_ {i_ {m}}}] \le \frac{1}{2d} $
当m=1时是平凡的且对m=2我们有
$ Pr[A_ {1} | \bar{A_ {2}}] \le \frac{p_ {1}}{1 - p_ {2}} \le \frac{1}{4d - 1} < \frac{1}{2d} $
为方便起见,我们让 $ i_ {j} = j $且 $ p_ {i} := Pr[A_ {i}] $
假设在G中,1邻接 $ 2, 3, \ldots, q $且不邻接 $ q + 1, \ldots, m $。我们有
$ Pr[A_ {1} | \bar{A_ {2}} \ldots \bar{A_ {m}}] = \frac{Pr[A_ {1}\bar{A_ {2}} \ldots \bar{A_ {q}} | \bar{A_ {q+1}} \ldots \bar{A_ {m}}]}{Pr[\bar{A_ {2}} \ldots \bar{A_ {q}} | \bar{A_ {q+1}} \ldots \bar{A_ {m}}]} $
其分子最多为
$ Pr[A_ {1} | \bar{A_ {q+1}} \ldots \bar{A_ {m}}] = Pr[A_ {1}] \le \frac{1}{4d} $
使用归纳假设,我们发现分子至少
$ 1 - \sum^{q}_ {i=2}Pr[A_ {1}| \bar{A_ {q+1}} \ldots \bar{A_ {m}}] \ge 1 - \frac{q-1}{2d} \ge \frac{1}{2} $
这证明了定理。我们现在有
$ Pr[\bar{A_ {1}} \ldots \bar{A_ {n}}] = \prod^{n}_ {i=1}Pr[\bar{A_ {i}} | \bar{A_ {1}} \ldots \bar{A_ {i-1}}] \ge (1 - \frac{1}{2d})^{n} > 0 $
定理 $ N(p,p;2) \ge c \cdot p \cdot 2^{p / 2} $,c是常量
证明:考虑 $ K_ {n} $和用两种颜色对边随机着色。对每个k个顶点的集合S设 $ A_ {S} $为在S上为单色的事件。我们希望断言在随机着色时,至少有一个不含k顶点单色子图。我们定义依赖图,其使S和T邻接当且仅当 $ | S \cap T | \ge 2 $。例如,S和T的子图有公共边。G的度数最多 $ {k \choose 2} {n \choose k-2} $。事件 $ A_ {S} $都有概率 $ 2^{1 - {k \choose 2} } $。利用之前的定理和Stirlinng公式和一些小计算,我们能得到结果
我们已经给出Ramsey定理在组合领域的一些例子。我们将提及另一个例子,由B. L. var der Waerden命名。它描述存在一个数N(r)使得如果 $ N \ge N(r) $且从1到N的数着色为红色或蓝色,则集合中有一个长度为r的单色
定理 对一个给定的n,有一个整数N(n)使得对任意平面上点 $ N \ge N(n) $的收集,没有3个点在一条线上,有一个n个点的子集形成一个凸n边形
证明:(i) 首先我们观察如果我们有n个点,没有3个点在一条线上,则它们形成一个n凸边形当且仅当每4个点形成的4边形是凸的
(ii) 我们现在声称 N(n) = N(n,n;3)。设S为N(n)个点的集合。对点着色为红色三角和蓝色三角,如果路径从最小点到中点到最大点是顺时针的,反之是逆时针的。有一个n个顶点的子集其所有三角为相同颜色,如红色。我们将显示该集合不包含下图的配置
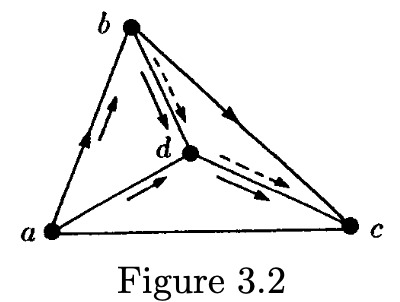
不失一般性我们有a < b < c。从三角形adc,我们看到a < d < c。则从三角形abd有a < b < d。但三角形bcd是蓝色的,矛盾。这样所有n点集合的4边形是凸的