Table of Contents
古代的求积法
特殊的曲面曲线的求积法自古就为人所知。阿基米德以计算球面及体积闻名,阿基米德还设计了如下的方法,用一根弦限制的抛物线碎片很好地计算出了面积
AB是抛物线的弦,OM是通过它中点的直径,那么抛物线和弦所围成的面积S是三角形OAB面积T的 $ \frac{4}{3} $,即
$ S = \frac{4}{3} T $
用现代的坐标法,OM为x轴,O处的切线为y轴,抛物线的方程式为 $ y^{2} = cx $,OM = a,AB的极点N为(-a, 0),即O为NM的中点,弦AB与两端的切线形成的三角形NAB的面积是OAB的两倍
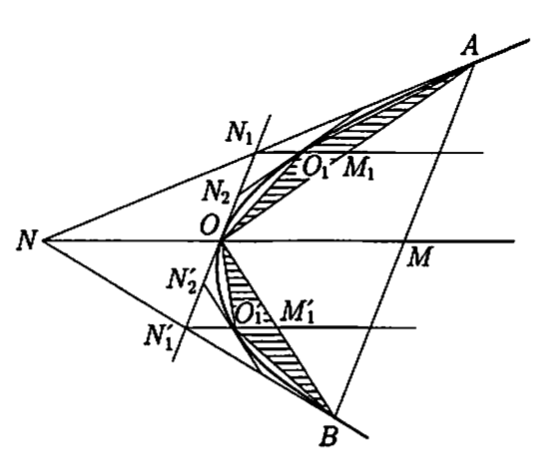
同样的关系对弦OA、OB也成立,上图 $ O_ {1}M_ {1} = \frac{1}{2} N_ {1}M_ {1} = \frac{1}{4} OM $。则 $ \bigtriangleup O O^{\prime}_ {1}B = \frac{1}{4} \bigtriangleup OBM $。现在 $ \bigtriangleup OO_ {1}A, \bigtriangleup OO^{\prime}_ {1}B $的面积的和为 $ T_ {1} $
$ T_ {1} = \frac{1}{4} T $
同样的弦 $ O_ {1}A, OO_ {1}, OO^{\prime}_ {1}, O^{\prime}_ {1}B $为底做同样的三角形,这样的面积的和 $ T_ {2} $
$ T_ {2} = \frac{1}{4} T_ {1} = \frac{1}{4^{2}} T $
继续这样的操作,可做出 $ T, T_ {1}, T_ {2}, \ldots $,这样的面积统计得
$ S = T + \frac{T}{4} + \frac{T}{4^{2}} + \cdots = T(1 + \frac{1}{4} + \frac{1}{4^{2}} + \cdots) = \frac{4}{3} T $
由于
$ T + T_ {1} + \cdots + T_ {n-1} + T_ {n} < S < T + T_ {1} + \cdots + T_ {n-1} + 2T_ {n} $
$ T(1 + \frac{1}{4} + \cdots + \frac{1}{4^{n}}) < S < T(1 + \frac{1}{4} + \cdots + \frac{1}{4^{n}} + \frac{1}{4^{n}}) $
$ \frac{4}{3}T(1 - \frac{1}{4^{n+1}}) < S < \frac{4}{3}T(1 - \frac{1}{4^{n+1}}) + \frac{T}{4^{n}} $
$ -\frac{1}{3} \cdot \frac{T}{4^{n}} < S - \frac{4}{3} T < \frac{2}{3} \cdot \frac{T}{4^{n}} $
由于n任意,则S为 $ \frac{4}{3} T $
这样的精确理论是希腊数学的特征之一,但在17、18世纪的近代早期数学,不得不去那里,甚至在19世纪中叶,它也被重建了。上面的阿基米德考察法在解析概论上很重要,所以让我详细说明一下。上面公式可得
$ | S - \frac{4}{3} T | < \frac{2T}{3} \cdot \frac{1}{4^{n}} $
这样 $ | S - \frac{4}{3} T | = 0 $,从而 $ S = \frac{4}{3} T $,这样S是T的定数,n是任意自然数。现在左边的定数写成 $ \epsilon $,右边定数 $ \frac{2}{3} T $用a表示,$ \epsilon \ge 0, a > 0, 4^{n} > n $,则
$ \epsilon < \frac{a}{n} $
这里 $ \epsilon = 0 $的话,它基于以下原理
$ \epsilon, a $为正数,$ n \epsilon > a $成立的自然数n存在。如果我们赞同这个原则,我们从 $ \epsilon > 0 $则有这样的n
$ \epsilon < \frac{a}{n}, \text{ 从而} n \epsilon < a $
这与阿基米德原则矛盾,则 $ \epsilon > 0 $的假设不成立,然而 $ \epsilon \ge 0 $,则 $ \epsilon = 0 $
阿基米德的原则包含在实数的连续性中,如果阿基米德原则不成立,则所有的自然数 $ n \le \frac{a}{\epsilon} $。即所有的自然数的集合有界,从而这样的集合的上限为s,从而有自然数 $ s - 1 < n \le s $,从而s < n + 1,n + 1也是自然数,这样矛盾,则不得不承认阿基米德原则
微分法之后的求积法
上面的求积法很巧妙,古代阿基米德开始使用,但是,它只能用于抛物线,在18世纪,这样的求积问题任何人都可以通过以下方法轻松地解决:
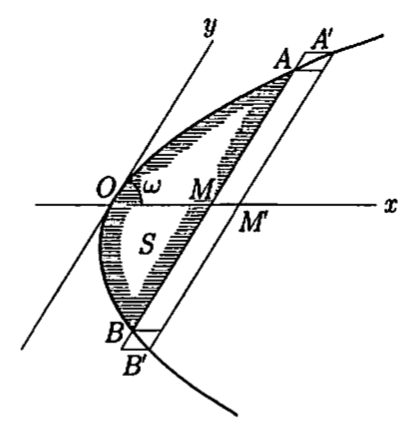
和之前一样,抛物线方程为
$ y^{2} = cx $
面积S为OM = x地函数S(x),使用如下记号
$ \bigtriangleup S = \text{面积}(ABB^{\prime}A^{\prime}) $
这样的面积被 $ AB, A^{\prime}B^{\prime} $夹着,底为两个平行四边形面积 $ AB \cdot \bigtriangleup x \cdot \sin{\omega} $和 $ A^{\prime}B^{\prime} \cdot \bigtriangleup x \cdot \sin{\omega} $中间(AM = y):
$ 2y \sin{\omega} \cdot \bigtriangleup x < \bigtriangleup S < 2(y+ \bigtriangleup y) \sin{\omega} \cdot \bigtriangleup x $
$ 2y \sin{\omega} < \frac{\bigtriangleup S}{\bigtriangleup x} < 2y \sin{\omega} + 2 \sin{\omega} \cdot \bigtriangleup y $
这样 $ \triangle x > 0 $就完了,$ \triangle x < 0 $也一样,只是不等号改变了方向。这样 $ \triangle x \to 0 $时 $ \triangle y \to 0 $,这样
$ \frac{dS}{dx} = 2y \sin{\omega} = 2 \sin{\omega} \cdot \sqrt{cx} $
然而
$ \frac{dx^{\frac{3}{2}}}{dx} = \frac{3}{2} \sqrt{x} $
这样
$ F(x) = \frac{4}{3} \sqrt{c} \cdot \sin{\omega} \cdot x^{\frac{3}{2}} $
如果你把
$ \frac{dF}{dx} = \frac{dS}{dx}, \qquad \text{即} \frac{d(F - S)}{dx} = 0 $
这样F - S为定数,x = 0时F(0) = 0, S = 0,这样定数为0,S = F。即
$ S(x) = \frac{4}{3} \sqrt{c} \cdot \sin{\omega} \cdot x^{\frac{3}{2}} $
这就是要求的面积。这样同阿基米德的计算结果一致,实际上
$ \begin{aligned} S(x) &= \frac{4}{3} \cdot \sqrt{cx} \cdot x \sin{\omega} = \frac{4}{3} yx \sin{\omega} = \frac{4}{3} AM \cdot OM \cdot \sin{\omega} \\ &= \frac{4}{3} \cdot \frac{1}{2} AB \cdot OM \cdot \sin{\omega} = \frac{4}{3} \triangle OAB \end{aligned} $
用这样的方法,如下图所示的曲线y = f(x)与x轴之间的两条垂线夹着的面积S与上图相同,不限于抛物线
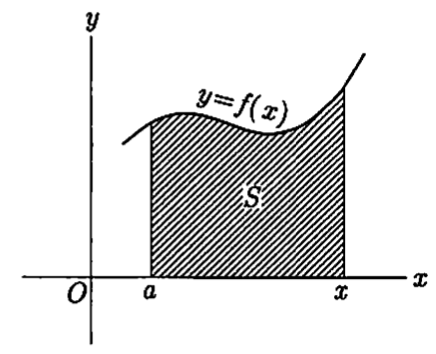
即f(x)为连续函数的话,$ \triangle x \to 0 $时,$ \triangle y \to 0 $,则
$ \frac{dS}{dx} = f(x) $
这样F(x)有
$ F^{\prime}(x) = f(x) $
如果函数是
$ \frac{d(S - F)}{dx} = 0 $
从而
$ S(x) - F(x) = C $
而x = a时S(a) = 0,则C = -F(a)。则
$ S(x) = F(x) - F(a) $
如果F(x)取自初等函数的范围,则 $ F^{\prime}(x) $也是初等函数,为f(x)。曲线y = f(x)求相关面积,这样的F(x)有无数个,这样求积问题解决了
这是微积分发现所带来的奇迹
给定f(x),F(x)是f(x)的导函数,$ F^{\prime}(x) = f(x) $,F(x)被称为f(x)的原函数,使用积分符号,则
$ F(x) = \int f(x)dx $
如果原始函数是作为初等函数获得的,则可以用一些公式获得,但是通过这样的手段
$ \int \frac{dx}{\sqrt{1 - x^{4}}}, \qquad \int \frac{dx}{\sqrt{\cos{x}}} $
找到这样一个看似简单的函数的原函数并不容易,如果是这样,是否总有一个连续函数的原函数?
前面我们用面积来得到原始函数,如果原始函数的存在很重要,那么面积的可能性也是一样的。我们谈到了面积、体积,但面积、体积意味着什么呢?
这些问题源自于19世纪以后,实现了比较安全的解析学的建立
定积分
解决上一节提到的问题是积分法的任务,我们想把考虑的范围放在连续函数中,但这在应用中产生了一个问题。例如,当有一些不连续点的时候,所以我们不能排除这种情况。因此,我们暂时稍微扩大考虑的范围,只假设函数的有界性
$ \left. \begin{array}{c|c} \hline f(x) = F^{\prime}(x) & F(x) \\ \hline x^{\alpha} \qquad (\alpha \ne 1) & \frac{x^{\alpha+1}}{\alpha + 1} \\ \frac{1}{x} \qquad (x \ne 0) & \log{ | x | } \\ \frac{1}{1+x^{2}} & \arctan{x} \\ \frac{1}{1 - x^{2}} \qquad (x \ne \pm 1) & \frac{1}{2} \log{| \frac{1+x}{1-x} | } \\ \frac{1}{x^{2}-1} \qquad (x \ne \pm 1) & \frac{1}{2} \log{ | \frac{x-1}{x+1} | } \\ \frac{1}{\sqrt{1-x^{2}}} \qquad (| x | < 1) & \arcsin{x} \\ \frac{1}{\sqrt{x^{2}-1}} \qquad (| x | > 1) & \log{ | x + \sqrt{x^{2} - 1} |} \\ \frac{1}{\sqrt{x^{2}+1}} & \log{(x + \sqrt{x^{2}+1})} \\ \sqrt{1-x^{2}} \qquad (| x | \le 1) & \frac{1}{2} (x \sqrt{1 - x^{2}} + \arcsin{x}) \\ \sqrt{x^{2} - 1} \qquad (| x | \ge 1) & \frac{1}{2} (x \sqrt{x^{2} - 1} - \log{| x + \sqrt{x^{2} - 1} |}) \\ \sqrt{x^{2} + 1} & \frac{1}{2} (x \sqrt{x^{2}+1} + \log{(x + \sqrt{x^{2}+1})}) \\ e^{x} & e^{x} \\ a^{x} \qquad (a > 0, a \ne 1) & \frac{a^{x}}{\log{a}} \\ \sin{x} & -\cos{x} \\ \cos{x} & \sin{x} \\ \frac{1}{\sin^{2}{x}} & - \cot{x} \\ \frac{1}{\cos^{2}{x}} & \tan{x} \\ \tan{x} & - \log{ | \cos{x} |} \\ \cot{x} & \log{ | \sin{x} | } \end{array} \right. $
Legendre球函数
应用分部积分法,考察下面的问题。关于n-1次以下的多项式Q(x)
$ \int^{b}_ {a} Q(x)P_ {n}(x) dx = 0 $
求这样的n次多项式 $ P_ {n}(x) $
顺便说一句,如果这样的多项式存在,忽略常数因子的差异,则只有一个。事实上,如果 $ \varphi(x), \psi(x) $为符合的多项式,$ \varphi(x) - c \psi(x) $为n-1次,c为常数,取$ Q(x) = \varphi(x) - c \psi(x) $,假定
$ \int^{b}_ {a} Q(x)\varphi(x) dx = 0, \qquad \int^{b}_ {a} Q(x)\psi(x) dx = 0 $
从而
$ \int^{b}_ {a} (\varphi(x) - c \psi(x))Q(x)dx = 0 $ 即 $ \int^{b}_ {a} (Q(x))^{2}dx = 0 $
Q(x)连续,区间[a, b]中Q(x) = 0。因为Q(x)为多项式,则Q(x) = 0。这样 $ \varphi(x) = c \psi(x) $
现在证明适合问题条件的多项式 $ P_ {n}(x) $实际存在如下
多项式的原函数比多项式阶次高1,则n阶多项式 $ P_ {n}(x) $是2n次多项式F(x)的第n阶导数。即 $ F^{(n)}(x) = P_ {n}(x) $,这样
$ \int^{b}_ {a} QF^{(n)}dx = [QF^{(n-1)} - Q^{\prime}F^{(n-2)} + \cdots \pm Q^{(n-1)}F]^{b}_ {a} = 0 $
这样
$ F(a) = F^{\prime}(a) = \cdots = F^{(n-1)}(a) = 0 $
$ F(b) = F^{\prime}(b) = \cdots = F^{(n-1)}(b) = 0 $
满足该条件,这样的2n次多项式
$ F(x) = (x - a)^{n} (x - b)^{n} $
适合条件,C为任意常数,有
$ P_ {n}(x) = C \frac{d^{n}}{dx^{n}} (x - a)^{n} (x - b)^{n} $
区间为[-1, +1]时
$ P_ {n}(x) = \frac{1}{2^{n} \cdot n!} \frac{d^{n}}{dx^{n}} (x^{2} - 1)^{n} $
为Lengendre球函数。$ (x^{2} - 1)^{n} $展开
$ P_ {n}(x) = \sum^{[\frac{n}{2}]}_ {k=0} \frac{(-1)^{k}}{2^{k}} \frac{1 \cdot 3 \cdot 5 \cdots (2n - 2k - 1)}{k! (n-2k)!} x^{n-2k} $
例如
$ P_ {0}(x) = 1, \qquad P_ {1}(x) = x, \qquad P_ {2}(x) = \frac{1}{2} (3x^{2} - 1), \qquad P_ {3}(x) = \frac{1}{2} (5x^{3} - 3x) $
$ P_ {4}(x) = \frac{1}{8} (35x^{4} - 30x^{2} + 3), \qquad P_ {5}(x) = \frac{1}{8} (63x^{5} - 70x^{3} + 15x) $
以下 $ P_ {n}(x) $的二、三个性质叙述如下
(1) $ P_ {n}(x) $n是奇数时是奇函数,n是偶数时是偶函数
(2) $ P_ {n}(1) = 1, \qquad P_ {n}(-1) = (-1)^{n} $
证明
$ \begin{aligned} P_ {n}(x) &= \frac{1}{2^{n}n!} \frac{d^{n}}{dx^{n}}(x-1)^{n}(x+1)^{n} \\ &= \frac{1}{2^{n}n!} \left\{ \frac{d^{n}(x - 1)^{n}}{dx^{n}} (x+1)^{n} + n \frac{d^{n-1}(x-1)^{n}}{dx^{n-1}} \frac{d(x+1)^{n}}{dx} + \cdots + (x-1)^{n} \frac{d^{n}(x+1)^{n}}{dx^{n}} \right\} \end{aligned} $
最开始和最后的一项跟其他项用(x-1)(x+1)分割,有
$ P_ {n}(x) = \frac{1}{2^{n}} (x+1)^{n} + \frac{1}{2^{n}}(x-1)^{n} + (x-1)(x+1)G(x) $
G(x)为多项式。这里用x=1和x=-1带入得
(3)
$ \int^{1}_ {-1}P_ {n}(x)^{2}dx = \frac{2}{2n+1} $
$ \int^{1}_ {-1}P_ {m}(x)P_ {n}(x) dx = 0, \qquad (m \ne n) $
证明 $ m \ne n $时通过 $ P_ {n}(x) $的定义就明白
这样
$ P_ {n}P_ {n+1} |^{+1}_ {-1} = \int^{1}_ {-1}P_ {n}P^{\prime}_ {n+1}dx + \int^{1}_ {-1}P^{\prime}_ {n}P_ {n+1}dx $
左边根据(2)得2,右边的第二个积分 $ P^{\prime}_ {n} $为比n+1次低,则
$ 2 = \int^{+1}_ {-1}P_ {n}P^{\prime}_ {n+1}dx $
根据(1)的 $ P_ {n}(x) $的 $ x^{n} $的系数为 $ \frac{2n (2n-1) \cdots (n+1)}{2^{n} \cdot n!} $,则 $ P^{\prime}_ {n+1}(x) $关于 $ x^{n} $的系数为
$ \frac{(2n+2)(2n+1)\cdots (n+2)}{2^{n+1}(n+1)!} \cdot (n+1) $
则
$ P^{\prime}_ {n+1}(x) = (2n+1)P_ {n}(x) + Q(x) $
Q(x)为n-1次以下的多项式。两边关于 $ P_ {n}(x) $积分
$ \int^{+1}_ {-1}P_ {n}P^{\prime}_ {n+1}dx = (2n+1) \int^{+1}_ {-1}P^{2}_ {n}dx $
则有
$ 2 = (2n+1) \int^{+1}_ {-1}P^{2}_ {n} dx $
(4) 循环公式
$ (n+1)P_ {n+1}(x) - (2n+1)x P_ {n}(x) + nP_ {n-1}(x) = 0. \qquad (n \ge 1) $
证明:$ P_ {n}, P_ {n+1} $最高次项的系数比较得
$ P_ {n+1} - \frac{2n+1}{n+1}x P_ {n} $
从(1)得到n-1次以下的多项式。则
$ (n+1)P_ {n+1} - (2n+1)xP_ {n} = \alpha P_ {n-1} + Q $
系数 $ \alpha $适当确定,Q为n-2次以下的多项式。这样Q两边积分 $ \int^{1}_ {-1}Q^{2} dx = 0 $,从而Q = 0。系数 $ \alpha $确定的话通过x = 1取,这样,由(2)
$ n + 1 - (2n+1) = \alpha $ 这样 $ \alpha = -n $
$ P^{\prime}_ {n} $相关公式有
$ (1 - x^{2})P^{\prime}_ {n}(x) + nxP_ {n}(x) - nP_ {n-1}(x) = 0 $
(5) $ P_ {n}(x) = 0 $的根都是在-1和+1之间的实数。这样的单根,被$ P_ {n-1}(x) = 0 $的根隔离。即 $ P_ {n-1}(x) = 0 $夹在 $ P_ {n}(x) $的根之间
$ P_ {n}(x)(n \ge 1) $ 在 -1 和 +1 之间有n个单根,从最开始的公式有Rolle定理。$ P_ {n}(x), P_ {n-1}(x) $的根的配置是(2)。$ P_ {n}(x) $的根 $ x_ {1} $对应 $ P^{\prime}_ {n}(x_ {1}), P_ {n-1}(x_ {1}) $的符号相同。$ P_ {n}(x) $相邻的两个根 $ x_ {1}, x_ {2} $,$ P^{\prime}_ {n}(x_ {1}), P^{\prime}_ {n}(x_ {2}) $有相反的符号,$ P_ {n-1}(x_ {1}), P_ {n-1}(x_ {2}) $有相反的符号,从而 $ [x_ {1}, x_ {2}] $内$ P_ {n-1}(x) $的根至少有一个,考虑实根的个数,可以看出刚好只有一个
(6) 关于微分方程的母函数,$ u = (x^{2} - 1)^{n} $
$ (x^{2} - 1)u^{\prime} = 2nxu $
这里n+1次微分
$ (x^{2} - 1)u^{(n+2)} + 2(n+1)xu^{(n+1)} + n(n+1)u^{(n)} = 2nxu^{(n+1)} + 2n(n+1)u^{(n)} $
即
$ (x^{2} - 1)u^{(n+2)} + 2xu^{(n+1)} - n(n+1)u^{(n)} = 0 $
由于$ u^{(n)} = CP_ {n}(x) $,$ P_ {n}(x) $的微分方程的解为
$ (x^{2} - 1)y^{\prime \prime} + 2xy^{\prime} - n(n+1)y = 0 $
不定积分的计算
(I) F作为有理函数
$ \int F(\cos{x}, \sin{x}) dx $
进行考察,变量变换
$ t = \tan{\frac{x}{2}} $
有
$ \cos{x} = \frac{1 - t^{2}}{1 + t^{2}}, \qquad \sin{x} = \frac{2t}{1+t^{2}} $
则
$ t = \frac{\sin{x}}{1 + \cos{x}} $
x从 $ -\pi $到 $ \pi $变化,t则从 $ -\infty $到 $ + \infty $单调增大,这样
$ x = 2 \arctan{t}, dx = \frac{2dt}{1+t^{2}} $
从而
$ \int F(\cos{x}, \sin{x}) dx = \int F( \frac{1 - t^{2}}{1 + t^{2}}, \frac{2t}{1+t^{2}}) \frac{2dt}{1+t^{2}} $
例1
$ \int \frac{dx}{\sin{x}} = \int \frac{1+t^{2}}{2t} \cdot \frac{2dt}{1+t^{2}} = \int \frac{dt}{t} = \log{| t |} = \log{| \tan{\frac{x}{2}} |}, \qquad (x \ne n\pi, n = 0, \pm 1, \cdots) $
例2
$ \int \frac{dx}{a \cos^{2}{x} + b \sin^{2}{x}} = \int \frac{dt / (1+t^{2})}{(a+bt^{2})/(1+t^{2})} = \int \frac{dt}{a+bt^{2}}, \qquad (t = \tan{x}) $
a > 0, b > 0的话 $ t = \sqrt{ \frac{a}{b}} \tau $
$ \int \frac{dt}{a+bt^{2}} = \frac{1}{\sqrt{ab}} \int \frac{d \tau}{1 + \tau^{2}} = \frac{1}{\sqrt{ab}} \arctan{\tau} $
a > 0, b < 0的话,b用-b替换得
$ \int \frac{dx}{a \cos^{2}{x} - b \sin^{2}{x}} = \int \frac{dt}{a - b t^{2}} = \frac{1}{\sqrt{ab}} \int \frac{d \tau}{1 - \tau^{2}} = \frac{1}{2 \sqrt{ab}} \log{ | \frac{1 + \tau}{1 - \tau} |}, $
$ \left( a > 0, b > 0; t = \tan{x}, \tau = \sqrt{\frac{b}{a}} t. \right) $
(II) F(x, y)作为有理式
$ \int F(x, \sqrt{ax^{2} + bx + c}) dx $
开考察,做变量变换,消去二次式里的一次项,根据a的正负有形如 $ \sqrt{x^{2} \pm p^{2}} $或 $ \sqrt{p^{2} - x^{2}} $的平方根,这样 $ x = p \tan{\theta}, x = p \sec{\theta} $或 $ x = p \sin{\theta} $,这样回到(I)的情况,从而是有理化的
不过也可以不经过三角函数,直接用代数变换有理化,现在上述平方根用y记,则
$ y^{2} = ax^{2} + bx + c $
这个是二次曲线,通过曲线上任意一点 $ (x_ {0}, y_ {0}) $的截线
$ y - y_ {0} = t(x - x_ {0}) $
在 $ (x_ {0}, y_ {0}) $外另一点(x, y)和曲线相交。从而交点(x, y)和t一一对应,计算坐标x,y的话,$ x = \varphi(t), y = \psi(t) $的有理式
$ \int F(x, \sqrt{ax^{2} + bx + c}) dx = \int F(\varphi(t), \psi(t)) \varphi^{\prime}(t) dt $
即问题的积分变换有理化
(1) 特别地二次式根有的情况下
$ y^{2} = ax^{2} + bx + c = a(x - \alpha)(x - \beta) \qquad (\alpha \ne \beta) $
时,上述的 $ (x_ {0}, y_ {0}) $作为 $ (\alpha, 0) $,有
$ y = t(x - \alpha) $
变换得
$ t = \sqrt{\frac{a(x - \beta)}{x - \alpha}} $
(2) 没有实根时,取a > 0,a > 0时通常要转换
$ y = \pm \sqrt{a} x + t $
即
$ t = \mp \sqrt{a}x + \sqrt{ax^{2} + 2bx + c} $
可有理化
这样,双曲线的截线和双曲线的渐近线平行,截线和双曲线交于一点(x, y),该坐标用变量t来有理式表达
根据基本不定积分
$ \int \frac{dx}{\sqrt{x^{2} \pm 1}} = \log{ |x + \sqrt{x^{2} \pm 1} |} $
有
$ t = x + \sqrt{x^{2} - 1} $
和
$ t^{-1} = x - \sqrt{x^{2} - 1} $
从而
$ 2x = t + t^{-1}, \qquad 2 \sqrt{x^{2} - 1} = t - t^{-1}, 2dx = (1 - t^{-2})dt $
则
$ \begin{aligned} \int \frac{dx}{\sqrt{x^{2} - 1}} &= \int \frac{(1 - t^{-2})dt}{t - t^{-1}} = \int \frac{dt}{t} = \log{ | t | } \\ &= \log{ | x + \sqrt{x^{2} - 1} |} \end{aligned} $
同样的
$ t = -x + \sqrt{x^{2} + 1} $
和
$ \int \frac{dx}{\sqrt{x^{2} +1}} = \log{ (x + \sqrt{x^{2} + 1}) } $
上述(I)、(II)积分有理化的叙述,实际计算时,不必拘泥于上述一般方法。但不认识有理化的可能原因而盲目计算也不好,将无法控制计算
关于P(x)的 $ F(x, \sqrt{P(x)}) $,如果是没有平方因子的三次或四次多项式,其积分不是初等函数,是椭圆积分。如果P(x)是更高次数,则是超椭圆积分。当包含一个一次式的三个或更多平方根时也一样
(III) 二项微分的积分,如下
$ \int x^{m}(ax^{n} + b)^{q} dx $
m,n,q是有理数,牛顿已经考察过了,用 $ x^{n} = t $替换
$ \int t^{p} (at + b)^{q}dt, \qquad p = \frac{m+1}{n} - 1 $
p,q为有理数p + q为整数的话是有理函数的积分,q为整数,$ p = \frac{h}{k}, t = s^{k} $变化得
$ k \int s^{h+k-1}(as^{k} + b)^{q} ds $
如果q为正整数,最好从头开始展开$ (at + b)^{q} $。如果p为整数,at + b作为变量则回到前一种情况。如果p + q为整数,则 $ 1 / t $作为变量
除了这些情况,二项微分的不定积分不能用初等函数完成。在其原始形式中,只有当m,n,q是有理数,q或者 $ \frac{m+1}{n} $或者 $ \frac{m+1}{n} + q $是整数时不定积分才是可能的
例 $ \sin^{\mu}{x} \cos^{\upsilon}{x} $用 $ \sin{x} = \sqrt{t} $变换为二项微分 $ \frac{1}{2} t^{\frac{\mu-1}{2}} (1-t)^{\frac{\upsilon - 1}{2}} dt $。从而,$ \mu, \upsilon $为有理数,$ \mu $或则 $ \upsilon $为正或者负的奇数,或者 $ \mu + \upsilon $为偶数时,才可能有理化
$ \int \frac{dx}{\sqrt{\cos{x}}}, \mu = 0, \upsilon = \frac{1}{2} $ 不能有理化
定积分的近似计算
虽然已经证明了连续函数的不定积分的存在性,但一般不可能从不定积分的定积分计算出来,因为它只有在特殊情况下才能用已知函数表示。但是根据维尔斯特拉斯定理关于[a,b]的区间,跟连续函数f(x)一样的近似多项式P(x)存在,在[a,b]中
$ | f(x) - P(x) | < \epsilon $
作为 $ \int^{b}_ {a}f(x)dx $的近似值 $ \int^{b}_ {a}P(x)dx $,误差小于 $ \epsilon(b - a) $。实际上,对给定的 $ \epsilon $求P(x)很困难,但基于使用多项式的近似方法已经设计出了一种实用的计算方法。这里会描述Simpson方法及Gauss方法
三次式的积分 P(x)是三次以下的多项式
$ \int^{b}_ {a} P(x) dx = \frac{b - a}{6} \left\{ P(a) + P(b) + 4P(\frac{a+b}{2}) \right\} $
这个简单的计算问题,简单说明如下
为了简化,原点移动 $ \frac{a+b}{2} $,b - a = 2h替换得
$ \int^{h}_ {-h} P(x) dx = \frac{h}{3} \left\{P(h) + P(-h) + 4P(0) \right\} $
P(x)为 $ 1,x,x^{2}, x^{3} $的结合,这样带入上式中,有
$ 2h = \frac{h}{3}(1 + 1 + 4), \qquad 0 = \frac{h}{3}(h - h + 0), \qquad \frac{2}{3} h^{3} = \frac{h}{3}(h^{2} + h^{2} + 0), \qquad 0 = \frac{h}{3}(h^{3} - h^{3} + 0) $
现在最粗略的近似函数f(x)为x = a, x = b及 $ x = \frac{a+b}{2} $对二次式P(x)置换,积分计算得
$ \int^{b}_ {a} f(x)dx = \frac{b-a}{6} \{f(a) + f(b) + 4f(\frac{a+b}{2}) \} $
f(x)第四阶连续微分是可能,剩余项精确得
$ \int^{b}_ {a}f(x)dx = \frac{b-a}{6}\left\{ f(a) + f(b) + 4f(\frac{a+b}{2}) \right\} - \frac{(b-a)^{5}}{2^{5} \cdot 90}f^{(4)}( \xi) $
用b - a = 2h置换得
$ \varphi(h) = \int^{h}_ {-h} f(x) dx - \frac{h}{3}(f(h) + f(-h) + 4f(0)) $
作为h的函数,简单计算得
$ \varphi(0) = \varphi^{\prime}(0) = \varphi^{\prime \prime}(0) = 0 $
$ \varphi^{\prime \prime \prime}(h) = - \frac{h}{3} (f^{\prime \prime \prime}(h) - f^{\prime \prime \prime}(-h)) = - \frac{2h^{2}}{3} f^{(4)}(\xi), \qquad (-h < \xi < h) $
使用[0, h]区间 $ \varphi(h) $的Taylor公式
$ \varphi(h) = \frac{1}{2} \int^{h}_ {0} \frac{\varphi^{\prime \prime \prime}(x)}{x^{2}} x^{2}(h-x)^{2}dx $
使用平均值定理
$ \begin{aligned} \varphi(h) &= \frac{\varphi^{\prime \prime \prime}(\eta)}{2 \eta^{2}} \int^{h}_ {0} x^{2}(h-x)^{2}dx \qquad (0 < \eta < h) \\ &= - \frac{f^{(4)}(\xi^{\prime})}{3} [\frac{x^{5}}{5} - \frac{2hx^{4}}{4} + \frac{h^{2}x^{3}}{3} ]^{h}_ {0} \qquad (- \eta < \xi^{\prime} < \eta) \\ &= - \frac{f^{(4)}(\xi^{\prime})}{3} h^{5} (\frac{1}{5} - \frac{1}{2} + \frac{1}{3}) \\ &= - \frac{h^{5}}{90} f^{(4)}(\xi^{\prime}) \end{aligned} $
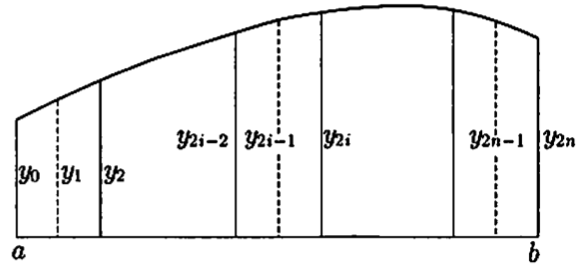
用Simpson方法对上面的式子,把区间[a, b]分成2n个等分,各分点对应f(x)的值为 $ y_ {0}, y_ {1}, y_ {2}, \ldots, y_ {2n} $,用 $ h = \frac{b-a}{2n} $置换,邻接 $ y_ {2i-1} $的二个区间积分 $ \int f(x)dx $的近似值为
$ \frac{h}{3} (y_ {2i-2} + y_ {2i} + 4y_ {2i-1}) $
$ i = 1, 2, \ldots, n $,统计得
$ \int^{b}_ {a} f(x)dx = \frac{h}{3} \{y_ {0} + y_ {2n} + 2(y_ {2} + y_ {4} + \cdots + y_ {2n-2}) + 4(y_ {1} + y_ {3} + \cdots + y_ {2n-1}) \} $
这个就是Simpson公式
但取剩余项统计得
$ R = - \frac{h^{5}}{90} \sum^{n}_ {i=1}f^{(4)}(\xi_ {i}) $
使用平均值 $ \frac{1}{n} \sum f^{(4)}(\xi_ {i}) = f^{(4)}(\xi), (a < \xi < b) $
$ R = - \frac{nh^{5}}{90} f^{(4)}(\xi) $
使用 $ nh = \frac{b-a}{2} $
$ R = - \frac{(b-a)f^{(4)}(\xi)}{180} h^{4} $
n越大,则h越小,这样就是Simpson公式的误差的界限
例子 从$ \frac{\pi}{4} = \int^{1}_ {0} \frac{dx}{1+x^{2}} $计算 $ \pi $的近似值。n = 5,h = 0.1
$ \frac{\pi}{4} = \frac{0.1}{3} \{ 1 + \frac{1}{2} + 2(\frac{1}{1.04} + \frac{1}{1.16} + \frac{1}{1.36} + \frac{1}{1.64}) + 4(\frac{1}{1.01} + \frac{1}{1.09} + \frac{1}{1.25} + \frac{1}{1.49} + \frac{1}{1.81}) \} $
用逆数表七位小数计算,得如下结果
$ \pi = 3.14159288 $
对球函数P(x)用Gauss方法 首先通过变量的变换把积分区域变为[-1, 1],$ f(x) = P_ {n}(x)Q(x) + \varphi(x) $,商Q和余数 $ \varphi(x) $有以下的等式
$ \int^{1}_ {-1} Q(x)P_ {n}(x) dx = 0 $
从而
$ \int^{1}_ {-1}f(x)dx = \int^{1}_ {-1}\varphi(x)dx $
现在 $ P_ {n}(x) $的根为 $ x_ {\upsilon}(\upsilon = 1,2,\ldots, n) $,根据Lagrange补充公式
$ \varphi(x) = \sum^{n}_ {\upsilon=1} \frac{\varphi(x_ {\upsilon})}{P^{\prime}_ {n}(x_ {\upsilon})} \frac{P_ {n}(x)}{x - x_ {\upsilon}} = \sum^{n}_ {\upsilon=1} \frac{f(x_ {\upsilon})}{P^{\prime}_ {n}(x_ {\upsilon})} \frac{P_ {n}(x)}{x - x_ {\upsilon}} $
则
$ \int^{1}_ {-1}f(x)dx = \sum^{n}_ {\upsilon=1} \frac{f(x_ {\upsilon})}{P^{\prime}_ {n}(x_ {\upsilon})} \frac{P_ {n}(x)}{x - x_ {\upsilon}} = \sum^{n}_ {\upsilon=1} \frac{f(x_ {\upsilon})}{P^{\prime}_ {n}(x_ {\upsilon})} \frac{P_ {n}(x)}{x - x_ {\upsilon}} $
由
$ p_ {\upsilon} = \frac{1}{P^{\prime}_ {n}(x_ {\upsilon})} \int^{1}_ {-1} \frac{P_ {n}(x)}{x - x_ {\upsilon}} dx $
置换得
$ \int^{1}_ {-1}f(x)dx = \sum^{n}_ {\upsilon=1}p_ {\upsilon}f(x_ {\upsilon}) $
这里 $ x_ {\upsilon} $只与 $ p_ {\upsilon}, P_ {n}(x) $有关,它们的值有一个表
例如,$ n = 3, \qquad x_ {1}, x_ {3} = \mp \frac{\sqrt{15}}{5}, \qquad p_ {1} = p_ {3} = \frac{5}{9} $
$ x_ {2} = 0, p_ {2} = \frac{8}{9} $
任意f(x)的五次式
$ \int^{1}_ {-1}f(x)dx = \frac{5}{9} \left\{ f( - \frac{\sqrt{15}}{5}) + f(\frac{\sqrt{15}}{5}) \right\} + \frac{8}{9} f(0) $
当有任意的连续函数F(x)时,关于区间[-1,1] $ 有x_ {\upsilon} $和其他n个点,一共2n个点跟F(x)值相等的2n-1次以下的多项式f(x),这样把F(x)带入,$ \int^{1}_ {-1}F(x) $的近似值为 $ \int^{1}_ {-1}f(x)dx $,得
$ \int^{1}_ {-1}F(x)dx = \sum^{n}_ {\upsilon=1}p_ {\upsilon} F(x_ {\upsilon}) $
使用n个 $ F(x_ {\upsilon}) $值,这样的近似值计算为Gauss方法的特点
有界变动的函数
之前介绍了曲线函数,这里给定区间[a, b]的函数f(x),这个区间
$ (\Delta) \qquad a = x_ {1} < x_ {2} < \cdots < x_ {n} < x_ {n+1} = b $
对于点 $ x_ {i} $的小区间进行分割
$ \upsilon_ {\Delta} = \sum^{n}_ {i=1} | f(x_ {i+1}) - f(x_ {i}) | $
所有关于 $ \upsilon_ {\Delta} $的分割 $ \Delta $有界的话,这样的上限设为V,这是[a, b]区间的f(x)总变动量,f(x)则称为[a, b]上有界变动的函数
这时,区间内任一点x,从 $ | f(x) - f(a) | \le V $有 $ | f(x) - f(a) | + | f(b) - f(x) | \le V $
对 $ f(x_ {i+1}) - f(x_ {i}) $,正的和负的总和记为$ p_ {\Delta}, -n_ {\Delta} $,这样
$ \upsilon_ {\Delta} = p_ {\Delta} _ n_ {\Delta}, \qquad f(b) - f(a) = p_ {\Delta} - n_ {\Delta} $
这样有界变动的时候,$ p_ {\Delta}, n_ {\Delta} $也有界。这样的上限记为P, N
V = P + N, f(b) - f(a) = P - N
取[a, b]内一点x,区间[a, x]的f(x)也有界变动,[a, x]对应的V、P、N的x的函数存在,写为V(x)、P(x)、 N(x)
V(x) = P(x) + N(x), f(x) - f(a) = P(x) - N(x)
定理38 有界变动函数等于两个有界递增函数之差
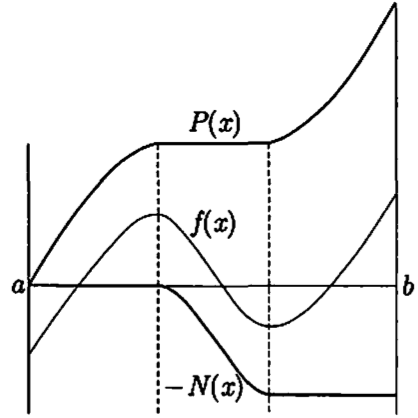
关于f(x) = f(a) + P(x) - N(x),P(x), N(x)是特定的单调函数,一般地,$ \varphi(x), \psi(x) $是有界的增大函数的话,它的差 $ f(x) = \varphi(x) - \psi(x) $有界变动,f(x)的变动不超过 $ \varphi, \psi $变动之和:$ V(x) \le (\varphi(x) - \varphi(a)) + (\psi(x) - \psi(a)) $
$ \varphi(x), \psi(x) $的和和积是有界变动。商 $ \varphi(x) / \psi(x) $在[a, b]上 $ | \psi(x) | > m > 0 $的话,也是有界变动。对积
$ \begin{aligned} | \varphi(x_ {1})\psi(x_ {1}) - \varphi(x_ {2})\psi(x_ {2}) | &= | \psi(x_ {1})(\varphi(x_ {1}) - \varphi(x_ {2})) + \varphi(x_ {2})(\psi(x_ {1}) - \psi(x_ {2})) | \\ &= \le M(| \varphi(x_ {1}) - \varphi(x_ {2}) | + | \psi(x_ {1}) - \psi(x_ {2}) |) \end{aligned} $
$ (| \varphi(x) | < M, | \psi(x) | < M) $,商也一样
从而,有界变动函数的和、差、积也是有界变动
有界函数f(x)的全变动V(x)是关于区间的加法。总之,区间[a, b]关于c点分割成[a, c]和[c, b]时,区间的全变动可写为
V(a, b) = V(a, c) + V(c, b)
同样对P, N
P(a, b) = P(a, c) + P(c, b), N(a, b) = N(a, c) + N(c, b)
c作为区间左端的话
N(c, x) = P(a, x) - P(a, c)
N(c, x) = N(a, x) - N(a, c)