Table of Contents
序为n的Farey系列 $ \Im_ {n} $是在0和1之间不可约的分数递增序列,其分母不超过n。则h / k 属于 $ \Im_ {n} $如果
$ 0 \le h \le k \le n, \qquad (h, k) = 1 $
0和1之间包含 $ \frac{0}{1}, \frac{1}{1} $。例如,$ \Im_ {5} $为
$ \frac{0}{1}, \frac{1}{5}, \frac{1}{4}, \frac{1}{3}, \frac{2}{5}, \frac{1}{2}, \frac{3}{5}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{1}{1} $
定理 如果 $ h / k, h^{\prime} / k^{\prime} $是 $ \Im_ {n} $中两个连续的项,则
$ kh^{\prime} - hk^{\prime} = 1 $
定理 如果 $ h / k, h^{\prime \prime} / k^{\prime \prime}, h^{\prime} / k^{\prime} $是 $ \Im_ {n} $中三个连续的项,则
$ \frac{h^{\prime \prime}}{k^{\prime \prime}} = \frac{h + h^{\prime}}{k + k^{\prime}} $
定理 如果 $ h / k, h^{\prime} / k^{\prime} $是 $ \Im_ {n} $中两个连续的项,则
$ k + k^{\prime} > n $
则它们的中位数
$ \frac{h + h^{\prime}}{k + k^{\prime}} $
在区间
$ (\frac{h}{k}, \frac{h^{\prime}}{k^{\prime}}) $
定理 如果n > 1,则 $ \Im_ {n} $中连续两项没有相同的分母
Minkowski的一个定理 如果P和Q是 $ \Lambda $的点,$ P^{\prime} $和 $ Q^{\prime} $是P和Q关于原点的对称点,且我们添加平行定理的平行四边形J三个平行基于 $ OQ, OP^{\prime} $、基于 $ OP^{\prime}, OQ^{\prime} $、基于$ OQ^{\prime}, OP $,我们获得一个平行四边形K其中心是原点,面积 $ 4 \delta $是J的4倍。如果 $ \delta $有值1(它的至少可能值)有 $ \Lambda $的点在K的边界上,但除了O,都在内部。如果 $ \delta > 1 $,则有 $ \Lambda $的点,不是O,在K内部。这是著名的Minkowski定理的一个特殊例子,其断言拥有相同的属性,不只是任意平行四边形对原点对称,而且凸区域跟原点对称
一个开放的区域R是一个点的集合有属性(1) 如果P属于R,则平面的所有点有效靠近P的属于R,(2)R的任意两点被一个完全在R中连续的曲线相交。我们可表达(1)为对R中任意点是R中的内点。这样圆的内部或一个平行四边形是一个开放区域。R的边界C是点集,其是R的限制点但不属于R。这样一个圆的边界是它的周长。一个闭区域 $ R^{* } $是一个开区域R及其边界。我们只考虑有界区域
有凸区域的两个自然定义,其显示是等价的。首先,我们可说R(或 $ R^{* } $)是凸的如果R的任意弦上的每个点,例如,任意线交R的两个点,属于R。第二,我们可说R(或$ R^{* } $)是凸的如果它可能,通过C的每个点P,画至少一条线l使得整个R位于l的一边。这样一个圆和一个平行四边形是凸的。对圆,l是P点的切线,而对平行四边形l是除了顶点的一条边
容易证明两个定义相当。假设第一个R是凸的根据第二个定义,则P和Q属于R,且PQ的一个点S不属于。则有C的一个点T在PS上,且一条线通过T整个离开R的一条边;因此所有点有效靠近P或Q属于R,这是矛盾的
第二,假设R是凸的根据第一个定义且P是C的一个点;考虑集合L线交P到R的点。如果$ Y_ {1}, Y_ {2} $是R的点,且Y是 $ Y_ {1}Y_ {2} $的一个点,则Y是R的一个点且PY是L的一条线。因此有一个角APB,属于L。如果 $ APB > \pi $,则有R上的点D, E使得DE穿过P点,P属于R不属于C,矛盾。因此 $ APB \le \pi $。如果 $ APB = \pi $,则AB是一条线l,如果 $ APB < \pi $,则任意线穿过P,在角之外,是一条线
定理(Minkowski定理) 任意对O对称的凸区域R,且面积大于4,包含不同于O的 $ \Lambda $点
Minkowski定理的证明
定理 假设 $ R_ {O} $是包含O的一个开放区域,$ R_ {P} $是congruent且对 $ \Lambda $的任意点P有相似区域,且区域 $ R_ {P} $互相不覆盖。则 $ R_ {O} $面积不超过1
如果 $ R_ {O} $是平方,边界为线 $ X = \pm \frac{1}{2}, y = \pm \frac{1}{2} $,则 $ R_ {O} $的面积为1,且区域$ R_ {P} $,及它们的边界,覆盖平面。我们将给出精确地证明如下
假设 $ \Delta $是 $ R_ {O} $的面积,且A是从O到点 $ C_ {O} $的最大距离;且我们考虑 $ (2n+1)^{2} $区域 $ R_ {P} $对应 $ \Lambda $的点,其坐标不大于n。所有这些区域位于平方其边平行于坐标轴,且从O有距离n + A。因此(因为区域不覆盖)
$ (2n+1)^{2} \Delta \le (2n+2A)^{2}, \qquad \Delta \le \left(1 + \frac{A - \frac{1}{2}}{n + \frac{1}{2}} \right)^{2} $
当n趋于无穷时我们有结果
现在证明Minkowski定理是容易的,Minkowski本人给出了两个证明,基于凸性的两个定义
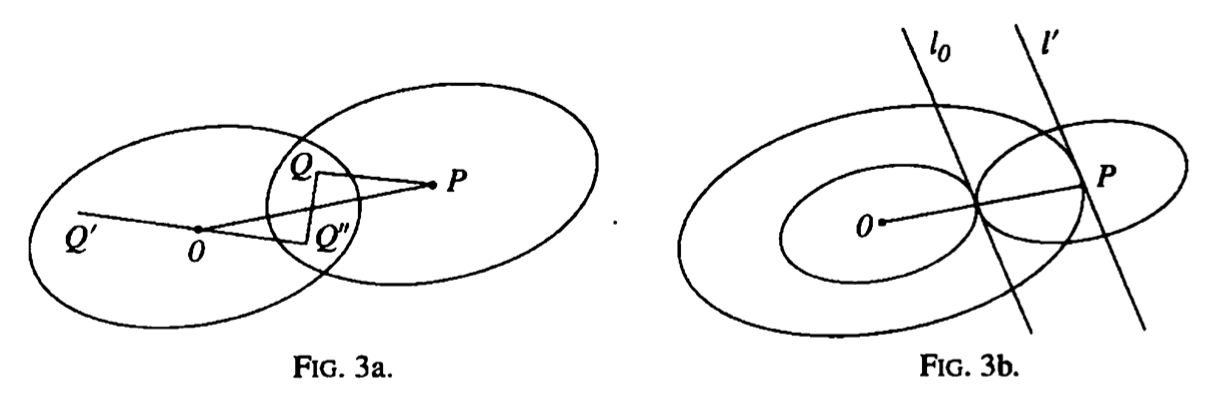
(1)对第一个定义,假设 $ R_ {O} $关于O压缩R到它线性维度的结果。则 $ R_ {O} $的面积大于1,这样之前定理的两个 $ R_ {P} $区域覆盖,有一个lattice点P使得 $ R_ {O}, R_ {P} $覆盖。设Q(下图3a)为 $ R_ {O}, R_ {P} $公共的点,如果$ OQ^{\prime} $相等且平行于PQ,且 $ Q^{\prime \prime} $是O中 $ Q^{\prime} $的象,则 $ Q^{\prime} $,且因此 $ Q^{\prime \prime} $,位于 $ R_ {O} $中;且因此,通过凸性的定义,$ QQ^{\prime} $的中点位于 $ R_ {O} $中。但该点是OP的中点,且因此P在R中