Table of Contents
6个人的聚会
我们现在看一个6个人聚会的例子。设G为一个图形,我们引入如下的记号:$ \omega(G) $记为一个完全子图的最大顶点数,且 $ \alpha(G) $为G中一个独立集合的最大顶点数,即集合中两个顶点之间没有被一条边连接
定理
设G为一个至少6个顶点的图,则 $ \alpha(G) \ge 3 $ 或 $ \omega(G) \ge 3 $
证明 让我们任意选择G中一个顶点且让我们把它记为u。设 $ A \subseteq V(G) \ \{u\} $为不连接到u的顶点集合;形式为 $ A = \{v \in V(G): v \ne u, \{u, v\} \notin E(G) \} $。设 $ B = V(G) \ A \ \{u \} $ 包含连接到u的顶点。因为 $ | V(G) | \ge 6 $,A、B集合中必须至少有一个有3个元素。我们现在区分两种情况
- $ | A | \ge 3 $。设A包含顶点x, y, z。如果每两个形成G的一条边,则 $ \{x, y, z\} $确定为一个三角形,例如,一个完全子图显示 $ \omega(G) \ge 3 $。否则,如果,例如,$ \{x, y\} \notin E(G) $,则 $ \{x, y, z \} $在G中是一个独立集合,且这样 $ \alpha(G) \ge 3 $
- $ | B | \ge 3 $。我们继续分析:要么B中没有没有顶点对是G的边,则 $ \alpha(G) \ge 3 $,否则存在顶点 $ x,y \in B $形成G的一条边。第二种情况集合 $ \{u, x, y \} $引入一个G的完全子图,且因此 $ \omega(G) \ge 3 $
注意我们需要区分多少情况来区分证明6个顶点图形的定理。在上面定理的证明中我们使用了一个特殊的情况,$ t = 2, n_ {1} = n_ {2} = 3 $,和如下著名的定理
定理(鸽笼定理)
设 $ n_ {1}, n_ {2}, \ldots, n_ {t} $为自然数,设X为至少 $ 1 + \sum^{t}_ {i=1} (n_ {i} - 1) $个元素的集合,且设 $ X_ {1}, X_ {2}, \ldots, X_ {t} $为不相交集合形成X的分区。则存在i使得 $ X_ {i} $有至少 $ n_ {i} $个元素
对图形的Ramsey定理
定理(对图形的Ramsey定理)
设图形G有至少 $ {k + \ell - 2 \choose k - 1} $个顶点,则 $ \omega(G) \ge k $ 或 $ \alpha(G) \ge \ell $
让我们记定理的条件对k和 $ \ell $是对称的,因为 $ {k + \ell + 2 \choose k - 1} = { k + \ell - 2 \choose \ell - 1} $
如果我们在定理中用 $ k = \ell = 3 $替代,我们获得每个有 $ {4 \choose 2} = 6 $个顶点的图形G满足 $ \omega(G) \ge 3 $ 或 $ \alpha(G) \ge 3 $
证明 我们继续在 $ k + \ell $上进行归纳。对 k = 1 或 $ \ell = 1 $容易看到该表述是满足的(对k = 2或 $ \ell = 2 $也是)
现在让我们假设 $ k, \ell \ge 2 $且表述对 $ k, \ell - 1 $和 $ k - 1, \ell $成立。我们把 $ n = {k + \ell - 2 \choose k - 1 }, n_ {1} = {k + \ell - 3 \choose k - 1} $和 $ n_ {2} = {k + \ell - 3 \choose k - 2} $。通过Pascal公式我们有 $ n = n_ {1} + n_ {2} $,且我们重写为形式 $ n = 1 + ((n_ {1} - 1) + (n_ {2} - 1) + 1) $,则通过鸽槽原理可得证
设G = (V, E)为有n个顶点的任意图形。我们想要显示 $ \omega(G) \ge k $或 $ \alpha(G) \ge \ell $。让我们选择任意一个顶点 $ u \in V $。我们根据顶点是否连接到u分割剩下的顶点为两个集合A和B,如下图:
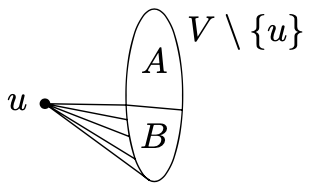
形式化为:
$ A = \{v \in V \ \{u \}: \{u, v\} \notin E \} $
$ B = \{v \in V \ \{u \}: \{u, v\} \in E \} $
通过鸽盒原理我们有 $ | A | \ge n_ {1} $ 或 $ | B | \ge n_ {2} $。如果 $ | A | \ge n_ {1} $,我们对$ (k, \ell - 1) $使用归纳假设。我们通过集合A满足$ \omega(G_ {A}) \ge k $或 $ \alpha(G_ {A}) \ge \ell - 1 $归纳得到图形 $ G_ {A} $。前一种情况我们有 $ \omega(G) \ge k $,后一种情况任意独立集合 $ I \subset A $与顶点u一起组成一个独立集合 $ I \cup \{u \} $,这样 $ \alpha(G) \ge \alpha(G_ {A}) + 1 \ge \ell $
在 $ | B | \ge n_ {2} $的情况下,我们继续分析且我们也能获得 $ \omega(G) \ge k $ 或 $ \alpha(G) \ge \ell $。这样归纳步骤结束
定理证明允许我们引入如下定义。设 $ r(k, \ell) $记为最小自然数使得有n个顶点的每个图形G满足 $ \omega(G) \ge k $或者 $ \alpha(G) \ge \ell $。数 $ r(k, \ell) $被称为ramsey数,Ramsey图形定理保证 $ r(k, \ell) $对每个 $ k \ge 1 $ 且 $ \ell \ge 1 $存在
让我们总结Ramsey数的值:
$ \begin{aligned} r(1, \ell) &= 1, \quad r(k, 1)=1 \\ r(2, \ell) &= \ell, \quad r(k, 2)=k \\ r(3,3) &=6 . \end{aligned} $
只有少数的一些Ramsey数已知。例如,r(4, 4) = 18,但r(5, 5)的值还未知
Ramsey数的一个更低的边界
本节我们引入Ramsey数的一个基本属性之一。我们显示数r(k, k),为简洁起见我们记为r(n),非常快的以指数增长。在形式化和证明结果之前,让我们回忆提供一个r(k)的下边界意味着什么:如果我们声称r(k) > n,我们断言n个顶点的某个图形G的存在,G满足 $ \omega(G) < k $且 $ \alpha(G) < k $。(特别地,检查 $ n < {2k - 2 \choose k - 1} $还不够,因为表达式 $ {2k - 2 \choose k - 1} $只是r(k)的一个上限,且k(k)可能更小)
例如,在之前的章节中使用图形 $ C_ {5} $我们证明了r(3) > 5。我们也提及没有证据证明r(4) = 18。不等式r(4) > 17可通过如下图证明:
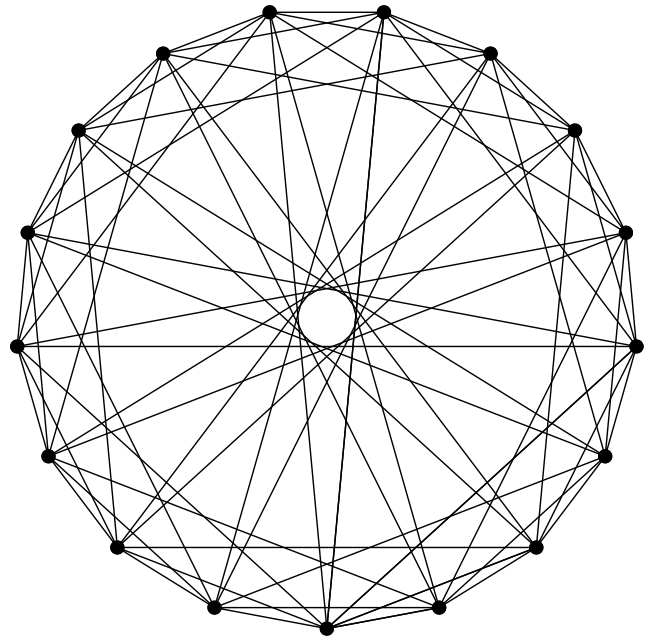
有趣地是,r(3) > 5和r(4) > 17对应的图形是同构的。这里我们将用概率的方法证明r(k)的下界
定理
设k和n为自然数满足 $ { n \choose k } \cdot 2^{1 - {k \choose 2}} < 1 $,则r(k) > n
什么样的k和n满足定理条件?通常在概率方法中,我们将使用非常粗略简单地估计:
$ {n \choose k} \le \frac{n^{k}}{k!} < \frac{n^{k}}{2^{k/ 2 + 1}} $
(该不等式只在 $ k \ge 3 $时成立)。我们根据定理有
$ {n \choose k} \cdot 2^{1 - {k \choose 2}} < \frac{n^{k}}{2^{k / 2 + 1}} \cdot 2^{1 - k(k-1)/2} = (\frac{n}{2^{k / 2}})^{k} $
这样定理的条件对 $ n = 2^{k / 2} $时满足
引理
对所有 $ k \ge 3 $我们有 $ r(k) > 2^{k / 2} $
该不等式对k = 2也有效
定理证明 我们考虑一个随机图形G,其顶点集合为 $ V = \{1, \ldots, n \} $,每个可能的 $ {n \choose 2 } $条边以 $ \frac{1}{2} $概率出现,跟其他边独立
设K为V中一个任意的k元素子集。设 $ A_ {K} $记为事件“K的顶点组成一个G的完整子图“。$ A_ {K} $的概率 $ P(A_ {K}) $为$ 2^{-{k \choose 2}} $。相似地,如果我们记 $ B_ {K} $为事件“K的顶点组成G的一个独立集合“,则 $ P(B_ {K}) = 2^{-{k \choose 2}} $ 。$ C_ {K} = A_ {K} \cup B_ {K} $(例如,K组成一个完全子图或一个独立集合)的概率为 $ 2 \cdot 2^{- {k \choose 2}} = 2^{1 - {k \choose 2}} $。设p记为概率,存在一个k元素 $ K \subseteq V $,使得 $ C_ {K} $发送。该概率很难确定,因为事件 $ C_ {K} $一般不独立。但对我们的目的它有效估计了p,通过把所有 $ C_ {K} $的概率加和:
$ p \le \sum_ {K \subseteq V, | K | = k} P(C_ {K}) $
我们然后获得 $ p \le {n \choose k} \cdot 2^{1 - {k \choose 2}} $,且因此,定理的假设确保 p < 1。但这意味着V中存在至少一个图形其 $ \alpha, \omega $都小于k
我们注意到证明不提供任意方法来构建想要的图形印证 $ r(k) > 2^{\frac{k}{2}} $。不止这个证明不提供方法:现在还没有这样的图形构建被发现