Table of Contents
统计证明
命题
存在一个n个变量的布尔函数不能被任意少于 $ 2^{n} / \log_ {2}{(n+8)} $个符号的公式定义。例如,对23个变量我们需要超过一百万个符号的公式
证明 所有n个变量的布尔函数的数量是 $ 2^{2^{n}} $,其n个变量公式的数量被最多m个符号写出的不超过 $ (n + 8)^{m} $个,因为公式中每m个位置可被n + 7个可能的符号填充,或可能是空白。这样,我们也统计了许多无意义的字符串符号,但一个初略的上限是有的。如果 $ 2^{2^{n}} > (n + 8)^{m} $,则存在一个布尔函数不能被最多m个符号表达。通过算法中的不等式,我们获得 $ m \ge 2^{n} / \log_ {2}{(n+8)} $
问题
假设 $ \mathcal{M} $的每个集合都是k个元素。则 $ \mathcal{M} $系统中不能两颜色着色的最小的个数m(k)是多少?
容看得到m(2) = 3,因为我们需要3条边来使图形不能两分。但对k = 3时问题要复杂很多。在之前的章节中,我们有一个7个3元组的系统不是两着色的,名为Fano plane,这样m(3) <= 7。事实上,m(3) = 7;为证明这个,我们需要显示所有6个或更少的3元组系统是可以两着色的。我们开始一个一般化陈述来给定一个k = 3的弱化边界。然后,对某些更大的效应,我们将改进k = 3的特殊情况的结果
定理
我们有 $ m(k) \ge 2^{k-1} $,例如,任意大小为k的系统集合元素个数小于 $ 2^{k-1} $是一个两着色的
证明 设 $ \mathcal{M} $为某个集合X的k元素子集的系统,且设 $ | \mathcal{M} | = m $。我们通过如下随机过程给X的每个点着上红色或白色。对每个点 $ x \in X $,我们投一个硬币。如果我们得到头面我们把x着上白色否则我们着上红色
设 $ M \in \mathcal{M} $为考虑的系统中k元组之一。M中所有点在随机着色中获得相同颜色的概率是什么?所有k个点同时为白色的概率是 $ 2^{-k} $,且所有点同时为红色的概率为 $ 2^{-k} $。M不是同为一个颜色的概率为 $ 2 \cdot 2^{-k} = 2^{1-k} $。因此 $ \mathcal{M} $中m个集合至少一个是单色的概率是 $ m2^{1-k} $。如果该数字严格小于1,例如,如果 $ m < 2^{k-1} $,则我们随机着色是两着色对系统 $ \mathcal{M} $是一个非零的概率。因此,至少一个两着色存在
对很大的k,函数m(k)增长$ 2^{k} $(更精确地,我们有 $ m(k) = \Theta(2^{k}k^{1/3}) $且 $ m(k) = O(2^{k}k^{2}) $;)且这样定理给出一个非常好的主意,另一方面,对k = 3我们只给出估计 $ m(k) \ge 4 $,我们使用两个技巧改进该边界
定理 $ m(3) \ge 7 $
我们必须显示一个有限集合X上任意6个元组的系统是可两着色的。我们区分两种情况:$ | X | \le 6 $和 $ | X | > 6 $。只有前一种情况需要用概率讨论
引理 设X为一个集合最多6个元素,且设 $ \mathcal{M} $为X上最多6个元组的系统。则 $ \mathcal{M} $是可两着色的
证明 如果需要,我们添加更多的点到X使得它有6个点。我们随机选择6个点中的3个着上白色,其他3个着上红色。如果M是 $ \mathcal{M} $中任意一个元组,则只有两种可能让M为单色:要么M全红剩下的3个点为白色,或M全白其他点为红色。因此M是单色的概率是 $ \frac{1}{10} $。$ \mathcal{M} $中的6个元组中的一些变成单色的概率不超过 $ \frac{6}{10} < 1 $,因此有一个两着色存在
相同的证明也显示6个点上的任意9个元组也是两着色的
对第二步骤,我们需要如下定义。设 $ (X, \mathcal{M}) $为一个集合系统,设x, y为X中两个元素。我们说x和y是连通的如果存在一个集合 $ M \in \mathcal{M} $包含x和y。如果x和y为不连通的点,我们定义一个新的集合系统 $ (X^{\prime}, \mathcal{M}^{\prime} $通过粘合x和y到一起。点x和y被一个z点替代,我们把z放入之前包含x或y的所有集合中。形式化为:$ X^{\prime} = (X \ \{x, y\}) \cup \{z\}, M^{\prime} = \{ M \in \mathcal{M}: M \cap \{x, y\} = \emptyset\} \cup \{(M \ \{x, y\}) \cup \{z\}: M \in \mathcal{M}, M \cap \{x, y\} \ne \emptyset \} $
让我们记如果点x和y不连通且 $ \mathcal{M} $是一个3元组的系统,则 $ (X^{\prime}, M^{\prime}) $也是一个三元组系统,且集合 $ X^{\prime} $比X少一个点。进一步我们声称如果 $ (X^{\prime}, \mathcal{M}^{\prime}) $是两着色的则 $ (X, \mathcal{M}) $也是一个两着色的。考虑一个两着色的集合 $ X^{\prime} $,及对应的集合X,x和y为z的颜色,容易看到不会出现单色集合。因此,为完成定理证明,提供以下引理:
引理 设 $ (X, \mathcal{M}) $为 $ | X | \ge 7 $的6个元组的系统,则X包含两个点在 $ \mathcal{M} $中不连通
证明 一个三元组 $ M \in \mathcal{M} $使得3对点连接。因此6个三元组使得最多 $ 3 \cdot 6 = 18 $个点对连接。但点对的总数目在7元素集合中为 $ \left(\begin{array}{l} 7 \\ 2\end{array}\right) = 21 $,因此一些点对没有连接(至少3个)
让我们标记m(4)未知(对更大的k也是)。它容易得出m(4)可通过有限多个配置(4元组系统)计算出。但配置的数量超出所有超级计算机的能力
有限概率空间
定理(Turan’s theorem)
对任意n个顶点的图形G,我们有
$ \alpha(G) \ge \frac{n^{2}}{2 | E(G) | + n} $
$ \alpha(G) $记为图形G中顶点最大独立集合的大小,一个独立集合是一个顶点集合使得其相互不会被一条边连接
该概率方法用来证明如下引理:
引理 对任意图形G,我们有
$ \alpha(G) \ge \sum_ {v \in V(G)} \frac{1}{\operatorname{deg}_ {G}(v) + 1} $
( $ \operatorname{deg}_ {G}(v) $记为图形G中顶点v的度数)
证明 假设G的顶点为 $ 1, 2, \ldots, n $,让我们用一个随机的顶点排列 $ \pi $。我们定义一个集合 $ M = M(\pi) \subseteq V(G) $,包含所有顶点v使得v的所有邻居u满足 $ \pi(u) > \pi(v) $;即顶点v在 $ \pi $的排序中在所有它的邻居前面。注意集合 $ M(\pi) $在G中是一个独立集合,且对任意排列 $ \pi $有 $ | M(\pi) | \le \alpha(G) $。因此 $ E[|M|] \le \alpha(G) $。我们现在用不同的方法计算M的期望大小
对一个顶点v,设 $ A_ {v} $为事件 $ v \in M(\pi) $。如果 $ N_ {v} $记为顶点v的所有邻居的集合,则集合 $ N_ {v} \cup \{v\} $的所有顺序在排序 $ \pi $下有相同的概率,且这样v为该集合最小元素的概率为 $ 1 / (| N_ {v} | + 1) = 1 / (\operatorname{deg}_ {G}(v) + 1) $。因此 $ P(A_ {v}) = 1 / (\operatorname{deg}_ {G}(v) + 1) $,且我们可计算:
$ \begin{aligned} \alpha(G) &\ge E[|M|] = \sum_ {v \in V(G)}E[I_ {A_ {v}}] \\ &= \sum_ {v \in V(G)}P(A_ {v}) = \sum_ {v \in V(G)}P(A_ {v}) = \sum_ {v \in V(G)}\frac{1}{\operatorname{deg}_ {G}(v) + 1} \end{aligned} $
定理的证明 边 $ e = | E(G) | $的数量是顶点度数的一半。这样我们有如下情形:对非负实数 $ d_ {1}, d_ {2}, \ldots, d_ {n} $,我们知道 $ \sum_ {i=1}^{n} d_ {i} = 2e $,且我们问和的最小可能值是
$ \sum_ {i=1}^{n} \frac{1}{d_ {i} + 1} $
它可显示和最小时是 $ d_ {1} = d_ {2} = \cdots = d_ {n} = 2e / n $。这样,该值即为定理中的值 $ n^{2} / (2e + n) $
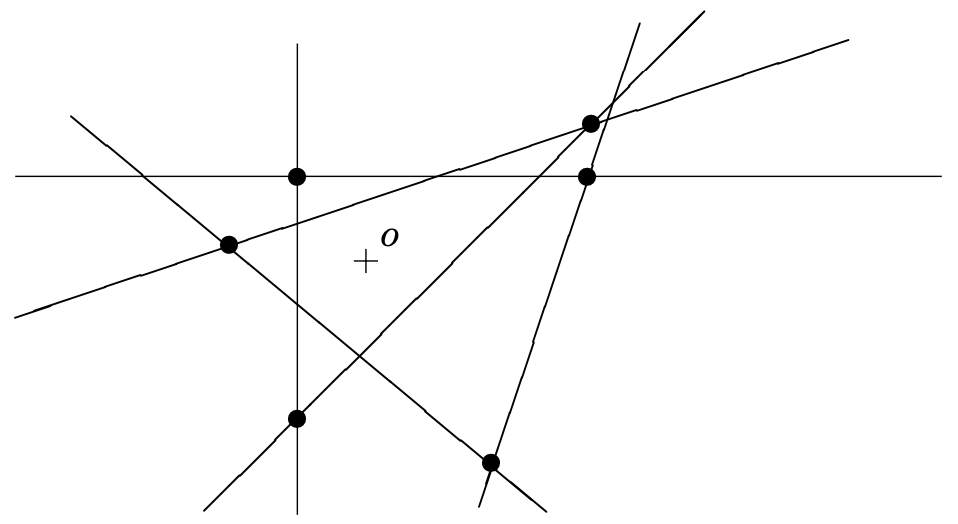
$ \le k $的交的数量 这是某些几何算法分析中的一个几何问题。让我们考虑一个集合L包含平面中n条线,使得没有3条线会有公共点且相互不会平行。设o为一个不在L中的点。我们将考虑L中的线相交对。每对线有一个交点,因此一共有 $ {n \choose 2} $个相交。我们说如果线段ov相交则一个相交v有k个,两条线定义一个交v,L至少有k条线。对给定的n和k,交最多为k的最大可能相交数为多少?以下定理给定一个上界,其为常量比例的最大可能值
定理 对n条线的任意集合,对最多交为k的情况下存在最多3(k + 1)n个交
证明 首先我们看特殊的情况k = 0。我们发现为0的交为凸多边形的顶点包含点o。因为每条线贡献最多多边形的一条边,则边的数量最多为n,且因此交的数量在交为0的情况下最多为n。我们将对任意k使用这个证明
设p记为某个适合的数字在区间(0, 1)中,该值将在证明的最后确定。让我们想象如下随机实验。我们随机选择一个子集 $ R \subseteq L $,通过以概率p选择每条线 $ \ell \in L $,这些选择对线 $ \ell $的分布独立
让我们回到我们的几何情形。我们有已选择的一个随机集合 $ R \subseteq L $的线。我们定义一个随机变量 f = f(R)作为交的数量其交水平为0;即R的线的交使得没有R的线模糊点o的视线。我们用两种办法估计期望E[f]。通过在证明的开始标签,我们有 $ f(R) \le | R | $对任意特殊集合R,且因此 $ E[f] \le E[|R |] $。容易计算 $ E[| R |] = pn $
现在我们用另一种办法统计E[f]。对L的线的每个交v,我们定义一个事件 $ A_ {v} $发生当且仅当v是R的线的水平为0的交的一个,例如,它贡献1到f(R)的值。事件A发生当且仅当如下两个条件满足:
- 两条线决定R上的交v
- 没有线交线段ov于一个内部点(这样会模糊点v到点o的视线)
我们推断 $ P(A_ {v}) = p^{2}(1 - p)^{\ell (v)}, \ell (v) $记为交v的水平
设M记为L的线的所有交的集合,且设 $ M_ {k} \subseteq M $为交的水平最多为k的集合。我们有
$ \begin{aligned} E[f] &= \sum_ {v \in M}E[I_ {A_ {v}} ] = \sum_ {v \in M}P( A_ {v}) \ge \sum_ {v \in M_ {k}}P(A_ {v}) \\ &= \sum_ {v \in M_ {k}}p^{2}(1 - p)^{\ell (v)} \ge \sum_ {v \in M_ {k}}p^{2}(1 - p)^{k} = | M_ {k} |p^{2}(1 - p)^{k} \end{aligned} $
这样我们导出了 $ np \ge E[f] \ge | M_ {k} | p^{2}(1-p)^{k} $,即
$ | M_ {k} | \le \frac{n}{p(1-p)^{k}} $
让我们这样选择p使得右边的值尽可能小。一个合适的选择,例如,p = 1 / (k + 1),通过之前的练习题,我们有对任意 $ k \ge 1, (1 - \frac{1}{k+1})^{k} \ge e^{-1} > \frac{1}{3} $,这使得 $ | M_ {k} | \le 3(k + 1)n $,如定理声明
定理
设 $ x_ {1} < x_ {2} < \cdots < x_ {n} $为增序的实数序列。设 $ \pi $为集合 $ \{1, 2, \ldots, n \} $的一个排序,且设 $ T(\pi) $为快速排序算法对输入序列 $ (x_ {\pi(1)}, x_ {\pi(2)}, \ldots, x_ {\pi(n)}) $所做的比较的数量,则 $ T(\pi) $对一个随机排序 $ \pi $的期望最多为 $ 2n \ln{n} $
让我们标记任意算法排序每个n元组不同的实数和只使用配对比较在最坏的情况下至上要做 $ \log_ {2}{n!} $次比较。因为算法根据比较的输出必须选择 $ n! $种可能的排序中的一个,且k次比较只有 $ 2^{k} $也不同的输出。根据我们之前做过的习题,我们有 $ n! \ge (\frac{n}{e})^{n} $,这样 $ \log_ {2}{n!} = (\log_ {2}{e})\ln {n!} \ge (\log_ {2}{e})(n - 1) \ln{n} \approx 1.443(n-1) \ln{n} $。因此,快速排序平均行为被定理保证