Table of Contents
定义和基本属性
finite projective plane是带某些属性的有限集合的子集的系统
定义
设X为一个有限集,且设 $ \mathcal{L} $为X的子集的系统。二元组 $ (X, \mathcal{L}) $被称为finite projective plane,如果它满足如下公理:
(P0) 存在一个4元素集合 $ F \subseteq X $使得对每个集合 $ L \in \mathcal{L}, | L \cap F | \le 2 $
(P1) 任意两个不同的集合 $ L_ {1}, L_ {2} \in \mathcal{L} $ 相交只有一个元素,例如,$ | L_ {1} \cap L_ {2} | = 1 $
(P2) 对任意两个不同的元素 $ x_ {1}, x_ {2} \in X $,只存在一个集合 $ L \in \mathcal{L} $ 使得 $ x_ {1} \in L, x_ {2} \in L $
如果 $ (X, \mathcal{L}) $是一个finite projective plane,我们X的元素为点,$ \mathcal{L} $的集合为线。如果 $ x \in X $是一个点而 $ L \in \mathcal{L} $是一条线,我们说“点x在线L上“或“线L穿过点x“
如果我们用这种新语言表达公里(P0) - (P2),他们开始跟几何陈述相似。公里(P1)说任意两个不同的线只相交于一个点,公理(P2)告诉我们只有一条线穿过两个不同的点。公理(P0)需要4个点存在使得没有3个点共线
如果 $ a, b \in X $为finite projective plane上两个不同的点,包含a和b的唯一的线 $ L \in \mathcal{L} $被记为符号 $ \bar{ab} $。如果 $ L, L^{\prime} \in \mathcal{L} $为不同的线,$ L_ {1} \cap L_ {2} $的唯一点被称为它们的交
我们依然还欠读者一个projective plane中projective的解释。首先,我们应该显示什么是projective转换。考虑两个3维欧几里得空间中的平面 $ \rho $ 和 $ \sigma $和一个不在这两个平面中的点c,且从点c映射 $ \rho $中的每个点到平面 $ \sigma $。这定义了一个映射,称为从 $ \rho $到 $ \sigma $的projective转换。如果 $ x \in \rho $是一个点使得线段cx平行于平面 $ \sigma $,则在欧几里得几何中,x的像是未定义的。但如果我们补充 $ \rho $和 $ \sigma $一个无穷远的线使得它们变成projective planes,则这个projective转换是这两个projective planes间的双射。如果 $ \rho $和 $ \sigma $被考虑为同一平面的拷贝,我们认为这个映射是projective plane到其自身的双射。projective plane是一个适当的域可做projective几何,一个考虑projective几何适当的域和保留projective转换的配置的几何分支。例如,projective转换映射conic部分(圆、椭圆、抛物线和双曲线)到conic部分,但一个椭圆可被转换为一个双曲线,等,且一个conic部分的伟大统一理论可在projective几何中建立
实际projective plane的finite projective plane的相似用来作为各种记号的动机,且通常也为目的(我们可绘制几何图像)。在真实projective plane上的几何考虑和使用公理(P0) - (P2)只运用在finite projective planes上。不要忘记一个finite projective plane只是一个带(P0) - (P2)属性的有限集合系统,因此其他几何记号不能自动转换到它身上。例如,在finite projective plane上没有距离,因此它没有圆的明确定义。另一个重要的不同是在通常的几何平面上,每条线的点可被该线自然排序,但在finite projective plane上没有这样的排序
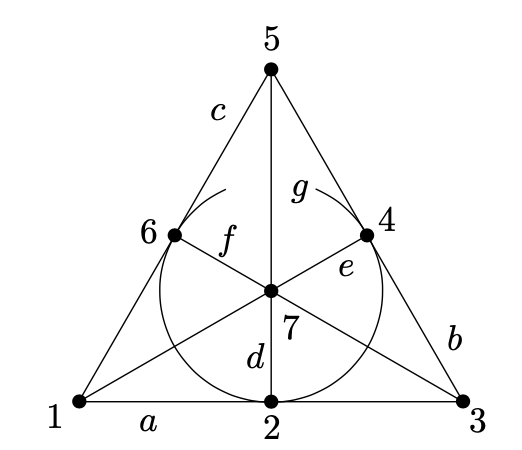
例子 一个有限projective plane最小可能的例子是7个点和7条线,每条线有3个点,且它称为Fano plane。如上图。这些点被标记为1-7,且每条线上的3个点被一个线段连接,这些连接线被标签为a-g
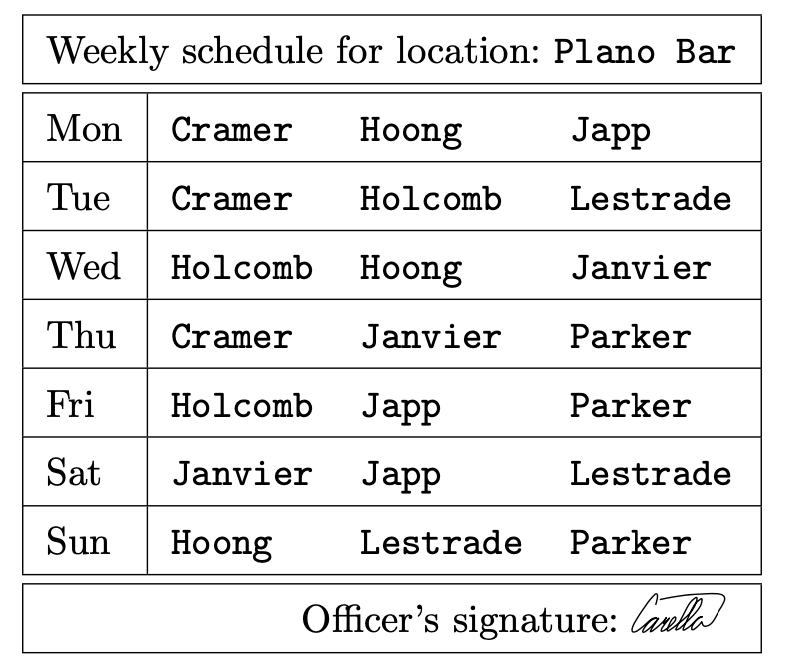
Fano plane虽然小,但是一个有用的数学对象,且它也作为各种谜题或一些高级问题的解决方案出现,比如如下这个。7个警察被转换到第87区域的各个区,一个好的时机是让他们互相观察在西南C Drive的Plano Bar,这里是一个简单甚至乏味地值班因为酒吧的顾客通常是计算机罪犯,数字钱币伪造者或类似的人。需要一个3人移动小组,一周1天服务。如何安排每周调度使得7人中的每两人会值班一周?Fano plane提供了好的解决方案(点对应警察,移动对应线,以某种顺序排列)。每个人有相同编号的移动,没有人会超过连续两天,但另一方面,每个移动有一个人在前一天也在并知道发生了什么。我们不知道这样的调度在实际中会被警方使用,但例如,一些摩托循环赛会根据基于affine plane的order four来组织
命题 设 $ (X, \mathcal{L}) $为一个finite projective plane。则所有它的线有相同数量的点;即 $ \forall L, L^{\prime} \in \mathcal{L}, | L | = | L^{\prime} | $
证明 任意选择两条线 $ L, L^{\prime} \in \mathcal{L} $,首先我们证明一个辅助声明:存在一个点 $ z \in X $不在 $ L, L^{\prime} $上
证明辅助声明。选择一个集合 $ F \subseteq X $作为公理(P0),我们有 $ | L \cap F | \le 2 $且 $ | L^{\prime} \cap F | \le 2 $。如果F不在 $ L \cup L^{\prime} $中则得证。唯一剩下的可能性是L交F于两点(称为a,b)且 $ L^{\prime} $交F于两点(记为c,d)。则我们考虑线 $ L_ {1} = \overline{ac} $和 $ L_ {2} = \overline{bd} $,设z为 $ L_ {1} $和 $ L_ {2} $的交点
如下几何图形显示了该情形:
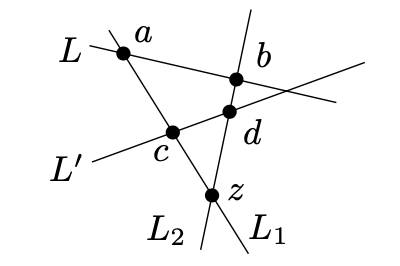
当然,我们不得不非常小心只使用(P0) - (P2),而不是图形中的额外信息。在许多方面,finite projective plane跟几何(欧几里得)平面很不同
我们断言 $ z \notin L \cup L^{\prime} $。线L和 $ L_ {1} $交于一点,名为a,且这样如果 $ z \in L $,我们得到z = a。但这是不可能的因为线 $ L_ {2} $会包含点z = a, b和d,F中的3个点。这被条件P0禁止。因此 $ z \notin L $,且相似地我们可得到 $ z \notin L^{\prime} $。这完成了辅助声明的证明
现在我们显示线L和 $ L^{\prime} $有相同的大小。我们定义一个映射 $ \varphi: L \to L^{\prime} $;它是一个双射。我们固定一个点 $ z \notin L \cup L^{\prime} $且定义点 $ x \in L $的象 $ \varphi(x) $作为线 $ \overline{zx} $和 $ L^{\prime} $的交,如下图所示:
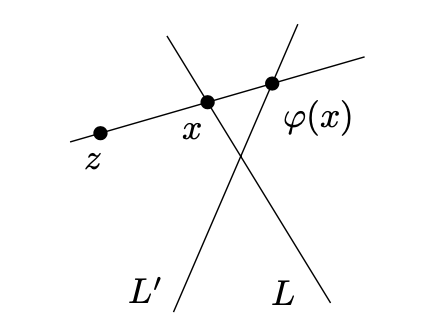
通过公理(P1)和(P2),点 $ \varphi(x) $是定义的。接着,我们检查 $ \varphi $是双射。如果 $ y \in L^{\prime} $是一个任意点,我们考虑线 $ \bar{zy} $,且设x为和线L的交点,则线 $ \bar{zy} $和 $ \bar{zx} $共线,因此我们有 $ y = \varphi(x) $,则映射 $ \varphi $是一个双射且 $ | L | = | L^{\prime} | $
定义(projective plane的序) finite projective plane $ (X, \mathcal{L}) $的序是 $ | L | - 1 $。$ L \in \mathcal{L} $是一条线(根据证明过的命题,序不依赖线的选择)
例如,Fano plane有序2(线有三个点),且它是唯一的序为2的projective plane
命题 设$ (X, \mathcal{L}) $为一个序为n的projective plane,则我们有
(i) 只有n + 1条线穿过X中的每个点
(ii) $ | X | = n^{2} + n + 1 $
(iii) $ | \mathcal{L} | = n^{2} + n + 1 $
证明(i) 考虑一个任意点 $ x \in X $。首先我们观察到存在一条线不包含x。即如果F是4点配置如(P0),且 $ a,b,c \in F $为不同于x的点,则至少线 $ \overline{ab} $ 和 $ \overline{ac} $有一条线不包含x
固定这样的一条线L,$ x \notin L $。对每个点 $ y \in L $,我们考虑线 $ \overline{xy} $;有n + 1条线通过x点。另一方面,任意包含x的线交L在某点 $ y \in L $且因此它有n + 1条线穿过x
证明(ii) 我们选择某条线 $ L = \{ x_ {0}, x_ {1}, x_ {2}, \ldots, x_ {n} \} \in \mathcal{L} $且一个点 $ a \notin L $,如下图所示:
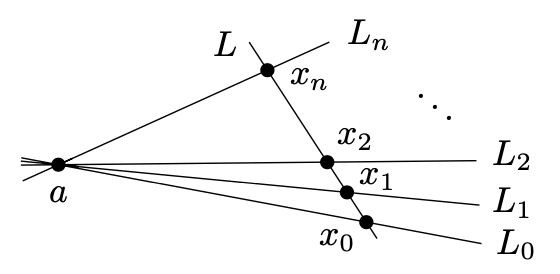
设 $ L_ {i} $记为线 $ \overline{a x_ {i}}, i = 0, 1, \ldots, n $。根据(P1),任意两条线,$ L_ {i} $和 $ L_ {j} $,交于一个点,为点a。线 $ L_ {0}, L_ {1}, \ldots, L_ {n} $每个除了a还有n个点,且因此它们一共包含 $ (n + 1)n + 1 = n^{2} + n + 1 $个不同的点。它也显示对任意点 $ x \in X \ \{a\} $位于某条线 $ L_ {i} $上。通过(P1),线 $ \overline{ax} $交线于点 $ x_ {i} $,且通过(P2),线 $ \overline{ax} $必须和L相交。这证明了(ii)
我们现在忽略(iii)的证明。在续集中,我们将学习一个重要的原理,且从它我们看到(iii)立马得到证明
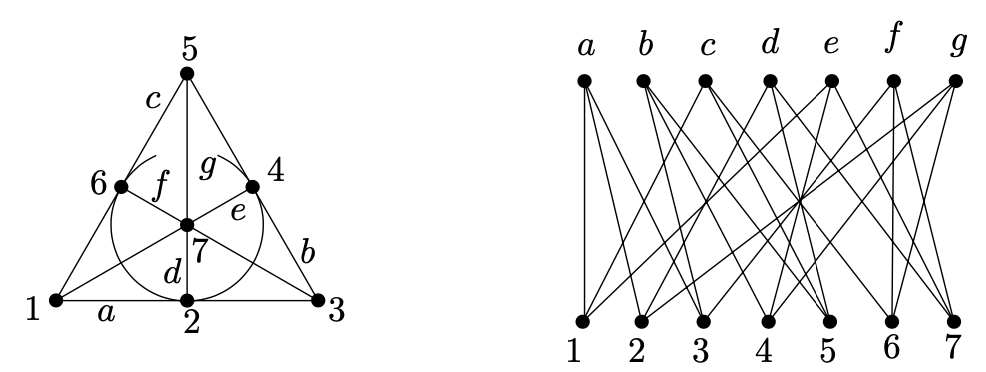
Duality duality的意思在projective planes中是“交换点和线的角色“。为了精确地公式化,我们先引入finite projective plane的发生图形。事实上,发生图形可被一个集合X的子集的任意系统 $ \mathcal{S} $定义。发生图形是一个顶点集合 $ X \cup \mathcal{S} $的二分图,每个集合 $ S \in \mathcal{S} $被一条边连接到所有点 $ x \in S $。结果每个点 $ x \in X $连接到包含它的所有集合。简单地说,我们可说发生图形的每条边对应成员关系 $ \in $。Fano plane的发生图形如上图;点被对应点和线的标签标签(结果的图形是漂亮且重要的图形,虽然在我们的绘制中比较丑陋,它甚至有个名字:the Heawood graph)
给定一个finite projective plane $ (X, \mathcal{L}), (X, \mathcal{L}) $的dual通过$ (X, \mathcal{L}) $的发生图形获得且解释为线是点的顶点,顶点为点的集合。在上图中,我们可上下翻转该图形。因为 $ \mathcal{L} $现在被认为是一个点集,对 $ \forall x \in X $,线的集合 $ \{ L \in \mathcal{L}: x \in L \} $被解释为一条线。在上图例子中,dual的点为 $ \{a, b, \ldots, g\} $,dual的线为 $ \{a, c, e \} $(对Fano plane中点1),$ \{a, d, g\} $(对点2),等等
命题 finite projective plane的dual也是一个finite projective plane
证明 设 $ (X, \mathcal{L}) $为一个finite projective plane。$ (X, \mathcal{L}) $的dual是一对 $ (\mathcal{L}, \Lambda), \Lambda $是一个 $ \mathcal{L} $子集的系统,每个子集对应X中的某个点(注意不同的点为 $ \mathcal{L} $不同的子集,因为两个点只共享一条线)
我们需要验证 $ (\mathcal{L}, \Lambda) $的条件(P0) - (P2)。我们以P0开始。如果这个条件转换为原始集合系统 $ (X, \mathcal{L}) $的语言,它意味着我们需要找到4条线 $ L_ {1}, L_ {2}, L_ {3}, L_ {4} \in \mathcal{L} $使得不会有3条线共一个点。让我们考虑一个4点配置 $ F = \{a, b, c, d\} \subseteq X $作为条件(P0),且定义 $ L_ {1} = \overline{ab}, L_ {2} = \overline{cd}, L_ {3} = \overline{ad}, L_ {4} = \overline{bc} $。如果我们看这4条线的任意3条,任意两条共享F中的一个点,且该点不包含在第3条上。因此$ L_ {1}, \ldots, L_ {4} $中的任意3条线只有空的交集,这样我们确认了dual集合系统的条件(P0)的验证
dual $ (\mathcal{L}, \Lambda) $的条件(P1)需要:如果 $ x, x^{\prime} \in X $为两个不同点,则存在只有一条线 $ L \in \mathcal{L} $包含x和 $ x^{\prime} $。这就是$ (X, \mathcal{L}) $需要的条件(P2),我们发现dual的(P2)是原始projective plane $ (X, \mathcal{L}) $的(P1)的结果
现在我们称finite projective plane的dual为dual projective plane。dual projective plane有和projective plane相同的序
一般地,如果我们有关于序为n的finite projective plane的一些有效的陈述,且如果我们交换点和线,我们也能获得一个有效地陈述。例如,如果原始陈述说“线 $ L_ {1}, L_ {2} $交于点x“,我们可在dual中说“点 $ x_ {1}, x_ {2} $被线L连接“
finite projective planes的存在
序2、3、4和5的projective planes存在。但不存在序为6的projective planes。序为7、8、9的projective planes存在,但序为10的不存在。这有一般化规律吗?它得出一个序为n的projective plane存在当一个n个元素的域存在。这里一个域是代数上的概念;即它是一个带加法、减法、乘法和除法满足某个公理 - 如果你不熟悉定义看附录。代数教给我们,一个n元素的域存在当且仅当n是一个素数的次方
对一个可被至少两个不同的素数整除的n,没有n个元素的域存在,但不知道是否有一个序为n的projective plane存在。有一些部分负的结果;例如,如果数n被4整除余1或2且它不能为两个整数平方的和则没有序为n的projective plane存在。这使得我们不用考虑序6、14和许多其他的projective planes的存在,但它不能覆盖所有的可能性。例如,它不能处理序10或12
序为10的projective plane存在已经被排除。这里有一个有趣的历史。对序6,Euler给出了一个证明尝试,但只有Tarry在1900年给出了一个令人信服的论证。对序10,最近被使用大量的计算机计算给出了一个证明。对更高的序12,projective plane的存在仍然是一个开放式的问题。明显这个问题可通过检查有限数量的配置来解决,但对当代的计算技术来说配置的数量来起来太过巨大
一个projective plane的代数结构 对有兴趣且缺乏代数背景的读者,我们解释如何从域构建一个projective plane。我们特别对finite projective planes感兴趣,但构建对实数的projective plane也起作用
直接看上去比较复杂,因为结果的projective plane的点相当于有序三元组的集合。然而,一旦给定定义,检查projective plane的公理是很直接的。在例子中域是R,实数,构建有直观地几何解释,我们将在最后呈现。对有些人来说几何解释会帮助形式化构建,但对另一些人可能导致更加混乱,所以这取决于读者的品味,多少抽象应该放入几何直观
构建用某些域K开始。对实数的projective plane(例如,使用欧几里得平面通过无穷远点做适当的扩展),我们使用所有实数域R作为K。如果我们选择K的n个元素域,构建结果为一个序n的finite projective plane。我们运行的例子是K的3元素域,例如,集合 $ \{0, 1, 2\} $及模3操作
首先我们考虑集合 $ T = K^{3} \backslash \{(0, 0, 0) \} $;即集合的所有有序三元组(x,y,t),$ x, y, t \in K $且x, y, t不同时为0。在这样的T中,我们定义一个相等关系 $ \approx $如下:$ (x_ {1}, y_ {1}, t_ {1} ) \approx (x_ {2}, y_ {2}, t_ {2}) $当且仅当一个非零的 $ \lambda \in K $存在使得 $ x_ {2} = \lambda x_ {1}, y_ {2} = \lambda y_ {1}, t_ {2} = \lambda t_ {1} $。构建的projective plane的点用这种相等关系分类。porjective plane这样产生通常被记为 $ PK^{2} $,例如,实数的projective plane通常被记为 $ PR^{2} $
为了获得projective plane一个更好的直观,我们从每个相等 $ \approx $类中选择一个代表性的三元组。对这些代表,我们选择三元组其最后一个非零部分为1。因此,代表为(x, y, 1),(x, 1, 0)和(1, 0, 0)的三元组。容易得出任意其他的三元组跟上述形式的一个三元组相等
总是说相等类有些麻烦,这样我们说一个点(x, y,t)在续集中,表示整个相等类包含(x, y, t)
如果K是一个n元素域,我们现在可统计我们获得多少个点。形如(x, y, 1)的点的个数为 $ n^{2} $个,形如(x, 1, 0)的点有n个,形如(1, 0, 0)的点只有一个 - 总共 $ n^{2} + n + 1 $个。对n = 3,这些标签的所有点绘制如下图表:
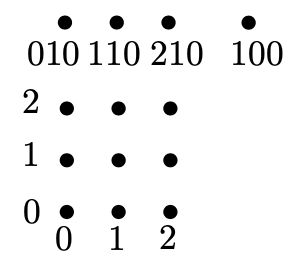
现在我们定义线,对 $ \forall (a, b, c) \in K^{3} \ \{(0, 0, 0)\} $,我们定义一条线L(a,b,c)作为所有满足如下等式的projective plane点(x, y, t)的集合:
$ ax + by + ct = 0 $
明显,两个相等的点(x,y,t)和$ (\lambda x, \lambda y, \lambda t) $要么都满足该等式要么都不满足,且因此我们有定义projective plane点的某个集合。对 $ \forall \lambda \in K, \lambda \ne 0 $,三元组 $ (\lambda a, \lambda b, \lambda c) $定义和三元组(a, b, c)相同的线。因此,三元组上定义线我们有相同的相等关系。我们可选择相同的代表三元组,例如,最后一个非零元素为1的。如下图,我们已绘制所有的线通过点(0, 0, 1)。我们已忽略多数点的标签:
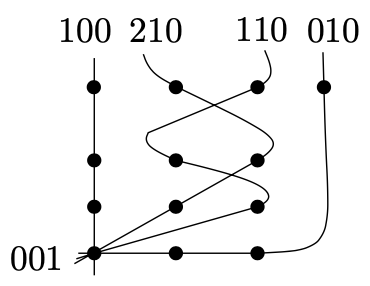
为了显示一个n元素域,我们已构建了一个序为n的finite projective plane,我们必须检查条件(P0) - (P2)。我们以条件P1开始,设 $ (a_ {1}, b_ {1}, c_ {1}) $和 $ (a_ {2}, b_ {2}, c_ {2}) $为两个不等的三元组,例如,一个不是另一个的倍数
我们可直接计算两条线的交点。让我们考虑三元组作为域K上的3维向量,我们容易得到其线性无关,因此,矩阵
$ \left( \begin{array}{ccc} a_ {1} & b_ {1} & c_ {1} \\ a_ {2} & b_ {2} & c_ {2} \end{array} \right) $
有rank 2。且存在3个数 $ x, y, t \in K $,它们不能同时为0,使得
$ x(a_ {1}, a_ {2}) + y(b_ {1}, b_ {2}) + t(c_ {1}, c_ {2}) = (0, 0) $
这样点(x, y, t)是两条线的交点
另一方面,因为矩阵的rank是2,两个线性无关的列存在。假设,例如,为 $ (a_ {1}, a_ {2}), (b_ {1}, b_ {2}) $。这意味着对任意向量(u, v),等式 $ x(a_ {1}, a_ {2}) + y(b_ {1}, b_ {2}) = (u, v) $有唯一的解。即两条线交于同一点
条件P2可相似地得到证明,P0的证明留给读者
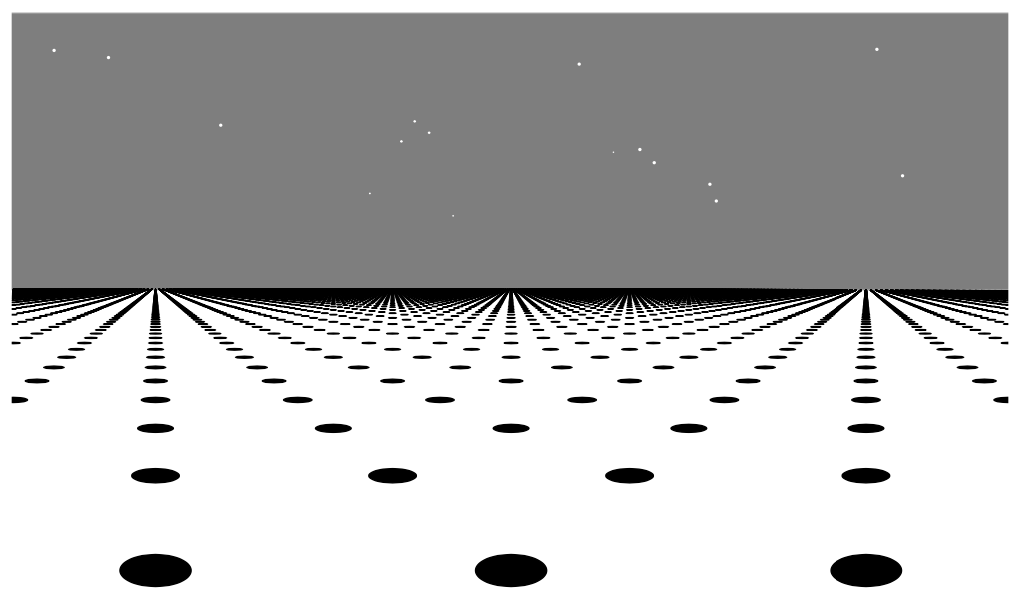
几何解释 如我们在本章开头提到的,构建实数projective plane的基本思想是通过无穷远点扩展欧几里得平面,这样对欧几里得平面中线的每个方向有一个对应的无穷远点,使得所有平行的线相交。如上图
为了使这类图像更形式化,我们考虑Cartesian坐标系统(x, y, t),t轴是垂直的,这样的3维空间。欧几里得平面放置在这个3维空间中作为水平平面,t = 1,如下图灰色部分:
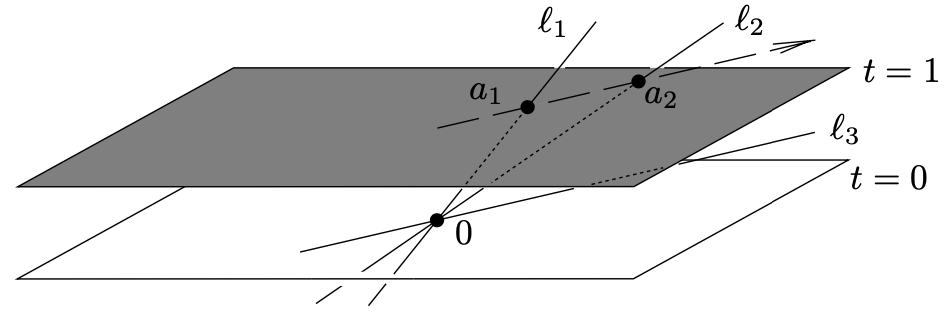
平面的每个点a对应一条线 $ \mathcal{l} = \overline{0a} $经过3维空间的源点。例如,点 $ a_ {1} $在上图中对应线 $ \mathcal{l}_ {1} $。相反地,经过3维空间源点的每条线对应灰色平面的一个点,除了水平线,比如$ \mathcal{l}_ {3} $
我们注意到当我们开始倾斜线 $ \mathcal{l}_ {1} $到 $ \mathcal{l}_ {2} $的位置,然后再到水平线 $ \mathcal{l}_ {3} $,对应的灰色平面的点沿着一条线的轨迹回退到无穷远。这样就不自然地想到水平线比如 $ \mathcal{l}_ {3} $对应到无穷远点。这里我们使用一个典型地现代数学的技巧 - 不去解释无穷远点对应水平线,我们忘掉原始的欧几里得平面,说projective plane的点为三维空间经过源点的线。我们没有描述 $ PK^{2} $的形式化构建,但projective plane的点是形如 $ \{(\lambda x, \lambda y, \lambda t): \lambda \in K \ \{ 0 \} \} $的集合,其几何上来说是$ K^{3} $上经过源点的一条线
projective plane的线对应经过源点的三维空间的平面
上述构建可能给出projective plane一些点的映像,那些无穷远点,是比较特殊的,和其他点不同。但并不是这样,没有点有特殊性,且无穷远在某些程度上只是为了方便
垂直Latin方块
一个序为n的Latin方块是一个n行n列的方块表。每个条目是集合 $ \{1, 2, \ldots, n \} $中的数,集合中每个数在每行每列中只出现一次。两个3 x 3的Latin方块描述如下:
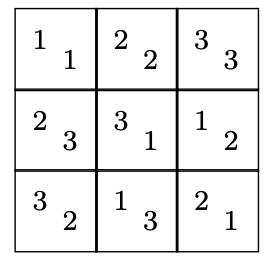
现在我们说相同序的两个Latin方块是垂直的是什么意思。想象其中一个方块是透明的,我们让它盖在另一个方块上,如上图
这样,我们获得 $ n^{2} $个有序对,每对由透明方块的一个条目和盖在其下的另一个方块的条目构成。考虑方块是垂直的如果没有重复的有序对
定理 设M为序为n的Latin方块集合,使得每两个都是垂直的。则 $ | M | \le n - 1 $
证明 我们开始如下观察。设A和B为序为n的垂直Latin方块,设 $ \pi $为数字 $ 1, 2, \ldots, n $的某些排列。让我们做一个新的Latin方块 $ A^{\prime} $,其位置(i, j)上的条目为数字 $ \pi(a_ {ij}) $,$ a_ {ij} $是方块A在位置(i, j)上的条目。通过垂直的定义,不难看到 $ A^{\prime} $和B也是垂直Latin方块。该观察可被语法“Latin方块的垂直性不被其一重命名符号而改变“
为证明定理,想象我们有Latin方块 $ A_ {1}, A_ {2}, \ldots, A_ {t} $,每两个都是垂直的。对每个 $ A_ {i} $,用这样的方法排列符号(例如,数字 $ 1, 2, \ldots, n $),结果Latin方块 $ A^{\prime}_ {i} $的第一行为 $ (1, 2, \ldots, n ) $。通过上述的观察,Latin方块 $ A^{\prime}_ {1}, \ldots, A^{\prime}_ {t} $仍然是相互垂直的。让我们看在方块 $ A^{\prime}_ {i} $的位置(2, 1)上会占据什么数字。首先,这个条目不可能为1,因为第1行第1列已经是1。进一步,没有两个方块 $ A^{\prime}_ {i} $和$ A^{\prime}_ {j} $在位置(2, 1)上有相同的数字;如果有,通过 $ A^{\prime}_ {i} $盖住 $ A^{\prime}_ {j} $,我们可得到一对确定的数字,为(k, k)在位置(2,1)上,但该对已出现在首行第k列条目上。因此数字 $ 2,3, \ldots, n $每个只能出现在某个$ A^{\prime}_ {i} $上的位置(2,1)上一次,因此 $ t \le n - 1 $
定理
对任意n > 2,一个序为n的projective plane存在当且仅当存在一个有n - 1个序为n的相互垂直的Latin方块的收集
证明 我们将不描述细节。只是描述如何从Latin方块构建一个projective plane及相反。给定n - 1个序为n的垂直Latin方块 $ S_ {1}, \ldots, S_ {n-1} $,我们将产生一个序为n的projective plane
首先我们定义构建平面的点集X。它在无穷远有n + 1个点,记为r, c和 $ s_ {1}, s_ {2}, \ldots, s_ {n-1} $和$ n^{2} $个点(i, j),$ i, j = 1, 2, \ldots, n $。接下来,我们用几个步骤引入线。一条线 $ B = \{r, c, s_ {1}, \ldots, s_ {n-1} \} $包含无穷远点。则我们有n条线 $ R_ {1}, R_ {2}, \ldots, R_ {n} $,使得
$ R_ {i} = \{ r, (i, 1), (i, 2), \ldots, (i, n) \} $
且n条线
$ C_ {j} = \{c, (1,j), (2, j), \ldots, (n, j)\} $
它们所有绘制如下图(n = 3):
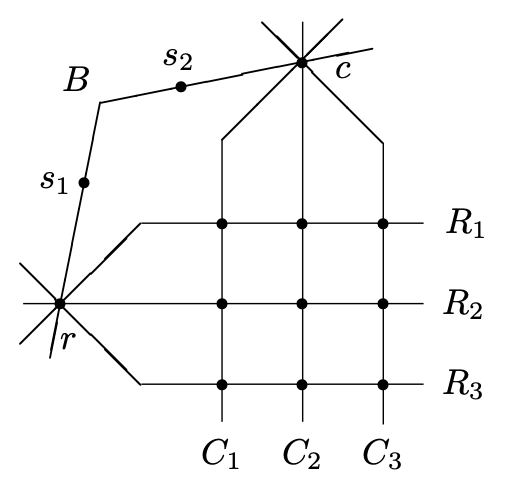
绘制的点和线及标签跟序为n的任意projective plane相同。现在方块指定projective plane的线穿过点 $ s_ {1}, s_ {2}, \ldots, s_ {n-1} $(除了线B)。作为被选中的记号建议,Latin方块 $ S_ {k} $确定线穿过点 $ s_ {k} $。如果 $ (S_ {k})_ {ij} $记为 $ S_ {k} $在i行j列的条目,我们定义线:
$ L_ {km} = \{ s_ {k} \} \cup \{(i, j): (S_ {k})_ {ij} = m \} $
$ m = 1, 2, \ldots, n, k = 1, 2, \ldots, n- 1$。例如,如果 $ S_ {1} $是上上图左边的Latin方块,则线 $ L_ {11} $对应方块的数字1有 $ L_ {11} = \{ s_ {1}, (1, 1), (2, 3), (3, 2)\} $
这完成了有限的projective plane对应n - 1个垂直的Latin方块的收集的描述。它仍然验证了projective plane的公理。它容易计算线和点的总数量是 $ n^{2} + n + 1 $
为证明定理相等,我们还要显示从序n的projective plane中构建n - 1个垂直的Latin方块。该构建跟上述构建相反方向相似。在projective plane中,我们任意选择两个不同的点r和c,且我们固定如以上构建中的记号。则第k个Latin方块 $ S_ {k} $根据线穿过点 $ s_ {k} $填充
组合应用程序
在组合数学中,finite projective planes常常作为各种不寻常属性的集合系统的例子。可以说如果我们有一些有限集合系统的假设且寻找它的一个反例,或如果我们想要一个带某种描述属性的集合系统的例子,则它可能是一个好想法尝试在第一个替代者之间的一个有限projective planes
我们尝试在数学中文档化projective planes的用处
用两种颜色着色集合系统 设X为一个有限集合,设 $ \mathcal{M} $为X的子集的系统。我们说集合系统 $ \mathcal{M} $是两着色的如果它可能用两种给定的颜色之一着色X中的每个点,设为红或白,使得每个集合 $ M \in \mathcal{M} $包含两种颜色的点(两着色能力通常被称为属性B)
例如,如果 $ X = \{1,2,3\} $且 $ \mathcal{M} = \{\{1,2\}, \{1,3\}, \{2,3\} \} $则 $ \mathcal{M} $不是两着色的。更一般地,如果 $ \mathcal{M} $中所有集合只有两个颜色,则我们可记 $ (X, \mathcal{M}) $为一个图,且这里两着色意味着图形两分。如果 $ \mathcal{M} $的集合每个超过2个点呢?例如,如果 $ \mathcal{M} $中所有集合都是3个点?它证明是两着色能力的情形比图形更复杂。例如,是否一个给定的 $ \mathcal{M} $是可两着色的问题是算法上困难的
让我们考虑如下自然的问题:一个包含3个点的集合的集合系统 $ \mathcal{M} $不是可两着色的最小集合数是什么?它的答案为7,且Fano plane提供了答案的一半:它有7个包含3个点的集合,且它是唯一有7个集合的集合系统不能两着色的!我们将处理答案的另一半,例如,显示所有的系统带6个或更少集合是可两着色的方法
我们可讨论更多关于两着色能力的问题,它在组合中非常重要,但这里我们只想指出该领域的一些问题,用projective plane能处理的
更多关于无 $ k_ {2,2} $及很多边的图形 之前的定理告诉我们如果G是一个m个点的图形,且没有 $ K_ {2,2} $的子图形,则G有最多 $ \frac{1}{2} (m^{3/2} + m) $条边。使用finite projective plane,我们显示该边界接近一般化上最好的可能
定理
对m的无穷多个值,存在一个m个点的无 $ K_ {2,2} $的图形有至少 $ 0.35 m^{3/2} $条边
证明 使用一个序为n的projective plane,考虑它的发生图形。该图形的点的数量是 $ m = 2(n^{2} + n + 1) $。$ n^{2} + n + 1 $的每条线有n + 1个点,这意味着边的总数是 $ (n^{2} + n + 1)(n+ 1) \ge (n^{2} + n + 1)^{3/2} = (\frac{m}{2})^{3/2} \approx 0.35m^{3/2} $
如果发生图形包含一个 $ K_ {2,2} $的子图形意味着什么?在projective plane的语言中,为存在两个点 $ x, x^{\prime} $和两条线 $ L, L^{\prime} $使得 $ x \in L, x^{\prime} \in L, x \in L^{\prime}, x^{\prime} \in L^{\prime} $。这在projective plane中不可能发生
常量0.35还可以改进,优化值为0.5