Table of Contents
微分法
微分方法
定理 连续性是微分可能性的必要条件
但是它不是充分条件
例子,$ f(x) = x \sin{\frac{1}{x}}, f(0) = 0 $的f(x)在0时的区间上连续,x = 0时却不能微分。实际上
$ \frac{f(h) - f(0)}{h} = \sin{\frac{1}{h}} $
当 $ h \to 0 $时,极限不存在
上述函数在x = 0这一点是特异点,Weierstras(1872)作出了区间各点都不能微分的连续函数的例子时,震惊了当时的数学界
复合函数的微分
定理 f(x) $ \varphi(t) $微分存在,则 $ F(t) = f(\varphi(t)) $微分存在
$ F^{\prime} (t) = f^{\prime}(x) \cdot \varphi^{\prime}(t) $
即
$ \frac{dy}{dt} = \frac{dy}{dx} \cdot \frac{dx}{dt} $
这是复合函数的微分法
证明 t的变动为 $ \Delta t $,x的变动为 $ \Delta x $,这样y的变动为 $ \Delta y $
$ \frac{\Delta y }{\Delta t} = \frac{\Delta y}{\Delta x} \cdot \frac{\Delta x}{\Delta t} $
当 $ \Delta t \to 0 $时
$ \frac{\Delta x}{\Delta t} \to \frac{dx}{dt} $
同时当 $ \Delta x \to 0 $时
$ \frac{\Delta y}{\Delta x} \to \frac{dy}{dx} $
所以
$ \frac{\Delta y}{\Delta t} \to \frac{dy}{dx} \cdot \frac{dx}{dt} $
这样
$ F^{\prime}(t) = f^{\prime}(x)\varphi^{\prime}(t) $
注意上述证明方法的问题
x为独立变量,$ \Delta x $任意的话需要 $ \Delta x \ne 0 $,上面的情况是x是t的函数值,$ \Delta t $的值引起 $ \Delta x = 0$的情况是有的。这样的话,之前的证明写法有不合理的地方,变量 $ \Delta x, \Delta y $的写法要做修改如下:
$ \Delta y = f^{\prime}(x) \Delta x + \epsilon \Delta x, \quad \Delta x = \varphi^{\prime}(t)\Delta t + \epsilon^{\prime} \Delta t $
当 $ \Delta t \to 0 $时, $ \epsilon^{\prime} \to 0 $,有 $ \Delta x \to 0 $,但 $ \Delta t \ne 0 $时,$ \Delta x = 0 $的情况也有。$ \Delta x = 0 $时 $ \epsilon = 0 $定义为 $ \Delta t \to 0 $时 $ \epsilon \to 0 $,这样
$ \begin{aligned} \Delta t &= (f^{\prime}(x) + \epsilon)(\varphi^{\prime}(t) + \epsilon^{\prime}) \Delta t \\ &= f^{\prime}(x)\varphi^{\prime}(t) \cdot \Delta t + [\epsilon \varphi^{\prime}(t) + \epsilon^{\prime} f^{\prime}(x) + \epsilon \epsilon^{\prime}] \Delta t \end{aligned} $
右边括弧中的用 $ \epsilon^{\prime \prime} $表达,则
$ \Delta y = f^{\prime}(x) \varphi^{\prime}(t) \Delta t + \epsilon^{\prime \prime} \Delta t, \quad \epsilon^{\prime \prime} = \epsilon \varphi^{\prime}(t) + \epsilon^{\prime} f^{\prime}(x) + \epsilon \epsilon^{\prime} $
当 $ \Delta t \to 0 $时 $ \epsilon^{\prime \prime} \to 0 $,则
$ dy = f^{\prime}(x) \varphi^{\prime}(t) dt $
这样结果为
$ dy = f^{\prime}(x)dx $
同样,y为x的函数,x为t的函数,t为u的函数时,微分为
$ \frac{dy}{du} = \frac{dy}{dx} \frac{dx}{dt} \frac{dt}{du} $
逆函数的微分法
假设有一个 $ a \le x \le b $区间上的连续函数y = f(x)。如果y在该区间的最大值和最小值为p和q,则y可取遍 $ p \le y \le q $区间上的任意值。但是,只有当y = f(x)是单调的,才能通过x值唯一确定一个y值
如果f(x)不是单调的,$ x_ {1} < x_ {2} < x_ {3} $对应 $ y_ {1} < y_ {2} < y_ {3} $及$ y_ {1} > y_ {2} > y_ {3} $都有可能。如果 $ y_ {1} < y_ {2}, y_ {2} > y_ {3}, y_ {2} \eta > Max(y_ {1}, y_ {3}) $,区间 $ (x_ {1}, x_ {2}) $及 $ (x_ {2}, x_ {3}), \eta = f(x) $的x的值最少会出现一次
单调的时候,区间 $ p \le y \le q $中y=f(x)中各种值唯一对应。对应 $ x = \varphi(y), \varphi $是f的逆函数。这样,f是 $ \varphi $的逆函数,f和 $ \varphi $互为逆函数
定理18 关于x的区间的函数y单调且连续,则y的变动区间中x是其反函数。反函数也连续单调。如果y可微则x也可微
$ \frac{dy}{dx} \cdot \frac{dy}{dx} = 1 $
证明:我们用y = f(x), $ x = \varphi(y) $表示两个函数。$ x = \xi $对应 $ y = \eta $。$ \{y_ {n}\} $为收敛到 $ \eta $的任意单调数列,对应 $ \{x_ {n} \} $单调有界,极限值收敛到 $ \lambda $。由于f(x)的连续性,$ f(\lambda) = \eta $,则有 $ \lambda = \varphi(\eta) = \xi $。则 $ y_ {n} \to \eta $的同时 $ x_ {n} \to \xi $,即 $ \varphi(y_ {n}) \to \varphi(\eta) $,这样反函数 $ \varphi(y) $连续
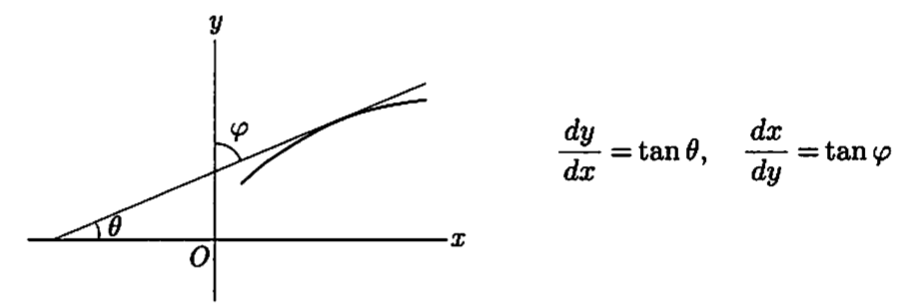
有
$ \frac{\Delta x}{\Delta y} = 1 / \frac{\Delta y}{\Delta x} $
当 $ \Delta y \to 0 $时,有$ \Delta x \to 0 $,同时 $ \lim{\frac{\Delta x}{\Delta y}} = 1 / \lim{\frac{\Delta y}{\Delta x}} $,即 $ \frac{d x}{d y} = 1 / \frac{d y}{d x} $
但 $ \frac{d y}{d x} = 0 $的情况要排除
取三角函数的逆函数的例子
(1) $ \arcsin{x} $
y = sinx 在区间 $ - \frac{\pi}{2} \le x \le \frac{\pi}{2} $,一般化区间为
$ (2n - 1)\frac{\pi}{2} \le x \le (2n + 1)\frac{\pi}{2}, \qquad (n = 0, \pm 1, \pm 2, \cdots) $
内单调,y在区间 $ -1 \le y \le 1 $之间取值。则函数y = sinx的逆函数,即 $ x = \arcsin{y} $中y在 $ -1 \le y \le 1 $之间,所以x必须限定为上述区间中的一个
这样从y = sinx中有
$ \frac{d \sin{x}}{d x} = \cos{x}, \qquad \frac{d \arcsin{y}}{d y} = \frac{1}{\cos{x}} = \pm \frac{1}{\sqrt{1 - y^{2}}} $
由于我们选取 $ - \frac{\pi}{2} \le x \le \frac{\pi}{2} $区间,则 $ \cos{x} \ge 0 $。则这里 $ \pm $应该为 +,这样变量x,y置换可得
$ d \arcsin{x} = \frac{1}{\sqrt{1 - x^{2}}} $
(2) $ \arctan{x} $
$ y = \tan{x} $在区间 $ - \frac{\pi}{2} < x < \frac{\pi}{2} $内从 $ -\infty $ 到 $ + \infty $单调递增。这样arctan定义为
$ y = \arctan{x}, \qquad - \frac{\pi}{2} < y < \frac{\pi}{2} $
例如:
$ \arctan{0} = 0, \qquad \arctan{\pm 1} = \pm \frac{\pi}{4} \\ \arctan{\pm \infty} = \lim_ {x \to \pm \infty} \arctan{x} = \pm \frac{\pi}{2} $
从 $ y = \tan{x}, \frac{dy}{dx} = \frac{1}{\cos^{2}{x}} = 1 + y^{2} $,通过记号变换,有
$ \operatorname{D}{\arctan{x}} = \frac{1}{1 + x^{2}} $
例1,$ y = \arcsin{\sqrt{1 - x^{2}}} $意味着 $ \sqrt{1 - x^{2}} = \sin{y} $。从而 $ x^{2} = \cos^{2}{y}, x = \pm \cos{y} $。$ \arcsin $的主值在ABC如下图,y的主值微分为
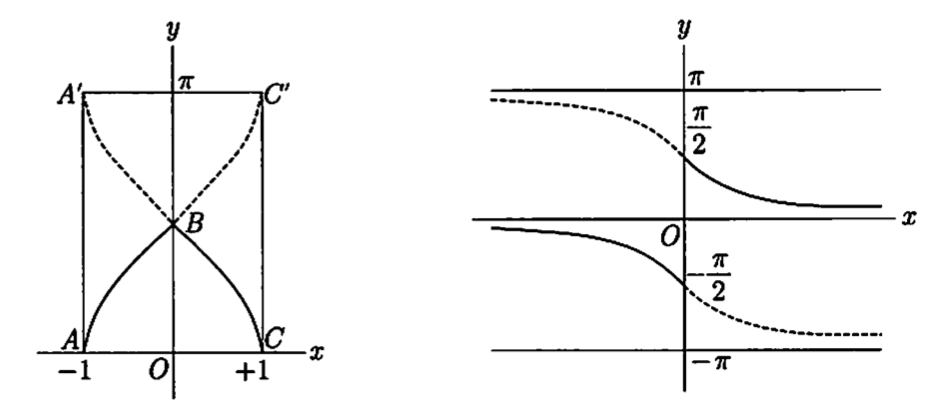
$ \frac{dy}{dx} = \frac{1}{\sqrt{1 - (1 - x^{2})}} \frac{-x}{\sqrt{1 - x^{2}}} = \frac{1}{| x |} \frac{-x}{\sqrt{1 - x^{2}}} = \mp \frac{1}{\sqrt{1 - x^{2}}} \qquad (x \ge 0) $
当x = 0时 $ \operatorname{D^{+}}{y} = -1, \operatorname{D^{-}}{y} = +1 $
指数函数和对数函数
当a > 0时,对 $ a^{x} $微分有
$ \frac{d(a^{x})}{dx} = \lim_ {h \to 0}{\frac{a^{x+h} - a^{x}}{h}} = a^{x} \lim_ {h \to 0}\frac{a^{h} - 1}{h} $
因为h > 0,则 $ a^{h} > 1 $,则设 $ a^{h} = 1 + \frac{1}{t}, t > 0 $。当 $ h \to 0, a^{h} \to 1, t \to \infty $
从 $ h = \log_ {a}{(1 + \frac{1}{t})} $中得到
$ \frac{a^{h} - 1}{h} = \frac{\frac{1}{t}}{\log_ {a}{(1 + \frac{1}{t})}} = \frac{1}{\log_ {a}{(1 + \frac{1}{t})^{t}}} $
当 $ h \to 0, t \to \infty $有 $ (1 + \frac{1}{t})^{t} \to e $,因为 $ \log_ {a} $是连续函数,$ h \to 0 $时 $ \log_ {a}{(1 + \frac{1}{t})^{t}} \to \log_ {a}{e} $。则
$ \lim_ {h \to 0}{\frac{a^{h} - 1}{h}} = \frac{1}{\log_ {a}{e}} = \log_ {e}{a} $
当h < 0时,把h用-h带入,得:
$ \frac{a^{-h} - 1}{-h} = \frac{a^{h} - 1}{h} \cdot \frac{1}{a^{h}}, \qquad (h > 0) $
当 $ h \to 0 $时, $ a^{h} \to 1 $,则有
$ \frac{a^{-h} - 1}{-h} \to \log_ {e}{a} $
所以
$ \frac{d(a^{x})}{dx} = a^{x} \log_ {e}{a} $
对数微分法 u, v, w为x的函数,u, v, w在x = 0时,$ \log{| uvw |} $微分为
$ \operatorname{D}\log{ | uvw | } = \operatorname{D}{(\log{| u |} + \log{| v |} + \log{| w |})} = \frac{u^{\prime}}{u} + \frac{v^{\prime}}{v} + \frac{w^{\prime}}{w} $
但是又
$ \operatorname{D}{\log{ | uvw | }} = \frac{(uvw)^{\prime}}{uvw} $
则
$ \frac{(uvw)^{\prime}}{uvw} = \frac{u^{\prime}}{u} + \frac{v^{\prime}}{v} + \frac{w^{\prime}}{w}, \qquad (u \ne 0, v \ne 0, w \ne 0) $
同样的
$ (\frac{u}{v})^{\prime} / \frac{u}{v} = \frac{u^{\prime}}{u} - \frac{v^{\prime}}{v} $
高阶微分法
y = f(x)的导数是 $ f^{\prime}(x) $,$ f^{\prime}(x) $的导数是 $ f^{\prime \prime}(x) $。第n阶导数是 $ f^{(n)}(x) $。$ f^{\prime \prime}(x) $可写为
$ \frac{d}{dx} (\frac{dy}{dx}) \text{ 或 } \frac{d^{2} y}{dx^{2}} $
同样的
$ \frac{d^{n}y}{dx^{n}} = f^{(n)}(x) $
上述记号中,$ dx^{2} $是 $ (dx)^{2} $,$ d^{2}y $是 $ d(dy) $,微分记号可写为
$ dy = y^{\prime}_ {x} dx $
两边微分,$ d(dy), d(dx) $表示 $ d^{2}y, d^{2} x $,得
$ d^{2}y = y^{\prime \prime}_ {x}(dx)^{2} + y^{\prime}_ {x}d^{2}x $
这里x为独立变量,$ dx = \delta x $,$ d^{2}x = d(\delta x) = 0 $,则
$ d^{2}y = y^{\prime \prime}_ {x}dx^{2} $
则 $ \frac{d^{2}y}{dx^{2}} = f^{\prime \prime}(x) $。而 $ x = \varphi(t) $,有 $ d^{2}x = x^{\prime \prime}_ {t}dt^{2} $,则
$ d^{2}y = y^{\prime \prime}_ {x}x^{\prime 2}_ {t} dt^{2} + y^{\prime}_ {x}x^{\prime \prime}_ {t}dt^{2} $
则有
$ \frac{d^{2}}{dt^{2}} f(\varphi(t)) = f^{\prime \prime}(\varphi(t)) \varphi^{\prime}(t)^{2} + f^{\prime}(\varphi(t))\varphi^{\prime \prime}(t) $
u, v为x的函数,则根据Leibniz法则有
$ \frac{d^{n}(uv)}{dx^{n}} = u^{(n)}v + {n \choose 1}u^{(n-1)}v^{\prime} + \cdots + {n \choose k}u^{(n-k)}v^{(k)} + \cdots + uv^{(n)} $
而 $ u / v $的高阶导函数没有简单的函数表示
偏微分
两个以上的变量,根据一个变量变动,相关的微分叫做偏微分。例如z = f(x, y)
$ \frac{\partial z}{\partial x} = \lim_ {\Delta x \to 0} \frac{f(x + \Delta x, y) - f(x,y)}{\Delta x}, \qquad \frac{\partial z}{\partial y} = \lim_ {\Delta y \to 0} \frac{f(x, y+\Delta y) - f(x, y)}{\Delta y} $
当区域内各点关于 $ \frac{\partial z}{\partial x}, \frac{\partial z}{\partial y} $存在时,这样的x, y函数
$ \frac{\partial z}{\partial x} = f_ {x}(x, y) = D_ {x} f(x, y), \quad \frac{\partial z}{\partial y} = f_ {y}(x, y) = D_ {y}f(x, y) $
同样对高阶微分
$ \frac{\partial}{\partial x} (\frac{\partial z}{\partial x}) = \frac{\partial^{2} z}{\partial x^{2}} = f_ {xx}(x, y) $
$ \frac{\partial}{\partial y} (\frac{\partial z}{\partial x}) = \frac{\partial^{2} z}{\partial x \partial y} = f_ {xy}(x, y), \quad \frac{\partial}{\partial x} (\frac{\partial z}{\partial y}) = \frac{\partial^{2} z}{\partial y \partial x} = f_ {yx}(x, y) $
$ \frac{\partial}{\partial y} (\frac{\partial z}{\partial y}) = \frac{\partial^{2} z}{\partial y^{2}} = f_ {yy}(x, y) $
三个以上的变量也一样
例1 $ \sqrt{x^{2} + y^{2}} = r $
$ f(x, y) = \log{r} = \frac{1}{2} \log{x^{2} + y^{2}} $
然而
$ f_ {x} = \frac{x}{x^{2} + y^{2}} = \frac{x}{r^{2}}, \qquad f_ {y} = \frac{y}{r^{2}} $
$ f_ {xx} = \frac{1}{x^{2} + y^{2}} - \frac{2x^{2}}{(x^{2}+y^{2})^{2}} = \frac{1}{r^{2}} - \frac{2x^{2}}{r^{4}} $
$ f_ {xy} = - \frac{2xy}{(x^{2} + y^{2})^{2}} = - \frac{2xy}{r^{4}} = f_ {yx} $
$ f_ {yy} = \frac{1}{r^{2}} - \frac{2y^{2}}{r^{4}} $
$ \frac{\partial^{2}f}{\partial x^{2}} + \frac{\partial^{2} f}{\partial y^{2}} $用 $ \Delta f $表示,则
$ \Delta f = \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2} f}{\partial y^{2}} = \frac{2}{r^{2}} - \frac{2(x^{2} + y^{2})}{r^{4}} = 0 $
例2 $ \sqrt{x^{2} + y^{2} + z^{2}} = r, f(x, y, z) = \frac{1}{r} = (x^{2} + y^{2} + z^{2})^{- \frac{1}{2}} $
$ f_ {x} = - \frac{x}{(x^{2} + y^{2} + z^{2})^{\frac{3}{2}}} = - \frac{x}{r^{3}}, \qquad f_ {y} = - \frac{y}{r^{3}}, \qquad f_ {z} = - \frac{z}{r^{3}} $
$ f_ {xx} = - \frac{1}{r^{3}} - x\{-3 \frac{1}{r^{4}} \cdot \frac{\partial r}{\partial x} \} = - \frac{1}{r^{3}} + \frac{3x}{r^{4}} \cdot \frac{x}{r} = - \frac{1}{r^{3}} + \frac{3x^{2}}{r^{5}} $
$ f_ {yy} = - \frac{1}{r^{3}} + \frac{3y^{2}}{r^{5}} $
$ f_ {zz} = - \frac{1}{r^{3}} + \frac{3z^{2}}{r^{5}} $
$ \Delta f = \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2} f}{\partial y^{2}} + \frac{\partial^{2} f}{\partial z^{2}} = - \frac{3}{r^{3}} + \frac{3(x^{2} + y^{2} + z^{2})}{r^{5}} = - \frac{3}{r^{3}} + \frac{3r^{2}}{r^{5}} = 0 $
$ f_ {xy} = -x(-3 \frac{1}{r^{4}} \cdot \frac{\partial r}{\partial y}) = 3 \frac{xy}{r^{5}} = f_ {yx} $
微分可能性 全微分
函数z = f(x, y)的一点P = (x, y)。$ \Delta z = f(x + \Delta x, y + \Delta y) - f(x, y) $,则
$ \Delta z = A \Delta x + B \Delta y + \varepsilon \rho $
A, B是跟 $ \Delta x, \Delta y $无关的系数,点(x, y)的值有的话,$ \rho $是定点(x,y)和动点 $ (x + \Delta x, y + \Delta y) $的距离 $ (\rho = \sqrt{(\Delta x)^{2} + (\Delta y)^{2}} ) $,$ \varepsilon $跟 $ \Delta x, \Delta y $相关,$ \rho \to 0 $时,$ \varepsilon \to 0 $。用之前页的记号有 $ \varepsilon \rho = o \rho $。这样函数z在点(x, y)微分是可能的
上面的等式成立的话,$ \Delta y = 0, \rho = | \Delta x | $时,
$ \frac{\Delta z}{\Delta x} = A \pm \varepsilon $
这时,$ \Delta x \to 0, \varepsilon \to 0 $的话,(x, y)的 $ \frac{\partial z}{\partial x} $存在,为A。同样的,$ \frac{\partial z}{\partial y} $存在,为B。点 $(x + \Delta x, y + \Delta y) $从点(x, y)一定方向上收敛时,$ \alpha $确定,$ \Delta x = \rho \cos{\alpha}, \Delta y = \rho \sin{\alpha} $时,
$ \frac{\Delta z}{\rho} = A \cos{\alpha} + B \sin{\alpha} + \varepsilon $
$ \lim_ {\rho \to 0} \frac{\Delta z}{\rho} = A \cos{\alpha} + B \sin{\alpha} = \frac{\partial z}{\partial x} \cos{\alpha} + \frac{\partial z}{\partial y} \sin{\alpha} $
这种情况下,$ \lim_ {\rho \to 0} \frac{\Delta z}{\rho} $是 $ \Delta x = \rho \cos{\alpha}, \Delta y = \rho \sin{\alpha} $方向上的偏微分商
之前的等式成立的话各方向上的偏微分商存在,即为上式
z可微分的话,$ \Delta z $的主要部分 $ \Delta x, \Delta y $的一次方程式 $ \frac{\partial z}{\partial x} \Delta x + \frac{\partial z}{\partial y} \Delta y $是z的全微分,用dz表示。特别地,z = x, z = y时 $ dx = \Delta x, dy = \Delta y $,这样全微分为
$ dz = \frac{\partial z}{\partial x} dx + \frac{\partial z}{\partial y} dy $
z可微分时 $ dz = \frac{\partial z}{\partial x} \Delta x + \frac{\partial z}{\partial y} \Delta y $为(x, y)关于曲面z = f(x, y)相接的平面。这样的平面上坐标为X, Y, Z的话,dx, dy, dz为 $ X - x, Y - y, Z - z $,接平面的方程式为
$ Z - z = \frac{\partial z}{\partial x}(X - x) + \frac{\partial z}{\partial y}(Y - y) $
这是接平面的定义
z = f(x, y)有领域的各点可微分时,这样的领域可微分。这样的情况下f(x, y)的领域是连续的
定理 $ \frac{\partial z}{\partial x}, \frac{\partial z}{\partial y} $领域存在且连续的时候,z的领域可微分
证明 $ \Delta x, \Delta y $用h, k带入得
$ \begin{aligned} \Delta z &= f(x + h, y + k) - f(x, y) \\ &= \{ f(x + h, y + k) - f(x, y + k)\} + \{ f(x, y + k) - f(x, y) \} \end{aligned} $
使用x的平均值定理
$ f(x + h, y + k) - f(x, y + k) = hf_ {x}(x + \theta h, y + k), \qquad 0 < \theta < 1 $
假设 $ f_ {x} $ 连续
$ f_ {x}(x + \theta h, y + k) = f_ {x}(x, y) + \varepsilon $
如果 $ h \to 0, k \to 0 $时 $ \varepsilon \to 0 $
y的偏微分
$ f(x, y + k) - f(x, y) = kf_ {y}(x, y) - \varepsilon^{\prime} k $
$ k \to 0 $时 $ \varepsilon^{\prime} \to 0 $,则
$ \Delta z = hf_ {x}(x, y) + k f_ {y}(x, y) + h \varepsilon + k \varepsilon^{\prime} $
$ | h | \le \rho, | k | \le \rho, (\rho = \sqrt{h^{2} + k^{2}}) $,所以 $ | h \varepsilon + k \varepsilon^{\prime} | \le (| \varepsilon | + | \varepsilon^{\prime} |) \rho $
$ \Delta z = hf_ {x}(x, y) + kf_ {y}(x, y) + o \rho $
即z是可微分的
注意 该定理的假设过大,上述证明用了 $ f_ {x} $的连续性。领域内 $ z_ {x}, z_ {y} $关于点(x, y)存在,这样如果连续的话,该点的z可微分
微分的顺序
f(x, y)关于x微分得导函数$ f_ {x}(x, y) $,$ f_ {x}(x, y) $关于y微分的导函数为 $ f_ {xy} $。这样 $ f_ {xy}, f_ {yx} $指代不同的事物。然而在一定条件下,$ f_ {xy}, f_ {yx} $为同一函数。现在采用这些条件中最容易获得的条件:
定理 在某个区域 $ f_ {xy}, f_ {yx} $连续的话这样的区域 $ f_ {xy} = f_ {yx} $
证明 对区域的任意一点(a, b)的附近考察
$ \Delta = f(a + h, b + k) - f(a + h, b) - f(a, b + k) + f(a, b) $
用图的记号有
$ \Delta = f(P_ {3}) - f(P_ {1}) - f(P_ {2}) + f(P) $
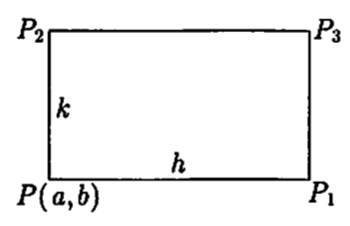
写成
$ \varphi(x) = f(x, b + k) - f(x, b) $
$ \varphi(a) = f(P_ {2}) - f(P), \varphi(a + h) = f(P_ {3}) - f(P_ {1}) $
$ \Delta = \varphi(a + h) - \varphi(a) $
假设(a, b)附近 $ f_ {x} $存在,则
$ \varphi^{\prime}(x) = f_ {x}(x, b + k) - f_ {x}(x, b) $
这样x = a 和 x = a + h之间,用 $ \varphi(x) $的平均值定理
$ \varphi(a + h) - \varphi(a) = h\varphi^{\prime}(a + \theta h) \qquad (0 < \theta < 1) $
综合得
$ \Delta = h\{ f_ {x}(a + \theta h, b + k) - f_ {x}(a + \theta h, b) \} $
假设(a, b)附近 $ f_ {xy} $存在,则右边y = b和y = b + k间,用平均值定理得
$ \Delta = hkf_ {xy}(a + \theta h, b + \theta^{\prime} k) \qquad (0 < \theta^{\prime} < 1) $
假设 $ f_ {xy} $在(a, b)点连续,则
$ \lim_ {(h, k) \to (0, 0)} \frac{\Delta}{hk} = f_ {xy}(a, b) $
x,h和y,k交换可得
$ \lim_ {h, k) \to (0, 0)} \frac{\Delta}{hk} = f_ {yx}(a, b) $
这样,区域内各点有
$ f_ {xy} = f_ {yx} $
在 $ f_ {x}, f_ {y}, f_ {xy} $存在的区域,该区域内一点 $ f_ {xy} $连续,这样的点 $ f_ {yx} $存在,且 $ f_ {xy} = f_ {yx} $(Schwarz定理)
如果区域内 $ f_ {x}, f_ {y} $存在,区域内某点可微,则在该点 $ f_ {xy} = f_ {yx} $(Young定理)
这里可用之前的式子证明,假定h = k且 $ f_ {x} $可微
$ f_ {x}(a + \theta h, b + h) = f_ {x}(a, b) + \theta h f_ {xy}(a, b) + h f_ {xy}(a, b) + oh $
$ f_ {x}(a + \theta h, b) = f_ {x}(a, b) + \theta h f_ {xx}(a, b) + oh $
这样 $ \Delta = h^{2} f_ {xy}(a, b) + oh^{2} $,有
$ \lim_ {h \to 0} \frac{\Delta}{h^{2}} = f_ {xy}(a, b) $
假设x, y对称,有$ f_ {xy}(a, b) = f_ {yx}(a, b) $
不能无条件的认为 $ f_ {xy} = f_ {yx} $,这个很重要,现在举一个例子
$ \left\{ \begin{array}{ll} f(x,y) = xy \frac{x^{2} - y^{2}}{x^{2} + y^{2}}, & (x, y) \ne (0, 0), \\ f(0, 0) = 0 \end{array} \right. $
$ (x, y) \ne (0, 0) $时计算得
$ f_ {x}(x, y) = \frac{3x^{2} - y^{3}}{x^{2} + y^{2}} - \frac{2x^{2}y(x^{2} - y^{2})}{(x^{2} + y^{2}x)^{2}} $
x,y 交换得 $ f_ {y} $,然而
$ f_ {xy}(x, y) = \frac{x^{2} - y^{2}}{x^{2} + y^{2}} + \frac{8x^{2}y^{2}(x^{2} - y^{2})}{(x^{2} + y^{2})^{3}} $
$ (x, y) \ne (0, 0) $时连续,$ f_ {yx} $相等,然而,$ f_ {xy}(0, y)= -1, (y \ne 0), \lim_ {y \to 0} f_ {xy}(0, y) = -1 $。然而,$ f_ {x}(0, y) = -y, y \ne 0 $,$ f_ {x}(0, 0) = 0 $时$ f_ {x}(0, y) $在y = 0时连续,这样 $ f_ {xy}(0, 0) = -1 $。同样的,$ f_ {yx}(x, 0) = 1 $时 $ f_ {yx}(0, 0) = 1 $
三阶以上,导函数连续的话,可以改变微分顺序。例如 $ f_ {xxy} = (f_ {x})_ {xy} = (f_ {x})_ {yx} = f_ {xyx} $,相邻的顺序进行交换,这样
$ f_ {xyz} = f_ {xzy} = f_ {zxy} = f_ {zyx} = f_ {yzx} = f_ {yxz} $
$ f_ {xxyy} = f_ {xyxy} = f_ {xyyx} = f_ {yxxy} = f_ {yxyx} = f_ {yyxx} $
这样二阶导函数
$ f_ {x^{2}} = \frac{\partial^{2} f}{\partial x^{2}}, \qquad f_ {xy} = \frac{\partial^{2} f}{\partial x \partial y}, \qquad f_ {y^{2}} = \frac{\partial^{2} f}{\partial y^{2}} $
第n阶为
$ f_ {x^{r}y^{s}} = \frac{\partial^{n} f}{\partial x^{r} \partial y^{s}} \qquad \qquad (r + s = n, s = 0, 1, 2, \ldots, n) $
高阶的全微分
u = f(x, y)的第一阶全微分
$ du = \frac{\partial u}{\partial x}dx + \frac{\partial u}{\partial y}dy $
$ \frac{\partial u}{\partial x} $可微分,x, y关于du的全微分为 $ d^{2} u $
即x, y为独立变量(h = dx, k = dy)
$ \begin{aligned} d^{2}u = d(du) &= \frac{\partial}{\partial x}(\frac{\partial u}{\partial x} h + \frac{\partial u}{\partial y} k)h + \frac{\partial}{\partial y}(\frac{\partial u}{\partial x} h + \frac{\partial u}{\partial y}k)k \\ &= \frac{\partial^{2} u}{\partial x^{2}}h^{2} + 2 \frac{\partial^{2}u}{\partial x \partial y} hk + \frac{\partial^{2} u}{\partial y^{2}} k^{2} \\ &= \frac{\partial^{2} u}{\partial x^{2}}d x^{2} + 2 \frac{\partial^{2} u}{\partial x \partial y}dxdy + \frac{\partial^{2} u}{\partial y^{2}} dy^{2} \end{aligned} $
同样的
$ d^{3}u = \frac{\partial^{3} u}{\partial x^{3}} dx^{3} + 3 \frac{\partial^{3}u}{\partial x^{2} \partial y} dx^{2}dy + 3 \frac{\partial^{3} u}{\partial x \partial y^{2}}dxdy^{2} + \frac{\partial^{3} u}{\partial y^{3}}dy^{3} $
一般的
$ d^{n}u = \frac{\partial^{n} u}{\partial x^{n}}dx^{n} + \cdots + {n \choose k} \frac{\partial^{n} u}{\partial x^{k} \partial y^{n-k}} dx^{k}dy^{n-k} + \cdots + \frac{\partial^{n} u}{\partial y^{n}}dy^{n} $
这样
$ d^{n} u = (\frac{\partial}{\partial x}dx + \frac{\partial}{\partial y}dy)^{n} u $
三个以上的变量的话,同样的
$ \begin{aligned} d^{2} u &= \frac{\partial^{2} u}{\partial x^{2}} dx^{2} + \frac{\partial^{2} u}{\partial y^{2}}dy^{2} + \frac{\partial^{2}u}{\partial z^{2}}dz^{2} + \cdots &+ 2 \frac{\partial^{2} u}{\partial x \partial y}dxdy + 2 \frac{\partial^{2} u}{\partial x \partial y} + 2 \frac{\partial^{2} u}{\partial x \partial z}dxdz + 2 \frac{\partial^{2} u}{\partial y \partial z}dydz + \cdots , \end{aligned} $
一般的
$ d^{n}u = (\frac{\partial}{\partial x}dx + \frac{\partial}{\partial y}dy + \frac{\partial}{\partial z}dz + \cdots)^{n} u $
合成函数 u为x, y的函数,x, y为t的函数,u为t的函数
u跟x, y相关,x, y跟t相关连续(可微分)的话,u连续(可微分)
可微分的时候 $ \frac{du}{dt} $得
$ \Delta u = u_ {x} \Delta x + u_ {y} \Delta y + o(\sqrt{\Delta x^{2} + \Delta y^{2}}) $
$ \Delta x, \Delta y $使得 $ \Delta t $对应变化
$ \Delta x = x^{\prime} \Delta t + o(\Delta t), \qquad \Delta y = y^{\prime} \Delta t + o(\Delta t) $
综合得
$ \Delta u = (u_ {x}x^{\prime} + u_ {y}y^{\prime}) \Delta t + o(\Delta t) $
$ \lim_ {\Delta t \to 0} \frac{\Delta u}{\Delta t} $存在,这样
$ \frac{du}{dt} = u_ {x}x^{\prime} + u_ {y}y^{\prime}. \qquad (x^{\prime} = \frac{dx}{dt}, y^{\prime} = \frac{dy}{dt}) $
第二阶以上可微分的话,有
$ \begin{aligned} \frac{d^{2}u}{dt^{2}} &= \frac{du_ {x}}{dt}x^{\prime} + u_ {x}x^{\prime \prime} + \frac{du_ {y}}{dt}y^{\prime} + u_ {y}y^{\prime \prime} \\ &= (u_ {xx}x^{\prime} +u_ {xy}y^{\prime})x^{\prime} + (u_ {xy}x^{\prime} + u_ {yy}y^{\prime})y^{\prime} + u_ {x}x^{\prime \prime} + u_ {y}y^{\prime \prime} \\ &= u_ {xx}x^{\prime 2} + 2u_ {xy}x^{\prime}y^{\prime} + u_ {yy}y^{\prime 2} + u_ {x}x^{\prime \prime} + u_ {y}y^{\prime \prime} \end{aligned} $
x、y是两个变量 $ \xi, \eta $的函数,u也是 $ \xi, \eta $的函数。这样
$ u_ {\xi} = u_ {x} x_ {\xi} + u_ {y}y_ {\xi}, \qquad u_ {\eta} = u_ {x}u_ {\eta} + u_ {y}y_ {\eta} $
同样的
$ u_ {\xi \xi} = u_ {xx}x^{2}_ {\xi} + 2u_ {xy}x_ {\xi}y_ {\xi} + u_ {yy}y^{2}_ {\xi} + u_ {x}x_ {\xi \xi} + u_ {y}y_ {\xi \xi} $
$ u_ {\xi \eta} = u_ {xx}x_ {\xi}x_ {\eta} + u_ {xy}(x_ {\xi}y_ {\eta} + x_ {\eta}y_ {\xi}) + u_ {yy}y_ {\xi}y_ {\eta} + u_ {x}x_ {\xi \eta} + u_ {y}y_ {\xi \eta} $
$ u_ {\eta \eta} = u_ {xx}x^{2}_ {\eta} + 2u_ {xy}x_ {\eta}y_ {\eta} + u_ {yy}y^{2}_ {\eta} + u_ {x}x_ {\eta \eta} + u_ {y}y_ {\eta \eta} $
例子 u = u(x, y),x,y 相关偏微分商的极坐标变换
$ x = r \cos{\theta}, \qquad y = r \sin{\theta} $
$ r = \sqrt{x^{2} + y^{2}}, \qquad \theta = \arctan{\frac{y}{x}} $
u是r, $ \theta $的函数,$ r, \theta $是x, y的函数,计算得
$ r_ {x} = \frac{x}{r} = \cos{\theta}, \qquad r_ {y} = \frac{y}{r} = \sin{\theta} $
$ \theta_ {x} = - \frac{y}{r^{2}} = - \frac{\sin{\theta}}{r}, \qquad \theta_ {y} = \frac{x}{r^{2}} = \frac{\cos{\theta}}{r} $
$ u_ {x} = u_ {r}r_ {x} + u_ {\theta}\theta_ {x} = u_ {r}\cos{\theta} - \frac{u_ {\theta}}{r} \sin{\theta} $
$ u_ {y} = u_ {r}r_ {y} + u_ {\theta}\theta_ {y} = u_ {r} \sin{\theta} + \frac{u_ {\theta}}{r} \cos{\theta} $
$ u_ {xx} = u_ {rr}\cos^{2}{\theta} + \frac{u_ {\theta \theta}}{r^{2}} \sin^{2}{\theta} - 2 \frac{u_ {r\theta}}{r} \cos{\theta} \sin{\theta} + \frac{u_ {r}}{r} \sin^{2}{\theta} + 2 \frac{u_ {\theta}}{r^{2}} \cos{\theta} \sin{\theta} $
$ u_ {yy} = u_ {rr}\sin^{2}{\theta} + \frac{u_ {\theta \theta}}{r^{2}} \cos^{2}{\theta} + 2 \frac{u_ {r\theta}}{r} \cos{\theta} \sin{\theta} + \frac{u_ {r}}{r} \cos^{2}{\theta} - 2 \frac{u_ {\theta}}{r^{2}} \cos{\theta} \sin{\theta} $
这样
$ \frac{\partial^{2}u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} = \frac{\partial^{2} u}{\partial r^{2}} + \frac{1}{r^{2}} \frac{\partial^{2} u}{\partial \theta^{2}} + \frac{1}{r} \frac{\partial u}{\partial r} $
Taylor公式
固定差异 对于y = f(x),x一定的增量 $ \Delta x(\Delta x \ge 0) $,对于y的增量
$ \Delta y = \Delta f(x) = f(x + \Delta x) - f(x) $
为y的定差的差分。$ \Delta y $是x的函数,对应 $ \Delta x $的增加,这样的固定差异为y的第二阶定差,记为 $ \Delta^{2} y $
$ \begin{aligned} \Delta^{2} y &= \Delta f(x + \Delta x) - \Delta f(x) \\ &= \{f(x + 2 \Delta x) - f(x + \Delta x)\} - \{f(x + \Delta x) - f(x)\} \\ &= f(x + 2 \Delta x) - 2f(x + \Delta x) + f(x) \end{aligned} $
同样的,第n阶的定差
$ \begin{aligned} \Delta^{n} y &= \Delta^{n-1}f(x + \Delta x) - \Delta^{n-1}f(x) \\ &= f(x + n \Delta x) - {n \choose 1} f(x + (n-1) \Delta x) + {n \choose 2}f(x + (n-2) \Delta x) + \cdots + (-1)^{n} f(x) \end{aligned} $
例如,$ g(x) = ax^{n} + \cdots $为n的多项式,$ \Delta x = h $
$ \Delta g(x) = nahx^{n-1} + \cdots, \qquad \Delta^{2}g(x) = n(n-1)ah^{2}x^{n-2} + \cdots $
$ \Delta^{n} g(x) = n! ah^{n} \qquad \Delta^{n+1} g(x) = 0 $
则对十分小的 $ \Delta x $
$ f(x + k \Delta x) = \sum^{n}_ {\nu = 0}(k \Delta x)^{\nu} \frac{f^{(\nu)}(x)}{\nu !} + o(\Delta x)^{n} $
这样
$ \begin{aligned} \Delta^{n} y &= \sum^{n}_ {k, \nu = 0}(-1)^{n-k} {n \choose k} k^{\nu} \Delta x^{\nu} \frac{f^{(\nu)}(x)}{\nu !} + o(\Delta x)^{n} \\ &= \sum^{n}_ {\nu = 0} \Delta x^{\nu} \frac{f^{(\nu)}(x)}{\nu !} (\sum^{n}_ {k=0} (-1)^{n-k} {n \choose k}k^{\nu}) + o(\Delta x)^{n} \end{aligned} $
现在
$ \sum^{n}_ {k=0}(-1)^{k}{n \choose k}k^{\nu} = \left\{ \begin{array}{ll} 0, & (\nu = 0, 1, \ldots, n-1) \\ (-1)^{n} n! & (\nu = n) \end{array} \right. $
这样 $ y = x^{n} $,从以上的式子及 $ \Delta^{n} y = n! \Delta x^{n} $有
$ \Delta^{n} y = (\Delta x)^{n} f^{(n)}(x) + o(\Delta x)^{n} $
从而
$ \lim_ {\Delta x \to 0} \frac{\Delta^{n} y}{\Delta x^{n}} = f^{(n)}(x) $
二元以上的Taylor公式 f(x, y) n次可微分时A = (x, y)区域内一点,取很小的 $ | h |, | k | $,点B = (x+h, y+k)的线分AB有
$ F(t) = f(x + ht, y + kt) $
$ 0 \le t \le 1 $区间里t的函数,有
$ F^{\prime}(t) = (h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y}) f(x + ht, y + kt), \ldots, $
$ F^{n}(t) = (h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y})^{n} f(x+ht, y+kt) $
有
$ F(t) = F(0) + tF^{\prime}(0) + \cdots + \frac{t^{n-1}}{(n-1)!} F^{(n-1)}(0) + \frac{t^{n}}{n!} F^{(n)}(\theta t), \qquad 0 < \theta < 1 $
t = 1时
$ \begin{aligned} f(x+h, y+k) &= f(x,y) + df(x, y) + \frac{1}{2} d^{2} f(x, y) + \cdots \\ &+ \frac{1}{(n-1)!} d^{n-1} f(x, y) + \frac{1}{n!} d^{n} f(x + \theta h, y + \theta k) \end{aligned} $
用 $ d^{\nu} $简记为
$ df(x, y) = hf_ {x}(x, y) + kf_ {y}(x, y) $
$ d^{2} f(x, y) = h^{2} f_ {xx}(x,y) + 2hkf_ {xy}(x, y) + k^{2}f_ {yy}(x, y), \ldots $
最后的剩余项变量x, y用 $ x + \theta h, y + \theta k $带入
当n = 1时
$ f(x + h, y + k) - f(x, y) = hf_ {x}(x + \theta h, y + \theta k) + kf_ {y}(x + \theta h, y + \theta k) $
$ (x + \theta h, y + \theta k) $为线分AB上的点。这是二元的平均值定理
对点A = (x, y)第n阶微分,假定可能性
$ f(x + h, y + k) = f(x, y) + df(x, y) + \frac{d^{2} f(x, y)}{2!} + \cdots + \frac{d^{n} f(x, y)}{n!} + o \rho^{n} $
$ \rho = \sqrt{h^{2} + k^{2}} $
这样证明
$ F(t) = f(x + \frac{h}{\rho} t, y + \frac{k}{\rho} t) $
则
$ F(t) = F(0) + tF^{\prime}(0) + \cdots + \frac{t^{n} F^{(n)}(0)}{n!} + ot^{n} $
$ t = \rho $,这样 $ ot^{n} / t^{n} $AB线分的方向无关收敛
Taylor级数 如果f(x)各阶微分存在的话,区间内关于x
$ lim_ {n \to \infty}R_ {n} = 0 $
则
$ f(x) = lim_ {n \to \infty} \sum^{n}_ {\nu = 0}(x - a)^{\nu} \frac{f^{(\nu)}(a)}{\nu !} $
右边用无限级数写成为
$ f(x) = f(a) + (x - a)\frac{f^{\prime}(a)}{1!} + (x - a)^{2} \frac{f^{\prime \prime}(a)}{2!} + \cdots + (x - a)^{n} \frac{f^{(n)}(a)}{n!} + \cdots $
这样的形式是f(x)的Taylor级数。特别地a = 0时被称为Maclaurin级数
例子 $ f(x) = e^{x} $
a = 0且 $ f^{(n)} = 1 $则
$ R_ {n} = \frac{x^{n}}{n!} e^{\theta x}, \qquad 0 < \theta < 1 $
则
$ | R_ {n} | < \frac{| x |^{n}}{n!} e^{| x |} $
固定x则 $ \lim \frac{| x |^{n}}{n!} = 0 $,则 $ - \infty < x < \infty $
$ e^{x} = 1 + \frac{x}{1!} + \frac{x^{2}}{2!} + \cdots + \frac{x^{n}}{n!} + … $
特别当x = 1时,剩余项写入得
$ e = 1 + \frac{1}{1!} + \frac{1}{2!} + \cdots + \frac{1}{n!} + R_ {n+1}, \qquad R_ {n+1} = \frac{e^{\theta}}{(n+1)!} < \frac{3}{(n+1)!} $
e的计算 e是 $ lim{(1 + \frac{1}{n})^{n}} $,现在用 $ \frac{1}{n!} $小数第7位数计算,到n = 10有
$ \begin{aligned} 1 + \frac{1}{1!} + \frac{1}{2!} &= 2.5 \\ \frac{1}{3!} &= 0.1666666 \\ \frac{1}{4!} &= 0.0416666 \\ \frac{1}{5!} &= 0.0083333 \\ \frac{1}{6!} &= 0.0013888 \\ \frac{1}{7!} &= 0.0001984 \\ \frac{1}{8!} &= 0.0000248 \\ \frac{1}{9!} &= 0.0000027 \\ \frac{1}{10!} &= 0.0000002 \\ e &= 2.7182814 \end{aligned} $
这样得到e的近似值,$ n \ge 3 $有8项误差大于 $ \frac{1}{10^{7}} $,剩余项
$ R_ {11} < \frac{3}{11!} = \frac{1}{10!} \frac{3}{11} < \frac{1}{10^{7}} $
误差小于 $ \frac{1}{10^{6}} $,实际上 $ e = 2.718281828 \cdots $
e为无理数的证明 假设e是有理数,$ e = \frac{m}{n} $,m, n为整数,则 $ n! e $为整数,从而
$ n! R_ {n+1} = \frac{e^{\theta}}{n + 1} > 0 \qquad (0 < \theta < 1) $
必须为整数。从而
$ 1 \le \frac{e^{\theta}}{n+1} < \frac{3}{n+1} $
则 n + 1 < 3, n < 2, n = 1。然而e = m,则e必须是整数,而由于2 < e < 3,则矛盾
例子 $ \sin{x} = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - + \cdots $
$ \cos{x} = 1 - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} -+ \cdots $
x任意,这样 $ | R_ {n} | \to 0 $
极大极小
函数f(x)在点 $ x = x_ {0} $取值为 $ f(x_ {0}) $,其是 $ x_ {0} $的附近的值大(小),则 $ f(x_ {0}) $为最大值(最小值),$ x_ {0} $为f(x)的极大点(极小点),最大值、最小值统称为极值,这样 $ x_ {0} $为极值点
$ x_ {0} $为f(x)的极小点,则
$ 0 < | x - x_ {0} | < \delta \text{ 时 } f(x) - f(x_ {0}) > 0 $
如果把上式中的>换成 $ \ge $,则 $ f(x_ {0}) $ 为弱极小值
定理 点 $ x_ {0} $为函数f(x)定义域内一点
(1) f(x)在 $ x_ {0} $可微分时,$ x = x_ {0} $如果是f(x)的极值,则 $ f^{\prime}(x_ {0}) = 0 $。$ f^{\prime}(x_ {0}) $存在是极值的必要条件
(2) f(x)在 $ x_ {0} $处连续,$ x_ {0} $附近可微分,如果 $ f^{\prime}(x) $在 $ x = x_ {0} $处符号改变,$ f(x_ {0}) $为极值。详细地说,x逐渐增大地通过 $ x_ {0} $,$ f^{\prime} $符号从+变成-,则 $ f(x_ {0}) $为极大值,如果是从-变成+则是极小值
(3) f(x)在 $ x_ {0} $附近可微分,$ f^{\prime \prime}(x_ {0}) $存在,$ f^{\prime}(x_ {0}) = 0, f^{\prime \prime}(x_ {0}) > 0 $则 $ f(x_ {0}) $为极小值,$ f^{\prime}(x_ {0}) = 0, f^{\prime \prime}(x_ {0}) < 0 $则 $ f(x_ {0}) $为极大值
例子 一个平面两侧的亮点A, B,动点P在这个平面的两侧以一定的速度 $ c_ {1}, c_ {2} $运动,P从A到B最短的运动时间是什么?
解答 问题的要求是P需要在平面的两侧沿直线运动,问题简化如下
平面的直角坐标x轴上侧和下侧的点 $ A = (0, h_ {1}), B = (a, -h_ {2}), a > 0 $。P = (x, 0),则求使 $ \frac{AP}{c_ {1}} + \frac{BP}{c_ {2}} $值最小的P点位置
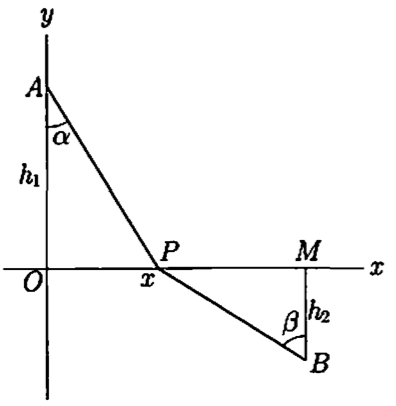
则可认为是区间为 $ 0 \le x \le a $的
$ f(x) = \frac{\sqrt{h^{2}_ {1} + x^{2}}}{c_ {1}} + \frac{\sqrt{h^{2}_ {2} + (a-x)^{2}}}{c_ {2}} $
的最小值
上述区间内,f(x)可微分,计算得
$ f^{\prime}(x) = \frac{1}{c_ {1}} \cdot \frac{x}{\sqrt{h^{2}_ {1} + x^{2}}} - \frac{1}{c_ {2}} \cdot \frac{a - x}{\sqrt{h^{2}_ {2} + (a-x)^{2}}} $
考察 $ f^{\prime}(x) = 0 $
$ f^{\prime}(x) $的第一项
$ \frac{1}{c_ {1}} \frac{x}{\sqrt{h^{2}_ {1} + x^{2}}} = \frac{\sin{\alpha}}{c_ {1}} $
这里$ [0, a] $区间x增大则单调增大,而第二项
$ \frac{1}{c_ {2}} \frac{a-x}{\sqrt{h^{2}_ {2} + (a - x)^{2}}} = \frac{\sin{\beta}}{c_ {2}} $
x增大则单调减小
则点 $ x_ {0} $应该是
$ \frac{\sin{\alpha}}{\sin{\beta}} = \frac{c_ {1}}{c_ {2}} \qquad \text{光的折射率} $
多变量的极值定义 两变量的 $ P_ {0} = (x_ {0}, y_ {0}) $的附近,$ P_ {0} $之外的点P = (x, y)
$ f(P) < f(P_ {0}) \qquad f(P) > f(P_ {0}) $
则 $ f(P_ {0}) $为极大(极小)值
这样的定义,$ f(x_ {0}, y_ {0}) $的极值,有
$ f_ {x}(x_ {0}, y_ {0}) = 0, \qquad f_ {y}(x_ {0}, y_ {0}) = 0 $
这是极值的必要条件
这样的条件下
$ f(x, y) - f(x_ {0}, y_ {0}) = \frac{1}{2} \{ a(x - x_ {0})^{2} + 2b(x - x_ {0})(y - y_ {0}) + c(y - y_ {0})^{2} \} + o \rho^{2} $
$ a = f_ {xx}(x_ {0}, y_ {0}), b = f_ {xy}(x_ {0}, y_ {0}), c = f_ {yy}(x_ {0}, y_ {0}), \rho = \sqrt{(x - x_ {0})^{2} + (y - y_ {0})^{2}} $
$ \rho $非常小,上式右边的符号决定了二次式
$ aX^{2} + 2bXY + cY^{2} \qquad (X = x - x_ {0}, Y = y - y_ {0}) $
这样有三种情况
(1) $ ac - b^{2} > 0 $。由二次式的符号,a和c的正负符号相同,a为正则是极小值,否则为极大值
(2) $ ac - b^{2} < 0 $。$ P_ {0} $的附近 $ f(P) > f(P_ {0}), f(P) < f(P_ {0}) $都有,$ f(P_ {0}) $不是极值
(3) $ ac - b^{2} = 0 $。这种情况下,需要考虑三阶及以上微分,但是用一般的理论相当复杂,现在为了简单起见,坐标进行变换,$ (x_ {0}, y_ {0}) = (0, 0) $,这样的情况是一个完全平方形,用a = 0, b = 0, c = 1做二三个例子
例1 $ z = y^{2} $。在(0, 0)点是z的最小值0,(x, 0)时z = 0,这是极小值
例2 $ z = y^{2} + x^{4} $。(0, 0)点极小值
例3 $ z = y^{2} - x^{3} $。(0, 0)点不是极值点,(x, y)下图左图,阴影部分z < 0,其他部分则z > 0
例4 $ z = (y - x^{2})(y - 2x^{2})。同上,下图右图
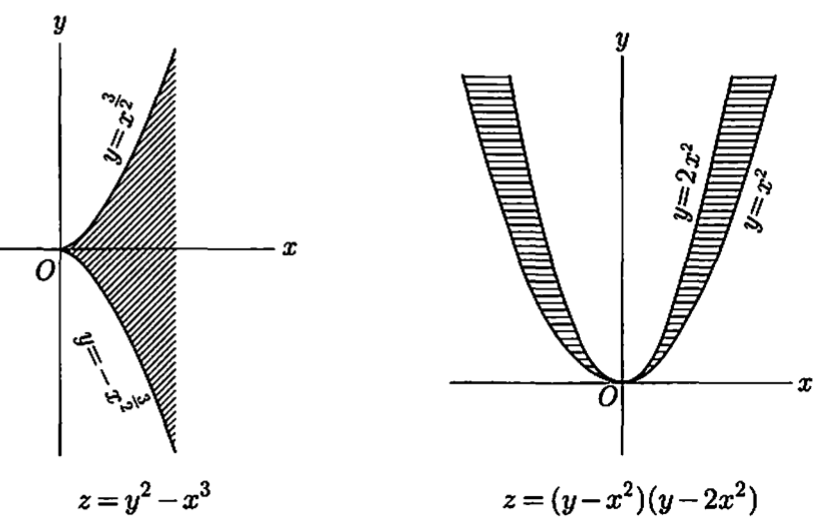
有三个以上变量的情况,$ f(x_ {1}, x_ {2}, \cdots, x_ {n}) $关于点 $ A = (a_ {1}, a_ {2}, \ldots, a_ {n}) $为极值的话,这样的点
$ f_ {x_ {1}} = 0, f_ {x_ {2}} = 0, \cdots, f_ {x_ {n}} = 0 $
为必要的,这样的话关于A $ f_ {x_ {i}x_ {j}}(A) = a_ {ij} $
$ f(a_ {1} + \xi_ {1}, \cdots, a_ {n} + \xi_ {n}) - f(a_ {1}, \cdots, a_ {n}) = \frac{1}{2} Q(\xi_ {1}, \xi_ {2}, \cdots, \xi_ {n}) + o \rho^{2} $
$ Q(\xi_ {1}, \xi_ {2}, \cdots, \xi_ {n}) = \sum^{n}_ {i, j = 1}a_ {ij}\xi_ {i}\xi_ {j} $
$ \rho = \sqrt{\sum^{n}_ {i=1} \xi^{2}_ {i}} $
$ a_ {ij} $的行列式为
$ D = \left | \begin{array}{cccc} a_ {11} & a_ {12} & \cdots & a_ {1n} \\ a_ {21} & a_ {22} & \cdots & a_ {2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_ {n1} & a_ {n2} & \cdots & a_ {nn} \end{array} \right | \ne 0 \qquad (a_ {ij} = a_ {ji}) $
这样我们可以对A是否有极值点做断言
如果二次形式Q符号固定,则为正时极小,负时极大。它的判别法可通过D的前导行列式的符号获得。$ D_ {k} $全为正时极小,$ D_ {k} $的符号为 $ (-1)^{k} $时极大
二次形式Q符号不固定时,f(A)没有极值。$ D \ne 0 $时,$ D_ {k} $不符合上述条件,就可能会这样
D = 0时,只有二阶微分时不能断言
例子 求给定周长的三角形的最大面积
解 周长为2p,边为x, y, z,面积为S,S用f(x, y)带入得
$ f(x, y) = p(p - x)(p - y)(p -z), \qquad z = 2p - x - y $
独立变量为x,y,其变动范围为
$ 0 < x < p, \qquad, 0 < y < p, \qquad p < x + y $
这样固定三角形的一条边y,则从几何学上我们可知最大面积为x = z时。这样 $ f_ {x} = 0 $,同样 $ f_ {y} = 0 $时y = z。这样
$ x = y = z = \frac{2}{3} p $

从这个关系我们得出一个正的直角三角形,但这是不可能的。我们知道“如果有一个最大值,它是一个等边三角形“,由于f(x, y)是连续的,但它不是闭区间,不能保证最大值的存在,这是问题的关键
幸好根据Weierstrass定理,我们可以越过这个障碍,我们构造一个封闭区域
$ 0 \le x \le p, \qquad 0 \le y \le p \qquad p \le x + y $
在三角形的极端情况下,它只不过是一条双线段,因此即使是面积为0的线段也参与了最大值的竞争。现在在这个封闭区间中有最大值。然而,在区间的边界处f = 0,在区域内f > 0。因此最大值在区域内部,则 $ x = y = z = \frac{2}{3} p $时是最大值
我们计算这里的二阶导数,我们使用上一节的符号
$ a = c = - \frac{2}{3} p^{2}, \qquad b = - \frac{1}{3} p^{2}, \qquad ac - b^{2} > 0 $
则这是极大值点,但极大值不是最大值,所以这个不能解决问题
例子 行列式的最大值(Hadamard定理)。例如,n阶行列式
$ D = \left| \begin{array}{cccc} a_ {1} & b_ {1} & \cdots & l_ {1} \\ a_ {2} & b_ {2} & \cdots & l_ {2} \\ \cdots & \cdots & \cdots & \cdots \\ a_ {n} & b_ {n} & \cdots & l_ {n} \end{array} \right| $
的绝对值的最大值
$ a^{2}_ {i} + b^{2}_ {i} + \cdots + l^{2}_ {i} = s^{2}_ {i} \qquad (i = 1, 2, \cdots, n) $
要求这个条件下。(但是 $ s_ {i} $是正数),目标有以下关系表达式
$ | D | \le s_ {1} s_ {2} \cdots s_ {n} $
D是 $ n^{2} $个变量 $ a_ {1}, \cdots, l_ {n} $的多项式。这种条件下独立变量有n(n - 1)个。现在考察n次元球面上的点 $ P_ {i} $
$ P = (P_ {1}, P_ {2}, \cdots, P_ {n}) $
的组合P的函数的行列式,D = D(P)是关于P连续,P变量变动的闭区间,这样这样的点都是内点。D的最大值、最小值存在,这样可从哪个D的极值中找到
$ D = a_ {i}A_ {i} + b_ {i}B_ {i} + \cdots + l_ {i}L_ {i} $
$ A_ {i}, B_ {i}, \cdots, L_ {i} $是 $ a_ {i}, b_ {i}, \cdots, l_ {i} $的余因子,这样D的第i行以外的组成的多项式,D的极值的必要条件是
$ \frac{\partial D}{\partial a_ {i}} = A_ {i} + L_ {i} \frac{\partial l_ {i}}{\partial a_ {i}} = A_ {i} - L_ {i}\frac{a_ {i}}{l_ {i}} = 0 $
$ b_ {i}, c_ {i}, \cdots $相关也相同,则
$ \frac{A_ {i}}{a_ {i}} = \frac{B_ {i}}{b_ {i}} = \cdots = \frac{L_ {i}}{l_ {i}} $
$ i \ne k $有
$ a_ {k}A_ {i} + b_ {k}B_ {i} + \cdots + l_ {k}L_ {i} = 0 $
则有
$ a_ {i}a_ {k} + b_ {i}b_ {k} + \cdots + l_ {i}l_ {k} = 0 $
由以上的式子的值,D的绝对值已确定。这样
$ D^{2} = \left| \begin{array}{cccc} s^{2}_ {1} & 0 & \cdots & 0 \\ 0 & s^{2}_ {2} & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & s^{2}_ {n} \end{array} \right| = (s_ {1}s_ {2} \cdots s_ {n})^{2} $
则
$ D = \pm s_ {1} s_ {2} \cdots s_ {n} $
这样D的最大值为 $ s_ {1}s_ {2} \cdots s_ {n} $(最小值为 $ - s_ {1}s_ {2}\cdots s_ {n} $ ),这是它的极大极小值
切线和曲率
本章的最后我们讨论切线和曲率,这是微分法的起源。为了简化描述,使用矢量法的记号,矢量作为具有一定大小和方向的量是已知的。从直角坐标原点O到点P = (x, y, z)的线段OP所表示的向量用 $ \upsilon = (x, y, z) $表示,$ | \upsilon | = \sqrt{x^{2} + y^{2} + z^{2}} $
两个向量 $ u = (x_ {1}, y_ {1}, z_ {1}), \upsilon = (x_ {2}, y_ {2}, z_ {2}) $,定义两种乘法
(1) 标量乘法
$ u \upsilon = x_ {1}x_ {2} + y_ {1}y_ {2} + z_ {1}z_ {2} $
$ u, \upsilon $不为零向量时,它们的方向余弦
$ \frac{x_ {1}}{| u |}, \frac{y_ {1}}{| u |}, \frac{z_ {1}}{| u |}, \frac{x_ {2}}{| \upsilon |}, \frac{y_ {2}}{| \upsilon |}, \frac{z_ {2}}{| \upsilon |} $
$ u, \upsilon $间的夹角为 $ \theta $
$ \cos{\theta} = \frac{x_ {1}x_ {2} + y_ {1}y_ {2} + z_ {1}z_ {2}}{| u | | \upsilon |} $
则
$ u \upsilon = | u | | \upsilon | \cos{\theta} $
这是标量乘积几何上的意义。$ u, \upsilon $互相垂直时
$ u \upsilon = 0 $
及
$ uu = x^{2}_ {1} + y^{2}_ {1} + z^{2}_ {1} = | u |^{2} $
对于标量积,交换律和分配律成立
$ u \upsilon = \upsilon u, \qquad (u_ {1} + u_ {2}) \upsilon = u_ {1} \upsilon + u_ {2} \upsilon $
x,y,z为变量t的函数时,向量
$ OP = u = (x, y, z) $
这时,$ t + \Delta t $对应的向量
$ OP^{\prime} = u + \Delta u = (x + \Delta x, y + \Delta y, z + \Delta z) $
则 $ \Delta u $是向量 $ PP^{\prime} $
$ \Delta u = (\Delta x, \Delta y, \Delta z) $
x,y,z可微分的话,$ \Delta t \to 0 $时向量
$ \frac{\Delta u}{\Delta t} = (\frac{\Delta x}{\Delta t}, \frac{\Delta y}{\Delta t}, \frac{\Delta z}{\Delta t}) $
的极限值是一个常量。这样的极限值 $ \dot{u} = \frac{du}{dt} $写为
$ \dot{u} = (\dot{x}, \dot{y}, \dot{z}) $
由向量积的定义,有
$ \frac{d}{dt} (u \upsilon) = \dot{u} \upsilon + u \dot{\upsilon} $
特别地,u常常是单位向量( $ | u | = 1 $),这样当只有方向改变时,uu = 1,$ u \dot{u} = 0 $,这里 $ \dot{u} \ne 0 $时,u和 $ \dot{u} $相互垂直
(2) 向量积 $ u \times \upsilon $,两个向量
$ u = (x_ {1}, y_ {1}, z_ {1}), \upsilon = (x_ {2}, y_ {2}, z_ {2}) $
坐标的行列
$ \left( \begin{array}{ccc} x_ {1} & y_ {1} & z_ {1} \\ x_ {2} & y_ {2} & z_ {2} \end{array} \right) $
坐标为三个行列式的向量
$ \omega = (y_ {1}z_ {2} - y_ {2}z_ {1}, z_ {1}x_ {2} - z_ {2}x_ {1}, x_ {1}y_ {2} - x_ {2}y_ {1}) $
这个是 $ u, \upsilon $的向量积,写为 $ u \times \upsilon $。其几何学的意义如下
现在简单的 $ \omega = (x, y, z) $写为
$ xx_ {1} + yy_ {1} + zz_ {1} = 0, \qquad xx_ {2} + yy_ {2} + zz_ {2} = 0 $
即
$ \omega u = 0, \qquad \omega \upsilon = 0 $
则 $ \omega $ 与u 和 $ \upsilon $相互垂直
$ \left | \begin{array}{ccc} x & y & z \\ x_ {1} & y_ {1} & z_ {1} \\ x_ {2} & y_ {2} & z_ {2} \end{array} \right | = x^{2} + y^{2} + z^{2} = | \omega |^{2} $
是一个平行六面体的体积,它的三条边为向量u, $ \upsilon, \omega $,因为它是正的,所以$ u, \upsilon, \omega $是一个与坐标轴一致的系统(右手螺旋),由于它的体积等于 $ | \omega |^{2} $,$ | \omega | $为 $ u, \upsilon $为边的平行四边形的面积
特别地当 $ u, \upsilon $方向一致时
$ u \times \upsilon = 0 $
根据上面的定义,向量积的交换律不成立
$ u \times \upsilon = - \upsilon \times u $
有分配律
$ (u_ {1} + u_ {2}) \times \upsilon = u_ {1} \times \upsilon + u_ {2} \times \upsilon $
$ \upsilon \times (u_ {1} + u_ {2}) = \upsilon \times u_ {1} + \upsilon \times u_ {2} $
$ u, \upsilon $为t的函数时
$ \frac{d}{dt} (u \times \upsilon) = \dot{u} \times \upsilon + u \times \dot{\upsilon} $
(3) 此外,三个向量
$ u = (x_ {1}, y_ {1}, z_ {1}), \qquad \upsilon = (x_ {2}, y_ {2}, z_ {2}), \qquad \omega = (x_ {3}, y_ {3}, z_ {3}) $
平行六面体的体积由 $ (u, \upsilon, \omega) $来表示
$ (u, \upsilon, \omega) = \left | \begin{array}{ccc} x_ {1} & y_ {1} & z_ {1} \\ x_ {2} & y_ {2} & z_ {2} \\ x_ {3} & y_ {3} & z_ {3} \end{array} \right | $
如果三个单位向量i, j, k(两两互相垂直)是右旋螺旋,则它们构成一个单位系统,在这种情况下
$ i^{2} = j^{2} = k^{2} = 1, \qquad i \times i = j \times j = k \times k = 0 $
$ ij = ji = 0, \qquad i \times j = k = -j \times i $
$ jk = kj = 0, \qquad j \times k = i = -k \times j $
$ ki = ik = 0, \qquad k \times i = j = - i \times k $
$ (i, j, k) = 1 $
现在曲线C用变量t来表示,C上的点P = (x, y, z)的坐标x, y, z是t的函数,向量OP用 $ \upsilon $表示,现在曲线上 $ t + \Delta t $对应的点 $ P^{\prime} = (x + \delta x, y + \delta y, z + \delta z) $,则向量 $ OP^{\prime} $为 $ \upsilon + \delta \upsilon $,则 $ \delta \upsilon $为向量 $ PP^{\prime} $
$ \delta \upsilon = (\delta x, \delta y, \delta z) $
现在x, y, z三阶可微分的话,则泰勒公式
$ \delta x = \dot{x} \delta t + \ddot{x} \frac{\delta t^{2}}{2} + \dddot{x}\frac{\delta t^{3}}{6} + o \delta t^{3} $
$ \delta y, \delta z $也一样,这样可写为
$ \delta \upsilon = \dot{\upsilon} \delta t + \ddot{\upsilon} \frac{\delta t^{2}}{2} + \dddot{\upsilon} \frac{\delta t^{3}}{6} + o \delta t^{3} $
$ \dot{\upsilon} = (\dot{x}, \dot{y}, \dot{z}) $,$ \ddot{\upsilon}, \dddot{\upsilon} $也一样,$ \delta t \to 0 $时 $ | o | \to 0 $,$ \dot{\upsilon}, \ddot{\upsilon}, \dddot{\upsilon} $三个向量关于曲线上点P在几何学上有重要的性质
对向量 $ \dot{\upsilon} = (\dot{x}, \dot{y}, \dot{z}) $,
$ | \dot{\upsilon} | = \sqrt{\dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2}} $
点P在曲线C的切线的方向余弦为
$ \frac{\cos{\alpha}}{\dot{x}} = \frac{\cos{\beta}}{\dot{y}} = \frac{\cos{\gamma}}{\dot{z}} = \frac{1}{| \dot{\upsilon} |} $
但是 $ \dot{\upsilon} = 0 $时,要排除 $ \dot{x}, \dot{y}, \dot{z} $同时为0的点(特异点)
如果以曲线C的一个固定点计算的弧长s代替t作为参赛,则结果很简明
$ \delta \upsilon = \upsilon^{\prime} \delta s + \upsilon^{\prime \prime} \frac{\delta s^{2}}{2} + \upsilon^{\prime \prime \prime} \frac{\delta s^{3}}{6} + o \delta s^{3} $
弧长理论将在后面介绍,这里弧 $ PP^{\prime} $和弦 $ PP^{\prime} $的比在距离 $ PP^{\prime} \to 0 $时收敛到1,即
$ \frac{\delta x^{2} + \delta y^{2} + \delta z^{2}}{\delta s^{2}} \to 1 $
则
$ \frac{dx}{ds} = \cos{\alpha}, \qquad \frac{dy}{ds} = \cos{\beta}, \qquad \frac{dz}{ds} = \cos{\gamma} $
则有
$ x^{\prime 2} + y^{\prime 2} + z^{\prime 2} = 1 \Rightarrow | \upsilon^{\prime} | = 1 $
s为变量,$ \upsilon^{\prime} $切线上关于s的增加方向上取的单位向量。$ | \upsilon^{\prime} | = 1 $的话,假定$ \upsilon^{\prime \prime} \ne 0 $,则 $ \upsilon^{\prime \prime} $和 $ \upsilon^{\prime} $垂直。P上关于 $ \upsilon^{\prime \prime} $平行的直线是曲线C的主法线,含有$ \upsilon^{\prime}, \upsilon^{\prime \prime} $的平面是接触平面
通过P点的任意平面的方程式的标准形为
$ l(X - x) + m(Y - y) + n(Z - z) = 0 \qquad (l^{2} + m^{2} + n^{2} = 1) $
p = (l, m, n)是平面的法线上的单位向量。曲线上的点 $ P^{\prime} = (x + \delta x, y + \delta y, z + \delta z) $到平面的距离为
$ l\delta x + m \delta y + n \delta z $
等于 $ p \cdot \delta \upsilon $的标量积。但 $ \delta \upsilon = (\delta x, \delta y, \delta z) $,这样
$ p \upsilon^{\prime} \delta s + p \upsilon^{\prime \prime} \frac{\delta s^{2}}{2} + o \delta s^{2} $
p和 $ \upsilon^{\prime}, \upsilon^{\prime \prime} $垂直,即含有$ \upsilon^{\prime}, \upsilon^{\prime \prime} $的平面时$ \delta \upsilon $为高位的小数。这就意味着是接触平面
设P关于$ P^{\prime} $切线间的夹角为 $ \alpha $,$ \delta \alpha $为向量 $ \upsilon^{\prime}, \upsilon^{\prime} + \delta \upsilon^{\prime} $间的夹角,$ \upsilon^{\prime} $的长为常量1时,$ \delta s \to 0 $
$ \frac{\delta \alpha}{| \delta \upsilon^{\prime} |} \to 1 $
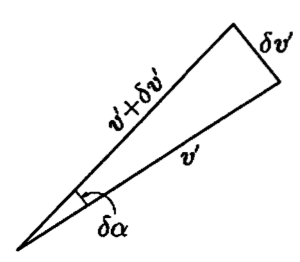
然而
$ \frac{\delta \upsilon^{\prime}}{\delta s} \to \upsilon^{\prime \prime}, \qquad \frac{| \delta \upsilon^{\prime} |}{\delta s} \to | \upsilon^{\prime \prime} | $
则有
$ \frac{\delta \alpha}{\delta s} \to | \upsilon^{\prime \prime} | \Rightarrow \frac{d \alpha}{d s} = | \upsilon^{\prime \prime} | $
这里 $ \frac{d \alpha}{ds} $为C的切线方向随弧长变动的改变率,这里点P上的曲率,它的倒数 $ \rho $为曲率半径。即
$ \frac{1}{\rho} = \frac{d \alpha}{ds} = | \upsilon^{\prime \prime} | = \sqrt{(\frac{d^{2}x}{ds^{2}})^{2} + (\frac{d^{2}y}{ds^{2}})^{2} + (\frac{d^{2}z}{ds^{2}})^{2}} $
这是P上接触平面的垂线即陪法线。现在,切线、主法线、陪法线上单位用i,j,k,记为
$ \left. \begin{array}{l} i = \upsilon^{\prime}, \\ j = \rho \upsilon^{\prime \prime}, \\ k = i \times j. \end{array} \right\} $
然而
$ k^{\prime} = i^{\prime} \times j + i \times j^{\prime} $
有$ i^{\prime} = \upsilon^{\prime \prime} $与j平行,则 $ i^{\prime} \times j = 0 $,从而
$ k^{\prime} = i \times j^{\prime} $
则 $ k^{\prime} $与i垂直。而 $ | k | = 1 $得 $ k^{\prime} $ 与k垂直,从而 $ k^{\prime} $与j平行。(这里假定 $ k^{\prime} \ne 0 $)跟 $ | \upsilon^{\prime \prime} | $一样,$ | k^{\prime} | $是s随陪法线方向的变动率,即接触平面绕切线旋转的角度的变动率。由于将s的增加方向定为切线的正方向,因此这种回旋可以定正负。$ k^{\prime} $与j平行,从$ | j | = 1 $得到 $ k^{\prime} = \pm | k^{\prime} | j $,现在
$ k^{\prime} = - \frac{1}{\tau} j $
$ \frac{1}{\tau} $为切线C的第二曲率即扭率,它的倒数为扭率半径
点P在曲线C上移动时,单位系统(i,j,k)以右手还是左手变动取决于 $ \tau $的正负
任意向量用i,j,k组合表达为ai+bj+ck,现在 $ j^{\prime} $考察
$ j = k \times i, j^{\prime} = k^{\prime} \times i + k \times i^{\prime} $
$ i^{\prime} = \upsilon^{\prime \prime} = \frac{1}{\rho} j, k^{\prime} = - \frac{1}{\tau} j $,则 $ j \times i = -k, k \times j = -i $
$ j^{\prime} = - \frac{1}{\rho} i + \frac{1}{\tau} k $
上述 $ i^{\prime}, j^{\prime}, k^{\prime} $一起写为
$ \left\{ \begin{array}{ccccc} i^{\prime} & = & & \frac{1}{\rho}j, & \\ j^{\prime} & = & - \frac{1}{\rho}i & & + \frac{1}{\tau} k, \\ k^{\prime} & = & & -\frac{1}{\tau} j & \end{array} \right. $
这是Frenet公式,i, j, k的常量部分是切线、主法线、陪法线的方向余弦,$ \prime $是弧长s的微分表示,利用 $ \upsilon^{\prime \prime} = \frac{1}{\rho} j $
$ \begin{aligned} \upsilon^{\prime \prime \prime} &= - \frac{\rho^{\prime}}{\rho^{2}} j + \frac{1}{\rho} j^{\prime} \\ &= - \frac{1}{\rho^{2}} i - \frac{\rho^{\prime}}{\rho^{2}} j + \frac{1}{\rho \tau} k \end{aligned} $
从而
这样作为行列式
$ \begin{aligned} (\upsilon^{\prime}, \upsilon^{\prime \prime}, \upsilon^{\prime \prime \prime}) &= (i, \frac{1}{\rho} j, - \frac{1}{\rho^{2}} i - \frac{\rho^{\prime}}{\rho^{2}}j + \frac{1}{\rho \tau} k) \\ &= (i, \frac{1}{\rho} j, \frac{1}{\rho \tau} k) \\ &= (i, \frac{1}{\rho}j, \frac{1}{\rho \tau}k) = \frac{1}{\rho^{2} \tau}(i, j, k) = \frac{1}{\rho^{2} \tau} \end{aligned} $
从而
$ \frac{1}{\tau} = \rho^{2} (\upsilon^{\prime}, \upsilon^{\prime \prime}, \upsilon^{\prime \prime \prime}) = \frac{\left| \begin{array}{ccc} x^{\prime} & y^{\prime} & z^{\prime} \\ x^{\prime \prime} & y^{\prime \prime} & z^{\prime \prime} \\ x^{\prime \prime \prime} & y^{\prime \prime \prime} & z^{\prime \prime \prime} \end{array} \right |}{x^{\prime \prime 2} + y^{\prime \prime 2} + z^{\prime \prime 2}} $
这是s作为变量的扭率
任意变量t相关 $ \rho, \tau $计算,t的微分用 $ \dot{} $表示
$ \dot{\upsilon} = \upsilon^{\prime} \frac{ds}{dt} $
$ \ddot{\upsilon} = \upsilon^{\prime \prime} (\frac{ds}{dt})^{2} + \upsilon^{\prime} \frac{d^{2}s}{dt^{2}} $
$ \dddot{\upsilon} = \upsilon^{\prime \prime \prime} (\frac{ds}{dt})^{3} + 3 \upsilon^{\prime \prime} \frac{ds}{dt} \frac{d^{2}s}{dt^{2}} + \upsilon^{\prime} \frac{d^{3}s}{dt^{3}} $
$ \upsilon^{\prime}, \upsilon{\prime \prime} $互相垂直,上面第二式 $ \ddot{\upsilon} $是两个互相垂直的向量的分解的和。$ \upsilon^{\prime} \frac{d^{2}s}{dt^{2}} $这部分,和C的切线平行,它的大小为 $ \frac{d^{2}s}{dt^{2}} $( $ | \upsilon^{\prime} | = 1 $),另一部分 $ \upsilon^{\prime \prime}(\frac{ds}{dt})^{2} $,与C的主法线平行,大小为 $ \frac{1}{\rho} (\frac{ds}{dt})^{2} $($ | \upsilon^{\prime \prime} | = \frac{1}{\rho} $)。t为时间,加速度 $ \ddot{\upsilon} $这样的两成分分解得
$ | \ddot{\upsilon} |^{2} = \ddot{x}^{2} + \ddot{y}^{2} + \ddot{z}^{2} = \frac{1}{\rho} (\frac{ds}{dt})^{4} + (\frac{d^{2}s}{dt^{2}})^{2} $
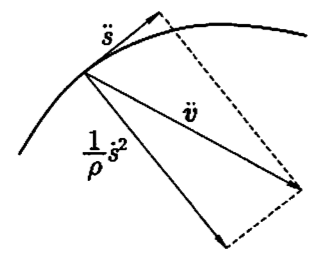
$ (\frac{ds}{dt})^{2} = \dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2} $微分得
$ \frac{ds}{dt} \frac{d^{2}s}{dt^{2}} = \dot{x}\ddot{x} + \dot{y}\ddot{y} + \dot{z}\ddot{z} $
从而
$ \begin{aligned} \frac{1}{\rho^{2}} (\frac{ds}{dt})^{6} = | \ddot{\upsilon} |^{2} (\frac{ds}{dt})^{2} - (\frac{ds}{dt})^{2} (\frac{d^{2}s}{dt^{2}})^{2} &= (\dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2})(\ddot{x}^{2} + \ddot{y}^{2} + \ddot{z}^{2}) - (\dot{x} \ddot{x} + \dot{y}\ddot{y} + \dot{z}\ddot{z})^{2} \\ &= \left | \begin{array}{cc} \dot{y} & \dot{z} \\ \ddot{y} & \ddot{z} \end{array} \right |^{2} + \left | \begin{array}{cc} \dot{z} & \dot{x} \\ \ddot{z} & \ddot{x} \end{array} \right |^{2} + \left | \begin{array}{cc} \dot{x} & \dot{y} \\ \ddot{x} & \ddot{y} \end{array} \right |^{2} \end{aligned} $
则
$ \frac{1}{\rho} = \frac{| \dot{\upsilon} \times \ddot{\upsilon} |}{| \dot{\upsilon} |^{3}} $
由
$ (\dot{\upsilon}, \ddot{\upsilon}, \dddot{\upsilon}) = (\frac{ds}{dt})^{6}(\upsilon^{\prime}, \upsilon^{\prime \prime}, \upsilon^{\prime \prime \prime}) $
有
$ \frac{1}{\tau} = \frac{(\dot{\upsilon}, \ddot{\upsilon}, \dddot{\upsilon})}{| \dot{\upsilon} \times \ddot{\upsilon} |^{2}} $
例子 螺旋线
$ x = a \cos{t}, \qquad y = a\sin{t}, \qquad z = ht \qquad (a > 0) $
$ \dot{x} = -a \sin{t}, \qquad \dot{y} = a \cos{t}, \qquad \dot{z} = h $
$ \ddot{x} = -a \cos{t}, \qquad \ddot{y} - -a \sin{t}, \qquad \ddot{z} = 0 $
$ \dddot{x} = a \sin{t}, \qquad \dddot{y} = -a \cos{t}, \qquad \dddot{z} = 0 $
$ | \dot{\upsilon} | = \sqrt{\dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2}} = \sqrt{a^{2} + h^{2}} $
$ | \dot{\upsilon} \times \ddot{\upsilon} | = \sqrt{a^{2}h^{2} \sin^{2}{t} + a^{2}h^{2} \cos^{2}{t} + a^{4}} = a \sqrt{a^{2} + h^{2}} $
$ (\dot{\upsilon}, \ddot{\upsilon}, \dddot{\upsilon}) = a^{2}h $
$ \frac{1}{\rho} = \frac{a}{a^{2} + h^{2}}, \qquad \frac{1}{\tau} = \frac{h}{a^{2} + h^{2}} $
即曲率和扭率是一定的,$ \tau, h $同符号,正负号区分右旋螺纹和左旋螺纹
平面曲线z = 0时,泰勒展开取二次项
$ \delta \upsilon = \upsilon^{\prime} \delta s + \upsilon^{\prime \prime} \frac{\delta s^{2}}{2} + o \delta s^{2} $
这时 $ | \upsilon^{\prime} | = 1 $,从而 $ \theta $是x轴的正方向,切线的正方向的角
$ | \upsilon^{\prime \prime} = | \frac{d \theta}{ds} | $
弧长s对应切线方向的变动率,即曲率
$ \frac{1}{\rho} = \frac{d \theta}{ds} $
$ \rho $为曲率半径,然而
$ \upsilon^{\prime} = (x^{\prime}, y^{\prime}) = (\cos{\theta}, \sin{\theta}) $
微分s得
$ \upsilon^{\prime \prime} = (x^{\prime \prime}, y^{\prime \prime}) = (- \sin{\theta \frac{d \theta}{ds}}, \cos{\theta \frac{d \theta}{ds}}) = \frac{1}{\rho} (- \sin{\theta}, \cos{\theta}) = \frac{1}{\rho} (-y^{\prime}, x^{\prime}) $
从
$ \frac{1}{\rho} = \frac{- x^{\prime \prime}}{y^{\prime}} = \frac{y^{\prime \prime}}{x^{\prime}} $
用一般的变量t表示为
$ \left | \begin{array}{cc} \dot{x} & \dot{y} \\ \ddot{x} & \ddot{y} \end{array} \right | = \left | \begin{array}{cc} x^{\prime} & y^{\prime} \\ x^{\prime \prime} & y^{\prime \prime} \end{array} \right | (\frac{ds}{dt})^{3} = \left | \begin{array}{cc} x^{\prime} & y^{\prime} \\ - \frac{y^{\prime}}{\rho} & \frac{x^{\prime}}{\rho} \end{array} \right | (\frac{ds}{dt})^{3} = \frac{1}{\rho} (\frac{ds}{dt})^{3} $
从而
$ \frac{1}{\rho} = \frac{\dot{x}\ddot{y} - \ddot{x}\dot{y}}{\dot{s}^{3}} $
用之前的记号
$ \frac{1}{\rho} = \frac{(\dot{\upsilon}, \ddot{\upsilon})}{| \dot{\upsilon} |^{3}} $
总之,用独立变量无关的微分记号得
$ \frac{1}{\rho} = \frac{dxd^{2}y - d^{2}xdy}{(dx^{2}+dy^{2})^{\frac{3}{2}}} $
特别地曲线为y = f(x),有
$ \frac{1}{\rho} = \frac{\frac{d^{2}y}{dx^{2}}}{(1 + (\frac{dy}{dx})^{2})^{\frac{3}{2}}} $
点P与曲线C相交,与C相对于切线在同一侧,半径等于 $ | \rho | $的圆为曲率圆,其中心 $ (\xi, \eta) $为曲率的中心
$ \xi = x - \rho \sin{\theta}, \qquad \eta = y + \rho \cos{\theta} $
如果$ \rho $和 $ \frac{d^{2}y}{dx^{2}} $同符号,下图右图曲率中心在曲线的凹侧
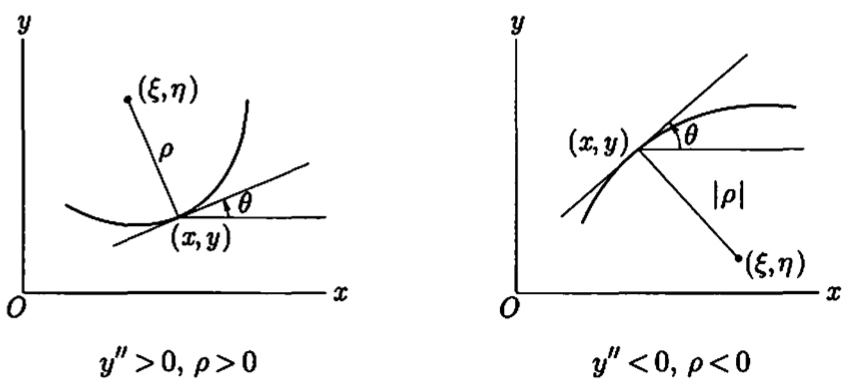
曲线C的曲率中心 $ (\xi, \eta) $的轨迹是曲线E的话,特别地C的弧长s作为变量,E为
$ \xi = x - \rho y^{\prime}, \qquad \eta = y + \rho x^{\prime} $
对s的微分的话
$ \xi^{\prime} = x^{\prime} - \rho^{\prime}y^{\prime} - \rho y^{\prime \prime} = - \rho^{\prime}y^{\prime} $
$ \eta^{\prime} = y^{\prime} + \rho^{\prime}x^{\prime} + \rho x^{\prime \prime} = \rho^{\prime}x^{\prime} $
从而
$ \xi^{\prime} x^{\prime} + \eta^{\prime}y^{\prime} = 0 $
即源曲线C的切线,和对应的点的E的切线互相垂直。则C的法线与E的曲率中心相接,E为源曲线C的法线的包络线
现在E的弧长为 $ \sigma $的话
$ (\frac{d \sigma}{ds})^{2} = (\frac{d \xi}{ds})^{2} + (\frac{d \eta}{ds})^{2} = \rho^{\prime 2} (x^{\prime 2} + y^{\prime 2}) = \rho^{\prime 2} $
即 $ \sigma^{\prime} = \pm \rho^{\prime} $。则在适当的方向上测量E的弧长,在 $ \rho^{\prime} \ne 0 $的各范围内,$ \sigma^{\prime} = \rho^{\prime} $,$ \sigma_ {0} $对应 $ \rho_ {0} $,有 $ \sigma - \sigma_ {0} = \rho - \rho_ {0} $。这样的条件下,E的两点间弧长对应C的亮点曲率半径的差
如果在E上缠绕一根线,在拉紧的同时松开P端,使线不下垂,P将画出C。因此,C是E的渐开线。反之,E是C的闭合线。C给定的时候,其渐开线E是固定的,但给定的渐开线E其C有无穷个
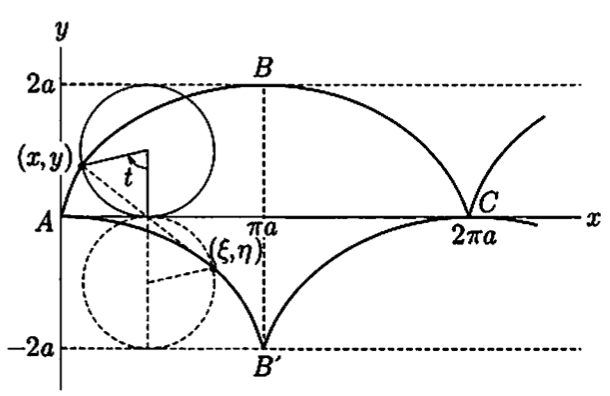
例子 当一个圆在另一个圆的圆周上或直线上滚动而不滑动,粘在运动圆上的一点的轨道是广义上称为摆线的曲线。最简单的应用是圆周上一点画的曲线为一个在恒定直线上滚动的圆,这是一条法线(狭义的)摆线(所谓的抓线)。如果半径为a,旋转角度为t,则直线为x轴,t = 0处圆圆周上的不动点P为坐标原点,抓线表示如下,以t作为变量
$ x = a(t - \sin{t}), \qquad y = a(1 - \cos{t}) $
则
$ dx = a(1 - \cos{t})dt, \qquad dy = a \sin{t}dt $
$ ds = \sqrt{dx^{2} + dy^{2}} = \sqrt{2a^{2}(1 - \cos{t})}dt = 2a | \sin{\frac{t}{2}} | dt $
$ d^{2}x = a \sin{t}dt^{2}, \qquad d^{2}y = a \cos{t}dt^{2} $
$ dxd^{2}y - dyd^{2}x = a^{2} \left | \begin{array}{cc} 1 - \cos{t} & \sin{t} \\ \sin{t} & \cos{t} \end{array} \right | dt^{3} = a^{2} (\cos{t} - 1)dt^{3} = -2a^{2} \sin^{2}{\frac{t}{2}} dt^{3} $
$ \rho = \frac{ds^{3}}{dxd^{2}y - dyd^{2}x} = -4a | \sin{\frac{t}{2}} | $
$ \xi = x - \rho \frac{dy}{ds} = a(t+ \sin{t}) $
$ \eta = y + \rho \frac{dx}{ds} = a(-1 + \cos{t}) $
因此闭合线和原曲线全等,具体来说,闭合线的弧 $ AB^{\prime}, B^{\prime}C $和原曲线的弧BC, AB全等。$ t = 0, t = \pi $对应 $ \rho = 0, \rho = -4a $,弧 $ AB^{\prime} $ 长为4a,从而摆线ABC的全长为8a
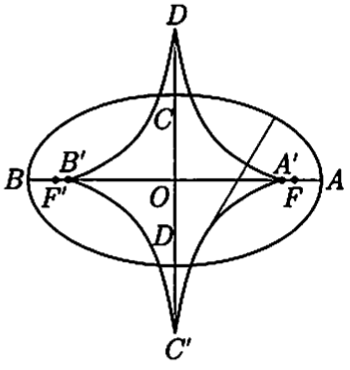
例子 椭圆的闭合线。椭圆
$ x = a \cos{t}, \qquad y = b \sin{t} $
其计算
$ \rho = \frac{(a^{2} \sin^{2}{t} + b^{2} \cos^{2}{t})^{\frac{3}{2}}}{ab} $
$ \xi = \frac{a^{2} - b^{2}}{a} \cos^{3}{t}, \qquad \eta = - \frac{a^{2} - b^{2}}{b} \sin^{3}{t} $
消掉t的闭合线方程式为
$ (a \xi)^{\frac{2}{3}} + (b \eta)^{\frac{2}{3}} = (a^{2} - b^{2})^{\frac{2}{3}} $
如下图中星形。原曲线曲率的极大极小点为闭合线的尖点
椭圆的四个法线是从E里面的点画的,两条法线是从E外面的点画的
例子 圆的渐开线,半径为1
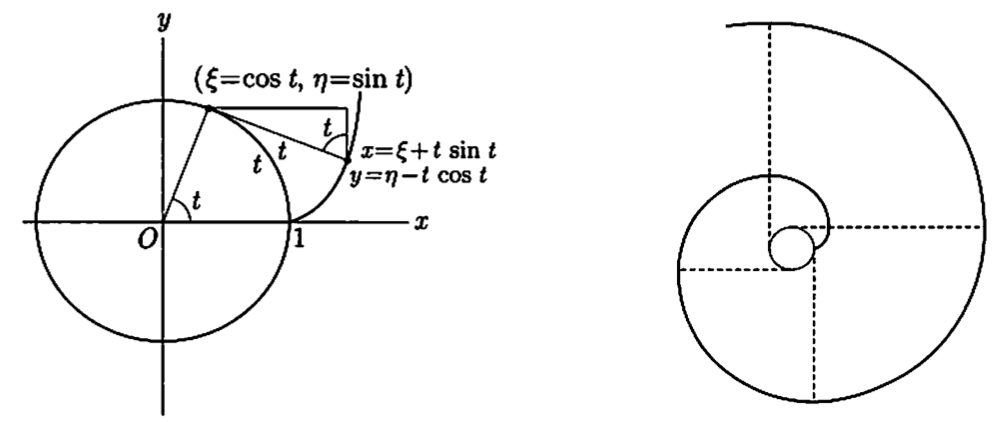
$ \xi = \cos{t}, \qquad \eta = \sin{t} $
则渐开线为
$ x = \cos{t} + t \sin{t}, \qquad y = \sin{t} - t \cos{t} $