Table of Contents
Parity arguments
让我们画一个大三角形,顶点为 $ A_ {1}, A_ {2}, A_ {3} $。我们分割它为任意有限个小三角形,如下图:
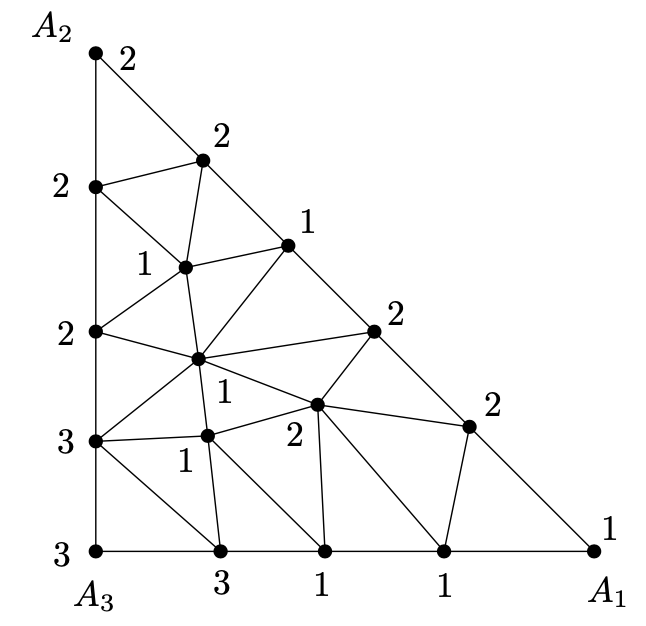
其中每个三角形都不会在其他三角形的边的里面,这样如果我们考虑该结果图为一个planar图形的绘制,所有内部的面都是三角形。让我们给大三角形和小三角形的顶点标签为1、2、3,在如下规则中:给顶点 $ A_ {i} $一个标签i,i = 1,2,3,且所有在边 $ A_ {i} A_ {j} $上的大三角形的顶点只能给标签为i或j,其他的顶点则可任意赋值
命题(Sperner引理 - planar版本)
在如上的描述中,一个顶点被赋值为1、2、3的小三角形总是存在
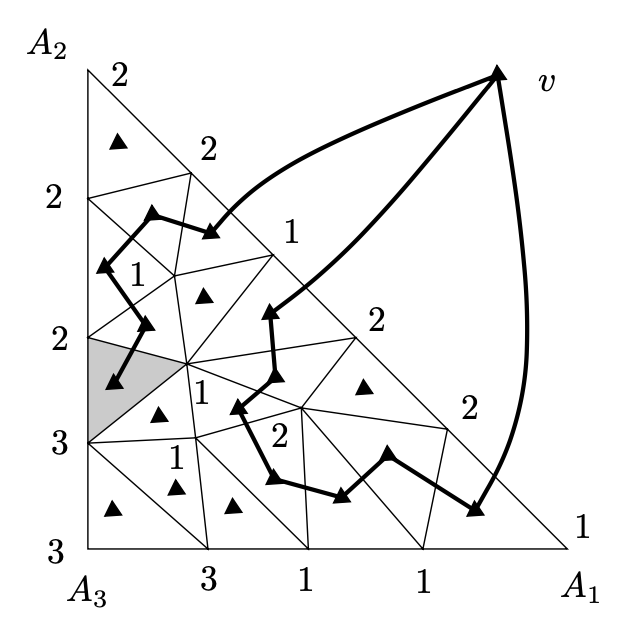
证明 我们定义一个辅助图形G;如上图。它的顶点为我们三角度量的面,例如,所有小三角形加上外层的面。在图中,顶点被描述为对应面中的小黑三角形。外层的面的顶点被记为v。两个顶点,例如,原始图形的面,由G的一条边连接如果有相邻的面且它们共同的边的端点标签为1和2。也考虑最外层面的顶点v,它连接所有小三角形邻接大三角周边边标签为12
一个小三角形在这个图形G中可连接一些它的邻居只在它的顶点标签为1且另一个标签为2。如果仍然有顶点标签为1或2,考虑的小三角形邻接两个邻居。如果仍然有顶点标签为3,则考虑三角形邻接一个邻居,且唯一的情况是图形G中小三角形的度数是奇数。我们现在显示顶点v(外层的面)在G中有奇数的度数。然后,通过握手引理,在G中存在至少另一个奇数度数的顶点,且这是想要的小三角形标签为1,2,3
图形G的边邻接v明显只与大三角形的边 $ A_ {1} A_ {2} $交叉。通过标签规则,该边只包含标签为1或2的顶点。让我们写下这些标签序列,开始于 $ A_ {1} $,结束于 $ A_ {2} $。v的邻居的数量是在这个序列中交替的1和2。因为序列开始于1结束于2,这样交替的数必须为奇数。因此v在G中是奇数的度数
命题(一维固定点定理)
对任意连续函数 $ f: [0, 1] \to [0, 1] $,存在一个点 $ x \in [0, 1] $使得f(x) = x
这样的x被称为函数f的固定点。该命题可通过考虑函数g(x) = f(x) - x来证明。这是一个连续函数其 $ g(0) \ge 0 $且 $ g(1) \le 0 $。直观上非常明显这样的连续函数的图形不能跳过x轴且因此g在[0,1]之间的某个点是0
固定点理论一般描述如下,在某种环境下,某些函数f必须有一个固定点,例如,存在一个x使得f(x) = x。这样的定理在数学的许多领域都是重要的结果。通常作为工具证明各种类型等式(积分、微分等)的存在方案
在Brouwer的固定点定理中,命题的一维间隔被平面的三角形替代,或三维空间中的四面体,或更高维的类似物。这里我们只证明2维空间版本因为我们只证明了2维的Sperner引理。
设 $ \Delta $记为平面上的一个三角形。为简化,让我们记三角形的顶点为 $ A_ {1} = (1, 0), A_ {2} = (0, 1), A_ {3} = (0, 0) $:
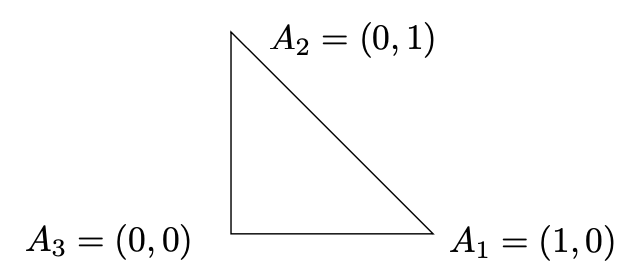
一个函数 $ f: \Delta \to \Delta $被称为连续的如果对 $ \forall a \in \Delta $且 $ \forall \epsilon > 0 $存在 $ \delta > 0 $使得如果 $ b \in \Delta $是从a开始距离最大为 $ \delta $的一个点则f(a)和f(b)的距离最多为 $ \epsilon $
定理(Planar Brouwer的固定点定理)
每个连续函数 $ f: \Delta \to \Delta $有一个固定点
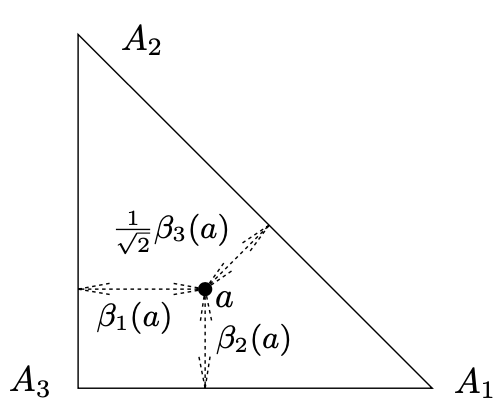
证明:我们定义三个辅助实值函数 $ \beta_ {1}, \beta_ {2}, \beta_ {3} $在三角形 $ \Delta $上。对一个在坐标(x, y)上的点 $ a \in \Delta $,我们设置
$ \beta_ {1}(a) = x, \quad \beta_ {2}(a) = y, \quad \beta_ {3}(a) = 1 - x - y $
地理上,$ \beta_ {i} $如下显示:
我们定义集合 $ M_ {1}, M_ {2}, M_ {3} \subseteq \Delta $:
$ M_ {i} = \{ a \in \Delta: \beta_ {i}(a) \ge \beta_ {i}(f(a)) \} $
i = 1, 2, 3。这样,$ M_ {i} $包含点通过函数f远离 $ A_ {i} $的相反面
注意每个点 $ p \in M_ {1} \cap M_ {2} \cap M_ {3} $是函数f的固定点,对如果p不是固定的则f必须移动离开某个面。更具体地,如果 $ p \in M_ {1} \cap M_ {2} \cap M_ {3} $则我们有 $ \forall i = 1, 2, 3, \beta_ {i}(p) \ge \beta_ {i}(f(p)) $且因为 $ \sum_ {i}\beta_ {i}(p) = \sum_ {i}\beta_ {i}(f(p)) = 1 $我们得到 $ \forall i, \beta_ {i}(p) = \beta_ {i}(f(p)) $,意味着p = f(p)。我们的目标现在是找到一个点在 $ M_ {1} \cap M_ {2} \cap M_ {3} $中
考虑一个序列三角化三角形$ \Delta $:
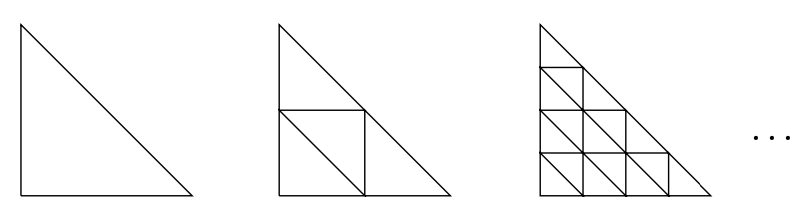
在每个这样的三角化中,我们标签三角形的所有顶点为1, 2和3。我们需要一个顶点标签i属于集合 $ M_ {i} $,且赋值满足Sperner引理规则。我们不得不确保这总是被排列的
顶点 $ A_ {1} $有从它的对边最大可能的距离;因此该距离在f下不会增加。因此 $ A_ {1} \in M_ {1} $且我们可标签 $ A_ {1} $为1;$ A_ {2}, A_ {3} $相似。一个点a在边 $ A_ {2}A_ {3} $上有 $ \beta_ {1}(a) + \beta_ {2}(a) = 1 $,意味着f(a)不能同时满足 $ \beta_ {1}(f(a)) > \beta_ {1}(a) $且 $ \beta_ {2}(f(a)) > \beta_ {2}(a) $。这样 $ a \in M_ {1} \cup M_ {2} $,且这样我们可在边 $ A_ {1}A_ {2} $上标签所有的顶点为1和2。其他边情况相似。最终,$ \Delta $的每个点属于至少一个 $ M_ {i} $集合因为它从所有边上都不能移动更远
Sperner引理意味着每个成功地提炼三角化有一个三角形标签为1,2,3。让我们记一些这样的三角形的顶点在第j次三角化中为 $ a_ {j,1}, a_ {j, 2}, a_ {j, 3}, a_ {j, i} \in M_ {i}, i = 1, 2, 3 $
考虑无穷序列点 $ (a_ {1,1}, a_ {2, 1}, a_ {3,1}, \ldots ) $。我们需要选择一个无穷收敛子序列。这总是可能的,事实上,在三角形内点的任意无穷序列包含一个收敛的无穷子序列。(三角形的该属性,例如,对任意闭合且有界平面的子集,被称为紧性)这样假设我们已经选择一个收敛的子序列$ (a_ {j_ {1}, 1}, a_ {j_ {2}, 1}, a_ {j_ {3}, 1}, \ldots), j_ {1} < j_ {2} < j_ {3} < \ldots $,且让我们记它的极限点为p
我们声称 $ p \in M_ {1} $。通过 $ M_ {1} $的定义,我们有 $ \beta_ {1}(a_ {j_ {k}}, 1) \ge \beta_ {1}(f(a_ {j_ {k}}, 1)), \forall j_ {k} $,且在两边使用一个极限有 $ \beta_ {1}(p) \ge \beta_ {1}(f(p)) $,因为使用极限在连续函数中会保留非严格不等式
因为三角形的直径在连续三角化中趋于0,其他顶点的序列,例如,$ (a_ {j_ {1}, 2}, a_ {j_ {2}, 2}, a_ {j_ {3}, 3}, \ldots) $和 $ (a_ {j_ {1}, 3}, a_ {j_ {2}, 3}, a_ {j_ {3}, 3}, \ldots) $,也收敛到点p。这意味着 $ p \in M_ {2} $且 $ p \in M_ {3} $。这样,p就是函数f想要的固定点
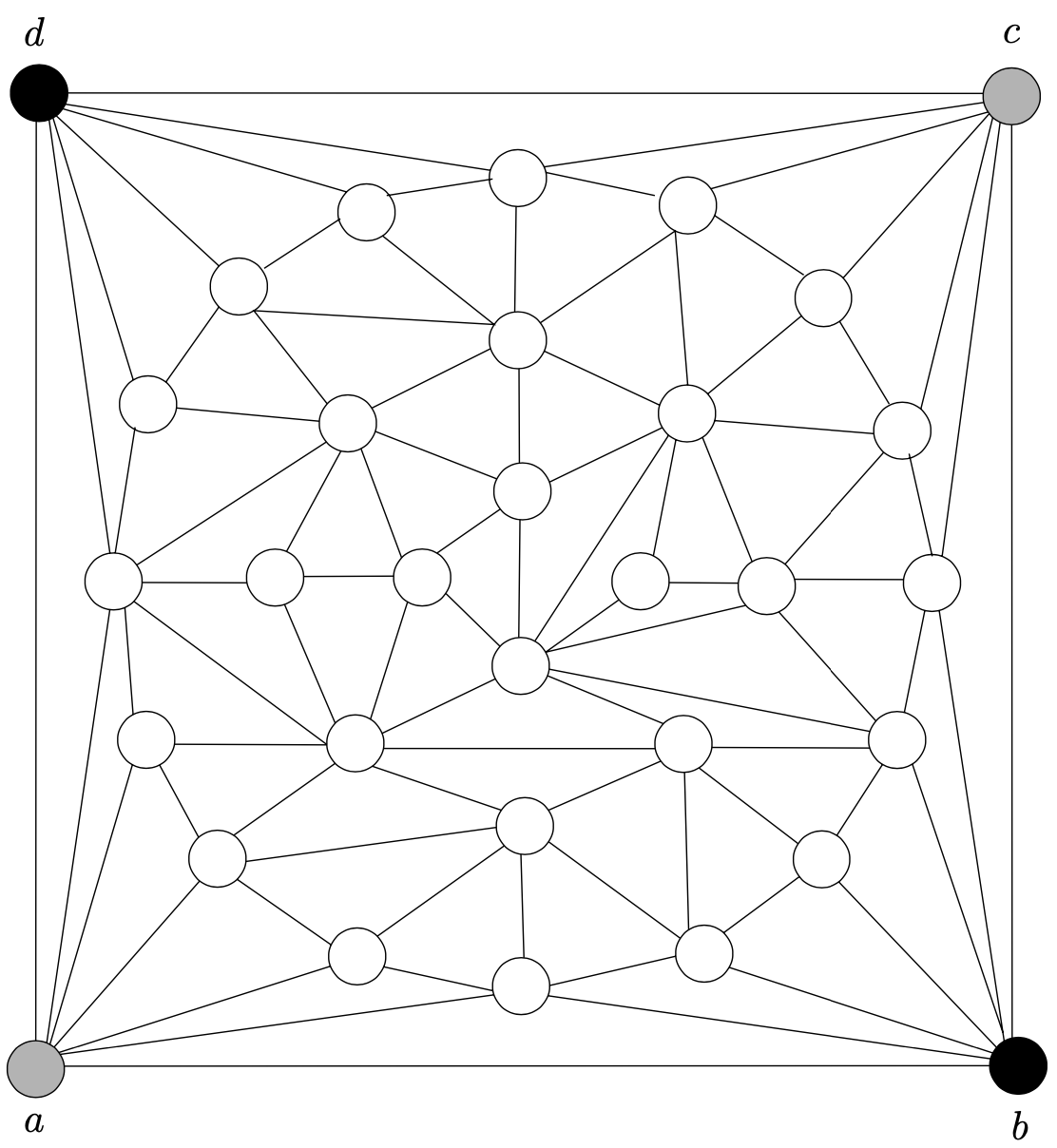
让我们展示另一个例子使用握手引理。我们将分析一个游戏。如上图,每个选手每次标注一个未标注节点,例如,第一个选手(Alice)标注为灰色,第二个选手(Betty)标注为黑色。在开始时,Alice有a、c两个标注节点,Betty有b、d标注节点。如果Alice能够标注从a到c的一条路径上所有节点则她获胜,Betty标注一条从b到d的路径上所有节点则他胜。如果节点都已标记完则为平局
命题
一个给定白板上(外层面是一个四方形,所有内部面是三角形),不存在有一个绘制
证明:假设存在一个绘制。让A为Alice标注的节点集合且设B为Betty标注的集合
让我们根据如下规则赋值标签1,2,3。如果一个A中节点可通过一个所有顶点属于A的路径连接到a则标记为1,相似地,如果B中节点能通过一个所有顶点为B中节点的路径连接到b则标签为2。剩下的节点标记为3。通过假设,c和d都标记为3,否则有一个选手已经胜利了
我们将显示有一个内部三角面T标签为1,2,3。这导致一个矛盾,因为标签为3的T的节点(称为x)不能属于A或B。如果x属于A,我们考虑三角形T中节点y标签为1。通过标签的定义,存在一个从a到y的路径只使用A中节点,且这个路径可扩展到x,因为y邻接x。相似地我们可得出x不属于B,这是一个矛盾。原因如下图:
Sperner’s theorem on independent systems
定理(Sperner定理)
任意n个元素集合的独立系统的子集包含最多 $ {n \choose \lfloor \frac{n}{2} \rfloor} $个集合
这事实上是一个偏序集的定理。考虑 $ 2^{X} $的集合系统包含集合X的所有子集。考虑集合系统 $ 2^{X} $包含所有X集合的子集合。关系 $ \subseteq $,“子集“,是在$ 2^{X} $上的一个偏序(它甚至是偏序的一个最重要的例子)。集合的独立系统是偏序集 $ (2^{X}, \subseteq) $ 中一对不可比较元素的集合。偏序集中不可比较元素对的集合被称为antichain,这样Sperner定理对任意 $ (2^{X}, \subseteq) $里的antichain的大小给定了一个上界
在我们开始证明Sperner定理之前,我们应该标记该理论的上限是最大可能性,因为大小为 $ \lfloor \frac{n}{2} \rfloor $的X的所有子集组成大小为 $ {n \choose \lfloor \frac{n}{2} \rfloor } $的一个独立系统
证明 我们首先说X的子集的chain是X的子集的任意集合 $ \{A_ {1}, A_ {2}, \ldots, A_ {k} \} $ 使得 $ A_ {1} \subset A_ {2} \subset \cdots \subset A_ {k} $。在有序集语言中,它是简单的偏序集 $ (2^{X}, \subseteq) $的线性有序子集
一个关键的观察是在任意antichain中任意chain最多有一个共同元素。例如,如果我们成功证明问题中整个偏序集可被表达为最多r个chains的集合,则没有antichain有超过r个元素。我们的证明使用这个简单的观察在更复杂的情况中
我们考虑 $ (2^{X}, \subseteq) $中的最大chains,最大chain是如果我们添加它到 $ 2^{X} $中的任意其他集合,结果都不是一个chain。它容易看到最大chain如下:它们包含X的每个可能大小的子集;即,他们有形如:
$ \begin{equation} \emptyset \subset \{x_ {1} \} \subset \{x_ {1}, x_ {2}\} \subset \{x_ {1}, x_ {2}, x_ {3}\} \subset \cdots \subset \{ x_ {1}, x_ {2}, \ldots, x_ {n} \} \end{equation} $
$ x_ {1}, x_ {2}, \ldots, x_ {n} $是X中以某个顺序排列的所有元素。每个最大chain因此导入X的一个线性有序元素,另一方面,每个线性有序会有一个最大chain。结果,最大chain的数目等于X的排列的数目,为n!
设 $ \mathcal{M} $为一个antichain(子集的独立系统),形成所有有序对 $ (\mathcal{R}, M), M \in \mathcal{M} $是一个集合且 $ \mathcal{R} $是包含M的最大chain。我们以两种方法统计该元组
首先,通过上述观察到,每个chain包含最多一个 $ M \in \mathcal{M} $(因为 $ \mathcal{M} $是一个antichain),这样元组 $ (\mathcal{R}, M) $的数量小于等于最大chain的数量,为n!
另一方面,我们可用一个集合 $ M \in \mathcal{M} $且问多少最大chain包含它。一个最大chain包含M当且仅当 $ \{x_ {1}, x_ {2}, \ldots, x_ {k} \} = M, k = | M | $。因此我们问多少个X的线性有序使得前k个元素为M的元素。我们排序M的元素有k!种方法,这样确定前面k个chain的子集,且M外的元素可有 $ (n - k)! $种排序方法,这确定了chain剩下的元素。这样包含M的最大chain有 $ k! (n-k)! $个。这样有序对 $ (\mathcal{R}, M) $的数量等于
$ \sum_ {M \in \mathcal{M}} | M | ! (n - | M |)! $
根据第一种统计方法,有n!个,这样我们获得
$ \begin{equation} \sum_ {M \in \mathcal{M}} \frac{| M | ! (n - | M |)!}{n!} = \sum_ {M \in \mathcal{M}} \frac{1}{\left( \begin{array}{c} n \\ | M | \end{array} \right)} \le 1 \end{equation} $
我们使用这个事实 $ \left(\begin{array}{c} n \\ \lfloor n / 2 \rfloor \end{array} \right) $是至少最大的形如 $ { n \choose k } $的任意二项式系数,$ k = 0, 1, \ldots, n $。因此
$ 1 \ge \sum_ {M \in \mathcal{M}} \frac{1}{ \left(\begin{array}{c}n \\ \lfloor n / 2 \rfloor \end{array}\right)} \ge | \mathcal{M} | \frac{1}{\left(\begin{array}{c} n \\ \lfloor n / 2 \rfloor \end{array}\right)} $
因此 $ | \mathcal{M} | \leq \left(\begin{array}{c}n \\ \lfloor n / 2\rfloor\end{array}\right) $
Sperner定理的其他证明 和许多其他定理一样,Sperner定理可用不同的方法证明。我们将描述另两种证明方法。首先是用特殊的chain覆盖 $ 2^{X} $
让我们考虑偏序集 $ (2^{X}, \subseteq) $中的chain,例如,包含关系的集合序列:$ M_ {1} \subset M_ {2} \subset \cdots \subset M_ {t} $。称这样的一个chain是对称的如果它包含一个大小为k的集合,一个大小为k+1的集合,一个大小为k+2的集合,…,一个大小为n-k的集合,且没有其他集合。例如,对n = 3,chain包含集合{2} 和{2,3}是对称的,chain $ \{ \emptyset, \{3\}, \{2,3\}, \{1,2,3\} \} $也是对称的,但chain $ \{ \{ 1 \} \} $和 $ \{ \emptyset, \{1,2,3\} \} $不是对称的。对称chain的一部分是表达 $ 2^{X} $作为几个不相交对称chain的联合
任何部分称为对称chain(如果它存在)可以组成 $ \left( \begin{array}{c} n \\ \lfloor n / 2 \rfloor \end{array} \right) $个对称chain,因为每个对称chain包含一个大小为 $ \lfloor n / 2 \rfloor $的集合。每个chain有最多一个共同的任意独立集合系统的集合(这基于Sperner定理第一个证明的观察)。因此Sperner定理有如下结论:
声明 对任意有限集合X,系统 $ 2^{X} $有一个部分为对称chain
证明:我们可假设 $ X = \{1,2,\ldots,n \} $。证明基于如下构建:
对每个集合 $ M \subseteq X $,我们赋值一个序列 “$ m_ {1}m_ {2} \ldots m_ {n} $”包含左右括号
$ m_{i}=\left\{\begin{array}{ll}”(“ & \text { if } i \in M \\ “) “ & \text { if } i \notin M\end{array}\right. $
例如,对n = 7和集合 $ M = \{2,6\} $,我们有序列 $ “m_ {1}m_ {2}\ldots m_ {7}” = “)()))()” $。该序列左右括号不需要匹配上。首先,我们配对所有临近的括号,然后我们忽略已经配对的括号,且根据相同的规则配对剩下的括号。这里有两个例子:
$ ) \underbrace{()})) \underbrace{()} $
$ )))(\underbrace{(\underbrace{()}\underbrace{()})} ( $
在完成配对过程后,一些括号可能依然没有匹配上。我们说两个括号序列有相同的部分配对如果配对括号相同。如下面的例子:
$ M_ {1} = \{4,5,6,8,11\} \qquad \ldots \qquad )))((()())( $
$ M_ {2} = \{5,6,8,11\} \qquad \ldots \qquad ))))(()())( $
$ M_ {3} = \{5,6,8\} \qquad \ldots \qquad ))))(()())) $
我们现在定义一个相等 $ \sim $在集合 $ 2^{X} $上,$ M \sim M^{\prime} $当且仅当M和 $ M^{\prime} $有相同的偏配对。我们声称这样序列的每个类是一个对称chain
最后我们显示另一个Sperner定理的证明。它明显不同于之前的两个证明,使用偏序集 $ (2^{X}, \subseteq) $的高对称结构
我们开始一个一般化定义。设 $ (X, \le) $和 $ (Y, \preceq) $为相同的偏序集。一个映射$ f: X \to Y $被称为偏序集的同构如果f是一个双射且对任意两个元素 $ x, y \in X, x \le y $成立当且仅当 $ f(x) \preceq f(y) $。一个偏序集 $ (X, \le) $映射到它自身的同构被称为$ (X, \le) $的自同构。一个自同构保留关系 $ \le $的所有属性。例如,x是某些子集 $ A \subseteq X $的最大元素当且仅当f(x)是集合f(A)的最大元素
Sperner定理的第三个证明 设X为一个给定的n元集合。每个排列 $ f: X \to X $引入一个映射 $ f^{\#} : 2^{X} \to 2^{X} $(例如,发送X的子集到X的子集)由 $ f^{\#}(A) = \{f(x): x \in A \} $。它明显 $ f^{\#} $是一个双射 $ 2^{X} \to 2^{X} $,且是偏序集 $ (2^{X}, \subseteq) $的一个子同构
让我们考虑集合X的子集的一个系统 $ \mathcal{M} $。对集合X的每个排列f,我们给定一个集合系统 $ \{ f^{\#}(M): M \in \mathcal{M} \} $;即在映射 $ f^{\#} $下 $ \mathcal{M} $的集合的像的系统。我们定义一个新的映射:
$ f^{\#\#} : 2^{2^{X}} \to 2^{2^{X}} $
(赋值集合系统到集合系统)通过公式
$ f^{\#\#}(\mathcal{M}) = \{ f^{\#}(M): M \in \mathcal{M} \} $
映射 $ f^{\#\#} $也是一个双射
我们引入一个关系 $ \vartriangleleft $在X的所有集合系统的集合上(例如,在集合 $ 2^{2^{X}} $:
$ \mathcal{M} \vartriangleleft \mathcal{N} \leftrightarrow \text{for each } M \in \mathcal{M} 有一个N \in \mathcal{N}使得 M \subseteq N $
注意关系 $ \vartriangleleft $是跟集合系统间的包含关系不同。它可能比包含( $ \mathcal{M} \subseteq \mathcal{N} $意味着 $ \mathcal{M} \vartriangleleft \mathcal{N} $)更大的关系。读者被邀请来检查关系 $ \vartriangleleft $是反射和转移的,但它不需要反对称
设字母 $ \Xi $代表在集合X上所有独立集合系统的集合( $ \Xi \subset 2^{2^{X}} $)。我们声称关系 $ \vartriangleleft $限制到 $ \Xi $是已经非对称的,且它是在 $ \Xi $的偏序。如果 $ \mathcal{M} $和 $ \mathcal{N} $为集合的独立系统使得 $ \mathcal{M} \vartriangleleft \mathcal{N} $和 $ \mathcal{N} \vartriangleleft \mathcal{M} $,我们考虑一个任意集合 $ M \in \mathcal{M} $。系统 $ \mathcal{N} $不得不包含一些集合 $ M^{\prime} \supseteq M $,且然后 $ \mathcal{M} $包含一些 $ M^{\prime \prime} \supseteq M^{\prime} $。这样我们获得 $ M, M^{\prime \prime} \in \mathcal{M}, M \subseteq M^{\prime \prime} $,且通过 $ \mathcal{M} $的独立有 $ M = M^{\prime \prime} = M^{\prime} $,因此 $ M \in \mathcal{N} $。这显示 $ \mathcal{M} \subseteq \mathcal{N} $,且对称的我们获得 $ \mathcal{N} \subseteq \mathcal{M} $,因此$ \mathcal{M} = \mathcal{N} $。这样 $ (\Xi, \vartriangleleft) $是一个有序集
进一步我们声称对任意排序f,映射 $ f^{\# \#} $是偏序集 $ (\Xi, \vartriangleleft) $的子同构
Sperner定理的证明基于如下引理:
引理 设 $ \Xi_ {0} \subseteq \Xi $记为带最大可能集合数的独立集合系统的集合。集合 $ \Xi_ {0} $有最大元素 $ \mathcal{N}_ {0} $,对应 $ \vartriangleleft $的顺序。这意味着 $ \forall \mathcal{M} \in \mathcal{M}, \mathcal{M} \vartriangleleft \mathcal{N}_ {0} $
引理的证明 因为X上只有有限的集合系统,它有效的证明对任意两个集合系统 $ \mathcal{M}, \mathcal{M}^{\prime} \in \Xi_ {0} $,存在一个集合系统 $ \mathcal{N} \in \Xi_ {0} $比 $ \mathcal{M}, \mathcal{M}^{\prime} $要大,例如,$ \mathcal{M} \vartriangleleft \mathcal{N}, \mathcal{M}^{\prime} \vartriangleleft \mathcal{N} $
这样我们考虑某个 $ \mathcal{M}, \mathcal{M}^{\prime} \in \Xi_ {0} $,且我们形成一个新的集合系统 $ \bar{\mathcal{M}} = \mathcal{M} \cup \mathcal{M}^{\prime} $。因为 $ \mathcal{M}, \mathcal{M}^{\prime} $是独立的,在 $ \bar{\mathcal{M}} $中的最长chain,包含 $ \bar{\mathcal{M}} $的顺序,有最多两个集合。接着,设 $ \bar{\mathcal{M}}_ {min} $为所有从 $ \bar{\mathcal{M}} $中的集合的系统,$ \bar{\mathcal{M}} $包含没有适合的子集合,或对于包含关系 $ \bar{\mathcal{M}} $最小的所有集合的系统。相似地我们引入系统 $ \bar{\mathcal{M}}_ {max} $作为所有包含最大集合 $ \bar{\mathcal{M}} $的系统。我们想要检查系统 $ \mathcal{N} = \bar{\mathcal{M}}_ {max} $属于 $ \Xi_ {0} $且满足 $ \mathcal{M} \vartriangleleft \bar{\mathcal{M}}_ {max}, \mathcal{M}^{\prime} \vartriangleleft \bar{\mathcal{M}}_ {max} $
系统 $ \bar{\mathcal{M}}_ {min}, \bar{\mathcal{M}}_ {max} $是独立的,且我们有 $ \bar{\mathcal{M}} = \bar{\mathcal{M}}_ {min} \cup \bar{\mathcal{M}}_ {max} $。明显地 $ \bar{\mathcal{M}}_ {max} \vartriangleleft \mathcal{M}, \bar{\mathcal{M}}_ {max} \vartriangleleft \mathcal{M}^{\prime} $。它仍然检测 $ \bar{\mathcal{M}}_ {max} $有集合最大可能数,例如,$ | \bar{\mathcal{M}}_ {max} | = | \mathcal{M} | $。让我们注意通过 $ \mathcal{M}, \mathcal{M}^{\prime} $的独立性,我们得到 $ \mathcal{M} \cap \mathcal{M}^{\prime} \subseteq \bar{\mathcal{M}}_ {min} \cap \bar{\mathcal{M}}_ {max} $。因此 $ | \bar{\mathcal{M}}_ {min} | + | \bar{\mathcal{M}}_ {max} | = | \bar{\mathcal{M}}_ {min} \cap \bar{\mathcal{M}}_ {max} | + | \bar{\mathcal{M}}_ {min} \cap \bar{\mathcal{M}}_ {max} | \ge | \mathcal{M} \cup \mathcal{M}^{\prime} | + | \mathcal{M} \cap \mathcal{M}^{\prime} | = | \mathcal{M} | + | \mathcal{M}^{\prime} | $, 且这样如果我们有 $ | \bar{\mathcal{M}}_ {max} | < | \mathcal{M} | = | \mathcal{M}^{\prime} | $则我们得到 $ | \mathcal{M}_ {min} | > | \mathcal{M} | $且系统 $ \mathcal{M}, \mathcal{M}^{\prime} $没有最大可能大小。这证明了引理
一个额外的问题:禁止4循环
在之前的章节我们调研n个顶点的图形最大可能的边数,且没有三角形的子图形。这里我们继续调研一个看着相似的问题:n个顶点图形的最大肯能边数,且不包含 $ K_ {2,2} $的同构子图形(即长度为4的循环)?一个子图形要考虑如下情况,例如,4个顶点的完全图 $ K_ {4} $包含一个 $ K_ {2,2} $
可能会认为禁止 $ K_ {2,2} $会跟禁止 $ K_ {3} $相似,但奇怪的是,答案是不同的。一个不包含三角形的图形最多有 $ \lfloor n^{2} / 4 \rfloor $条边,大约 $ {n \choose 2} $的一半,而禁止 $ K_ {2,2} $的最大变数更小,大约 $ n^{3 / 2} $
定理
如果一个n个顶点的图形G不包含 $ k_ {2,2} $的同构,它最多有 $ \frac{1}{2} (n^{3/2} + n) $个边
证明 我们将统计所有 $ ( \{ u, u^{\prime} \}, v) $对的集合M,$ v \in V, \{u, u^{\prime} \} \in {V \choose 2} $,且v跟u, $ u^{\prime} $有一条边相连。即如下图形式

对一个固定对 $ \{u, u^{\prime} \} $,只有一个顶点 $ v \in V $可能存在连接到u和 $ u^{\prime} $。如果有两个这样的顶点,v和 $ v^{\prime} $,它们将和u、$ u^{\prime} $形成一个 $ K_ {2,2} $的子图形同构。因此 $ | M | \le {n \choose 2} $
现在让我们看有多少形如 $ (\{u, u^{\prime}\}, v) $的元素被固定顶点 $ v \in V $贡献到集合M。对每对 $ \{u, u^{\prime} \} $的邻居,v贡献M的一个元素,这样如果v有d度它贡献 $ {d \choose 2} $个元素。因此,如果我们记 $ d_ {1}, d_ {2}, \ldots, d_ {n} $为V的顶点的度数,我们获得 $ | M | = \sum^{n}_ {i=1} {d_ {i} \choose 2} $
加上之前的估计,我们获得
$ \sum^{n}_ {i=1}{d_ {i} \choose 2} \le {n \choose 2} $
同时,图形边的数量为 $ \frac{1}{2} \sum^{n}_ {i=1} d_ {i} $。剩下的证明为一个不等式的乘积
命题(Cauchy-Schwarz不等式)
对任意实数 $ x_ {1}, x_ {2}, \ldots, x_ {n} $和 $ y_ {1}, y_ {2}, \ldots, y_ {n} $我们有
$ \sum^{n}_ {i=1} x_ {i}y_ {i} \le \sqrt{\sum^{n}_ {i=1}x^{2}_ {i}} \sqrt{\sum^{n}_ {i=1}y^{2}_ {i}} $
Cauchy-Schwarz不等式有一个漂亮的几何意义。如果我们解释 $ x = (x_ {1}, \ldots, x_ {n}) $ 和 $ y = (y_ {1}, \ldots, y_ {n}) $为n维欧几里得空间中的向量,不等式的左边是x和y的向量乘积,右边是向量长度的乘积。一个著名的向量公式为两个向量夹角的余弦等于它们的向量乘积除以它们长度的乘积。
第一个证明:AG不等式 让我们写 $ X = \sum^{n}_ {i=1}x^{2}_ {i} $ 和 $ Y = \sum^{n}_ {i=1}y^{2}_ {i} $。如果X = 0,则所有 $ x_ {i} $为0且不等式成立,Y = 0也类似。让我们现在假设X > 0 且 Y > 0,我们定义 $ a_ {i} = x^{2}_ {i} / X, b_ {i} = y^{2}_ {i} / Y $。算术和几何不等式告诉我们 $ \sqrt{a_ {i}b_ {i}} \le (a_ {i} + b_ {i}) / 2 $。通过不等式相加,我们获得左边为
$ \sum^{n}_ {i=1} \sqrt{a_ {i}b_ {i}} = \sum^{n}_ {i=1} \frac{| x_ {i} y_ {i} |}{\sqrt{XY}} $
而右边为
$ \frac{1}{2} \left(\frac{1}{X} \sum^{n}_ {i=1}x^{2}_ {i} + \frac{1}{Y} \sum^{n}_ {i=1}y^{2}_ {i} \right) = \frac{1}{2}(1 + 1) = 1 $
因此 $ \sum^{n}_ {i=1} \frac{| x_ {i}y_ {i} |}{\sqrt{XY}} \le 1 $,调整该式即可得Cauchy-Schwarz不等式
第二个证明:magic with a discriminant 我们固定数 $ x_ {i}, y_ {i} $,且我们定义一个新变量t的函数p:
$ p(t) = \sum^{n}_ {i=1}(x_ {i} + ty_{i})^{2} $
我们看到p(t)是一个二次方函数形如 $ p(t) = at^{2} + bt + c, a = \sum^{n}_ {i=1}y^{2}_ {i}, b = \sum^{n}_ {i=1}2x_ {i} y_ {i}, c = \sum^{n}_ {i=1}x^{2}_ {i} $,另一方面,p(t)是一个平方和,因此对所有实数t方程非负
如果二次等式 $ a t^{2} + bt + c = 0 $有一个正discriminant,则它有两个实数解,且这样函数p(t)在实数轴的部分有负值。因此,discriminant是非正的,例如,$ b^{2} - 4ac \le 0 $。因此可获得Cauchy-Schwarz不等式
结束定理7.3.1的证明 明显,我们可假设我们的图形没有孤立点,因此 $ \forall i, d_ {i} \ge 1 $。然后我们有 $ {d_ {i} \choose 2} \ge \frac{1}{2} (d_ {i} - 1)^{2} $,且我们获得
$ \sum^{n}_ {i=1} (d_ {i} - 1)^{2} \le n^{2} $
我们现在应用Cauchy-Schwarz不等式 $ x_ {i} = d_ {i} - 1, y_ {i} = 1 $,我们得到
$ \sum^{n}_ {i=1}(d_ {i} - 1) \le \sqrt{\sum^{n}_ {i=1}(d_ {i} - 1)^{2}} \sqrt{n} \le \sqrt{n^{2}} \sqrt{n} = n^{3/2} $
所以 $ | E(G) | = \frac{1}{2} \sum^{n}_ {i=1} d_ {i} \le \frac{1}{2} (n^{3/2} + n) $
意图 在证明中,我们导出了 $ \sum^{n}_ {i=1} {d_ {i} \choose 2} $的一个上界,且我们问 $ \sum^{n}_ {1}d_ {i} $多大。对不算小的 $ d_ {i} $,$ {d_ {i} \choose 2} $大约 $ \frac{1}{2}d^{2}_ {i} $。给定 $ \sum d^{2}_ {i} $大约 $ n^{2} $,使 $ \sum d_ {i} $最大的方法是选择所有的 $ d_ {i} $相等,在我们的例子中意味着每个都应该是 $ \sqrt{n} $。则 $ \sum d_ {i} $大约 $ n^{3/2} $。当然,这不是一个证明,但这样一个粗略的计算可经常给我们一个如何进行的好的想法