Table of Contents
Algorithm
Leetcode 354: https://leetcode.com/problems/russian-doll-envelopes/
https://dreamume.medium.com/leetcode-354-russian-doll-envelopes-1d11184d1cc
Review
Understanding the Limitations of Causally and Totally Ordered Communication
https://www.cs.rice.edu/~alc/comp520/papers/Cheriton_Skeen.pdf
摘要
关系和总序通讯支持(CATOCS)已被提议为构建可靠分布式系统的基础构建块的重要部分。在本文中,应用CATOCS到分布式应用程序的几种类型,且这些设施在通讯可扩展性和健壮性上潜在的影响。从这些调查研究中,我们发现CATOCS有限的价值和一些潜在的问题。CATOCS基本的困难是它尝试在通讯层解决状态问题违背了著名的端到端的争论
简介
关系和总序通讯支持(CATOCS)以被提议为构建可靠分布式系统的另一个重要基础设施。关系序通讯确保消息转发为一个和潜在的消息关系依赖一致的顺序,及在分布式系统中引入一个覆盖事件偏序的逻辑时钟模型。总序通讯支持进一步确保消息以相同的顺序转发给所有参与者。CATOCS实现也提供消息转发的原子性,确保要么所有消息转发要么不转,至少在进程上在兴趣间隔期间不会故障。CATOCS实现也提供故障通知,其在消息流通中为关系(或总)序。对这些设施,CATOCS已被支持作为解决一些重要的分布式计算问题,包含数据复制的良好工具
然而,CATOCS可只被视为确定一个重要的实际应用程序的一个类,其设施为有效且高效,且它的要求不能使用替代的、一般性的机制有效满足。在本文中,我们调研CATOCS对某些类型分布式应用程序的适用性,特别关注于使用CATOCS的例子中。从这些调研中,我们发现使用CATOCS有限的价值。CATOCS基本的困呢可被解释为端到端争议。CATOCS是在通讯层面,但一致性要求通常表达为应用程序状态
下一节描述关系和总序通讯支持(CATOCS)更多的细节。第3节描述在各种通讯场景中这些技术的一些重要限制和开销。第4节考虑关系和总序协议对一些分布式应用程序类型的适用性,包含使用CATOCS协议的例子。我们在第3节展示的限制在这些应用程序中使用CATOCS有重要的限制。第5节呈现争论为什么CATOCS在通讯数据传输路径上有显著的扩展开销。我们也包含了使用面向对象技术的一个状态层处理实现提供一个更有效、稳健、可扩展和容易指导出我们考虑的分布式系统问题的解决方案
关系和总序通讯
在关系顺序消息系统中,消息以消息发送的顺序转发,作为被发生之前关系来确定但限制消息发送和接收事件。为方便起见,我们扩展发送之前关系包括消息。在最简单的例子中,消息m1被称为发生在m2之前如果存在一个进程P比如m1在P进程被发送或接收在发送m2之前。这些简单例子的传输闭合汇成了消息的完全发生之前关系。术语causally precedes跟发生之前是一个意思,例如,m1 causally-precedes m2如果m1 发生在m2 之前
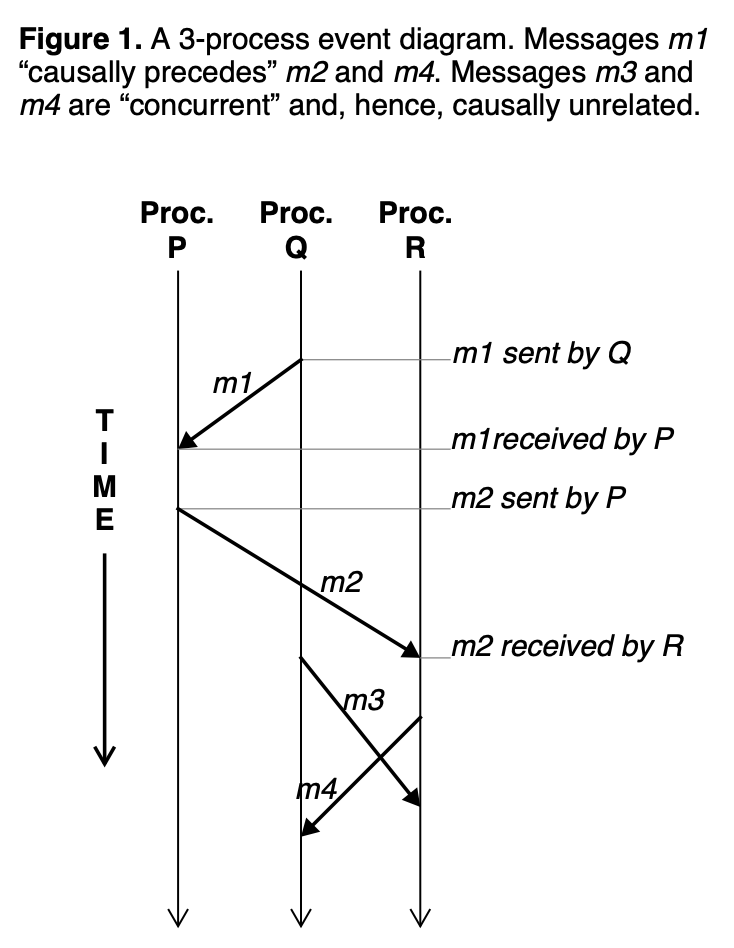
图1展示了关系序使用一个普通的事件图表。消息发送和接受事件按列排列,每个进程一个,时间是从上往下。图表显示进程Q发送m1,之后被进程P接收。然后P发送m2,被进程R接收。消息m1跟m2和m4有关系。消息m3和m4被称为并行因为它们之间没有关系
关系多播以发生之前关系转发消息到一个进程组。如果两个消息多播到相同的进程组且发送一个消息在另一个消息之前,则第一个消息转发到组中所有进程在后一个消息之前。因此,关系多播保留发生之前关系
总序多播在一个进程组中以相同的顺序转发所有消息到所有进程。消息转发通常根据发生之前关系,且我们作此假设,虽然一些系统不提供任何关系序保障
许多系统提供CATOCS也实现原子消息转发,确保一个消息转发到所有非故障进程。没有原子转发,在一个进程上消息丢失可能未定义的延迟所有关系依赖消息的接收,丢掉这些消息。一个消息的丢失可能强制任意数量的消息丢失。原子消息转发可以一个相对直接的方式实现,让组中每个进程缓存它接收到的每个消息直到它确保消息是温度的,例如,被所有组中其他成员接收到。因此,我们假设本讨论中CATCOS系统也提供原子消息转发。注意,然而,消息转发的原子属性不包括CATCOS多播执行过程中故障的进程。因此消息转发是原子的,但不是耐久的。(一个行为是耐久的如果它的改变存留在故障和恢复中)特别地,如果在CATOCS协议执行中消息温度前发送者故障,不保证剩下的工作进程接收和转发该消息。作为这个问题的一个特殊例子,一个进程可发送一个消息到它的进程组,接收且形如一个本地消息(作为一个成员)且然后故障,没有任何其他进程组成员接收该消息,可能导致它的状态跟进程组中其他成员不一致。CATOCS中原子耐久消息转发成本比较昂贵,在我们知晓的任意实现中都不支持,且还是使用CATOCS可靠复制数据更新的一个重大缺陷
CATOCS系统也提供故障通知,对组中每个进程有消息接收一样的一致顺序。注意顺序故障通知可在没有CATOCS的情况下提供且作为单独能力是有用的。然而,它应该被强调我们聚焦于理解消息转发顺序,因此,我们不考虑顺序故障通知作为一个独立的能力
有系统支持多播和进程组但不支持关系通讯,IP多播和早期V-System中的UDP即为两个例子。也有系统采用关系序和其他不兼容通讯系统的序关系,Munin是一个例子。我们的关心点是在通讯系统中从多个源的转发消息实现序关系
CATOCS提供的序在本文中被称为次要顺序,因为它基于一个进程组通讯的事件顺序。这种次要顺序通过消息中的信息决定的语义顺序是不需要一致性的。例如,一个数据库改变的通知应该被已提交到数据库系统的顺序广播,但CATOCS只确保这个语义顺序如果更新被提供给通讯系统作为事件发生的语义顺序。结果,许多系统使用或提供我们称为的规范顺序,其消息转发顺序有效地基于顺序限制在进程发送消息时直接指定或嘱咐的顺序。如下节所述,规范序使用state-level时钟,世俗的或逻辑的,在许多真实的应用程序中提供一个相比CATCOS有吸引力的替代方案
Tips
- 书中有代码讲解的地方还是看代码讲解比较容易理解,直接看代码不一定看得很明白且耗时
- 看书也得注意舒适度,如果看的章节比较晦涩难懂,放慢速度一点点看,太急导致一知半解反而效果不好,看懂了才有舒适度,否则还是很难受
Share
《算法导论》第13章 红黑树
之前看了一遍,全忘了,再复习一遍
前面章节显示一个高度为h的二叉搜索树支持任意基本动态集操作 - 比如搜索、前节点、后节点、最大值、最小值、插入和删除为O(h)时间复杂度。这样,集合操作很快如果搜索树的高度较小的话。如果高度很高,集合操作可能运行不比链表快。红黑树是许多搜索树解决方案的一种,它是平衡的为了确保基本动态集操作在最坏的情况下有O(lgn)的时间复杂度
红黑树属性
一个红黑树是一个二叉搜索树,每个节点额外带一个比特的存储:它的颜色,红色或黑色。通过限制从根到叶子的任意简单路径上的节点颜色,红黑树确保这样的路径不会比别的路径的长度超过两倍,这样该树是大约平衡的
树上每个节点现在包含属性颜色、键、左、右和父,如果一个节点的一个孩子或父不存在,对应的节点指针属性包含值NIL。我们将视这些NIL为指针到二叉搜索树叶子(额外节点)及正常,携带键的节点为树的内部节点
一个红黑树是一个二叉树满足如下红黑树属性:
- 每个节点要么红色要么黑色
- 根节点是黑色
- 每个叶子(NIL)是黑色
- 如果一个节点是红色,则它的两个孩子节点是黑色
- 对每个节点,从这个节点到其叶子节点所含的所有简单路径有相同数目的黑色节点
为了方便处理红黑树代码的边界条件,我们使用一个单个守卫符来代表NIL。对红黑树T,守卫符T.nil是一个和树中普通节点有相同属性的对象。它的颜色属性是黑色,它的其他属性 - 父、左、右和键可为任意值。所有指向NIL的指针被替换为指向守卫符T.nil
我们使用守卫符使得我们可处理节点x的一个NIL孩子节点作为父节点为x的普通节点。虽然我们在树中对每个NIL可以添加不同的守卫节点,这样每个NIL节点的父是良好定义的,但这样处理会浪费空间。我们使用一个守卫符T.nil代表所有的NILs - 所有叶子和根的父。守卫符父、左、右和键值可忽略,虽然我们在方便的时候可设置它们
我们一般限制我们的兴趣点在红黑树的内部节点,因为它们持有键值。在本章的剩下部分,当我们画红黑树时我们忽略叶子
我们称任意简单路径上黑色节点的数目,不包括节点x本身,从节点x到其叶子结点中的黑节点,记为bh(x)。我们定义红黑树的黑色高度为它根节点的黑色高度
引理 有n个内部节点的红黑树有高度最多2lg(n + 1)
证明:我们已显示在任意节点x为根的子树包含至少 $ 2^{hb(x)} - 1 $个内部节点开始。我们通过在x的高度上用归纳法证明。如果x的高度是0,则x必须为叶子(T.nil),且以x为根的子树包含至少 $ 2^{bh(x)} - 1 = 2^{0} - 1 = 0 $个内部节点。考虑一个节点有正数的高度且是有两个孩子节点的内部节点。每个孩子有一个黑色高度要么bh(x)或bh(x) - 1,取决于是否它的颜色是红或黑。因为x的孩子的高度小于x本身的高度,我们可应用归纳假设使每个孩子有至少 $ 2^{bh(x) - 1} - 1 $个内部节点。这样,x为根的子树包含至少 $ (2^{bh(x) - 1} - 1) + (2^{bh(x) - 1} - 1) + 1 = 2^{bh(x)} - 1 $ 个内部节点
为完成引理的证明,设h为树的高度。则从根到叶子的任意路径上至少一半的节点,不包含根,必须为黑色。结论,根的黑色高度必须至少h / 2,这样
$ \begin{equation} n \ge 2^{\frac{h}{2}} - 1 \end{equation} $
规整一下该该公式,可得 $ \lg (n + 1) \ge \frac{h}{2} 或 h \le 2 \lg (n+1) $
旋转
搜索树操作TREE-INSERT和TREE-DELETE,时间复杂度为O(lgn)。因为它们会修改树,结果会违反红黑属性。为恢复这些属性,我们必须改变树中某些节点的颜色且改变指针结构
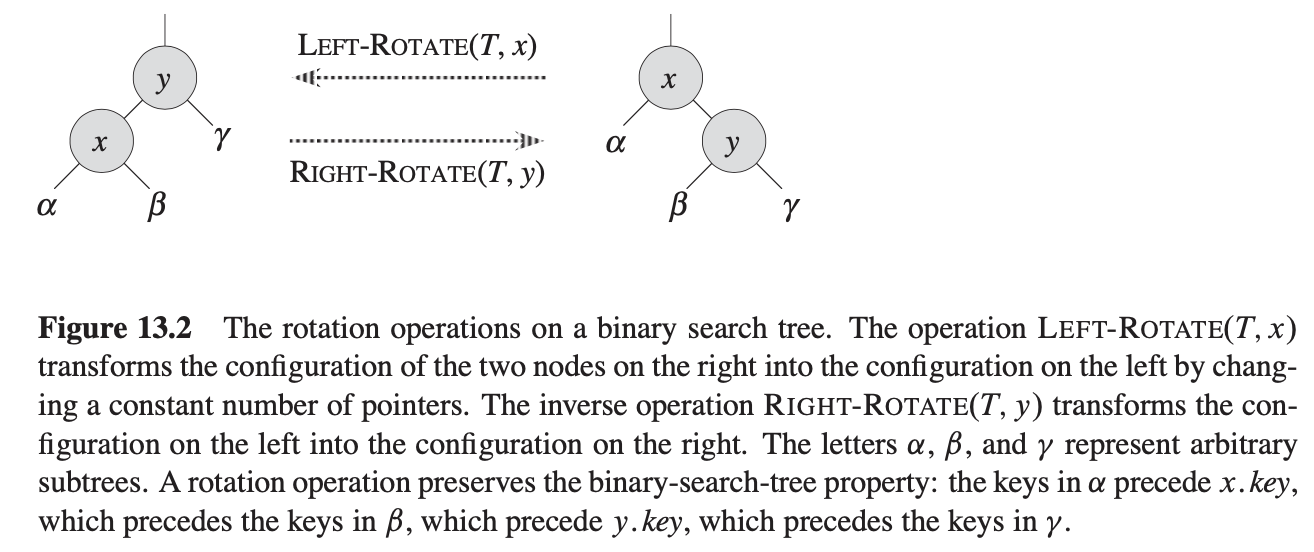
我们通过旋转来改变指针结构,其是一个搜索树中本地操作保留二叉搜索树属性。有两种类型的旋转:左旋和右旋。当我们在节点x上左旋时,我们假设它的右子节点不是T.nil;x可能为树中任意节点其右子节点不是T.nil。左旋使y作为子树的新根,x作为y的左子节点且y的左子节点作为x的右子节点
LEFT-ROTATE的伪代码假设 $ x.right \ne T.nil $且root的父为T.nil
$ \begin{equation} 1 \qquad y = x.right \qquad \qquad \text{set y} \\ 2 \qquad x.right = y.left \qquad \qquad \text{// turn y’s left subtree into x’s right subtree} \\ 3 \qquad \text{if } y.left \ne T.nil \\ 4 \qquad \qquad y.left.p = x \\ 5 \qquad y.p = x.p \qquad \qquad \text{// link x’s parent to y} \\ 6 \qquad \text{if } x.p == T.nil \\ 7 \qquad \qquad T.root = y \\ 8 \qquad \text{elseif } x == x.p.left \\ 9 \qquad \qquad x.p.left = y \\ 10 \qquad \text{else } x.p.right = y \\ 11 \qquad y.left = x \qquad \qquad \text{// put x on y’s left} \\ 12 \qquad x.p = y \end{equation} $
RIGHT-ROTATE代码跟LEFT-ROTATE代码是对称的,时间复杂度为O(1)
插入
我们能插入一个节点到n个节点的红黑树,时间复杂度为O(lgn)。为此,我们使用一个TREE-INSERT的直接修改版本插入节点z到树T,然后标记z为红色。为保持红黑树属性,我们然后调用一个辅助过程RB-INSERT-FIXUP来调整节点颜色并执行旋转。
$ \begin{equation} RB-INSERT(T, z) \\ 1 \qquad y = T.nil \\ 2 \qquad x = T.root \\ 3 \qquad \text{while }x \ne T.nil \\ 4 \qquad \qquad y = x \\ 5 \qquad \qquad \text{if } z.key < x.key \\ 6 \qquad \qquad \qquad x = x.left \\ 7 \qquad \qquad \text{else } x = x.right \\ 8 \qquad z.p = y \\ 9 \qquad \text{if } y == T.nil \\ 10 \qquad \qquad T.root = z \\ 11 \qquad \text{elseif } z.key < y.key \\ 12 \qquad \qquad y.left = z \\ 13 \qquad \text{else } y.right = z \\ 14 \qquad z.left = T.nil \\ 15 \qquad z.right = T.nil \\ 16 \qquad z.color = RED \\ 17 \qquad RB-INSERT-FIXUP(T, z) \end{equation} $
TREE-INSERT和RB-INSERT过程有四点不同。首先,TREE-INSERT中的所有NIL实例被T.nil替代。其次,我们在RB-INSERT的第14-15行设置z.left和z.right为T.nil,为了维护适合的树结构。第三,我们在第16行设置z节点颜色。第四,因为把z节点设置为红色可能违反了红黑树属性,我们在17行调用RB-INSERT-FIXUP(T, z)来恢复红黑树属性
$ \begin{equation} RB-INSERT-FIXUP(T, z) \\ 1 \qquad \text{while } z.p.color == RED \\ 2 \qquad \qquad \text{if } z.p == z.p.p.left \\ 3 \qquad \qquad \qquad y = z.p.p.right \\ 4 \qquad \qquad \qquad \text{if } y.color == RED \\ 5 \qquad \qquad \qquad \qquad z.p.color = BLACK \qquad \qquad \qquad \text{// case 1} \\ 6 \qquad \qquad \qquad \qquad y.color = BLACK \qquad \qquad \qquad \text{// case 1} \\ 7 \qquad \qquad \qquad \qquad z.p.p.color = RED \qquad \qquad \qquad \text{// case 1} \\ 8 \qquad \qquad \qquad \qquad z = z.p.p \qquad \qquad \qquad \text{// case 1} \\ 9 \qquad \qquad \qquad \text{else if } z == z.p.right \\ 10 \qquad \qquad \qquad \qquad z = z.p \qquad \qquad \qquad \text{// case 2} \\ 11 \qquad \qquad \qquad \qquad LEFT-ROTATE(T, z) \qquad \qquad \qquad \text{// case 2} \\ 12 \qquad \qquad \qquad \qquad z.p.color = BLACK \qquad \qquad \qquad \text{// case 3} \\ 13 \qquad \qquad \qquad \qquad z.p.p.color = RED \qquad \qquad \qquad \text{// case 3} \\ 14 \qquad \qquad \qquad \qquad RIGHT-ROTATE(T, z.p.p) \qquad \qquad \qquad \text{// case 3} \\ 15 \qquad \qquad \text{else (same as then clause with “right” and “left” exchanged)} \\ 16 \qquad T.root.color = BLACK \end{equation} $
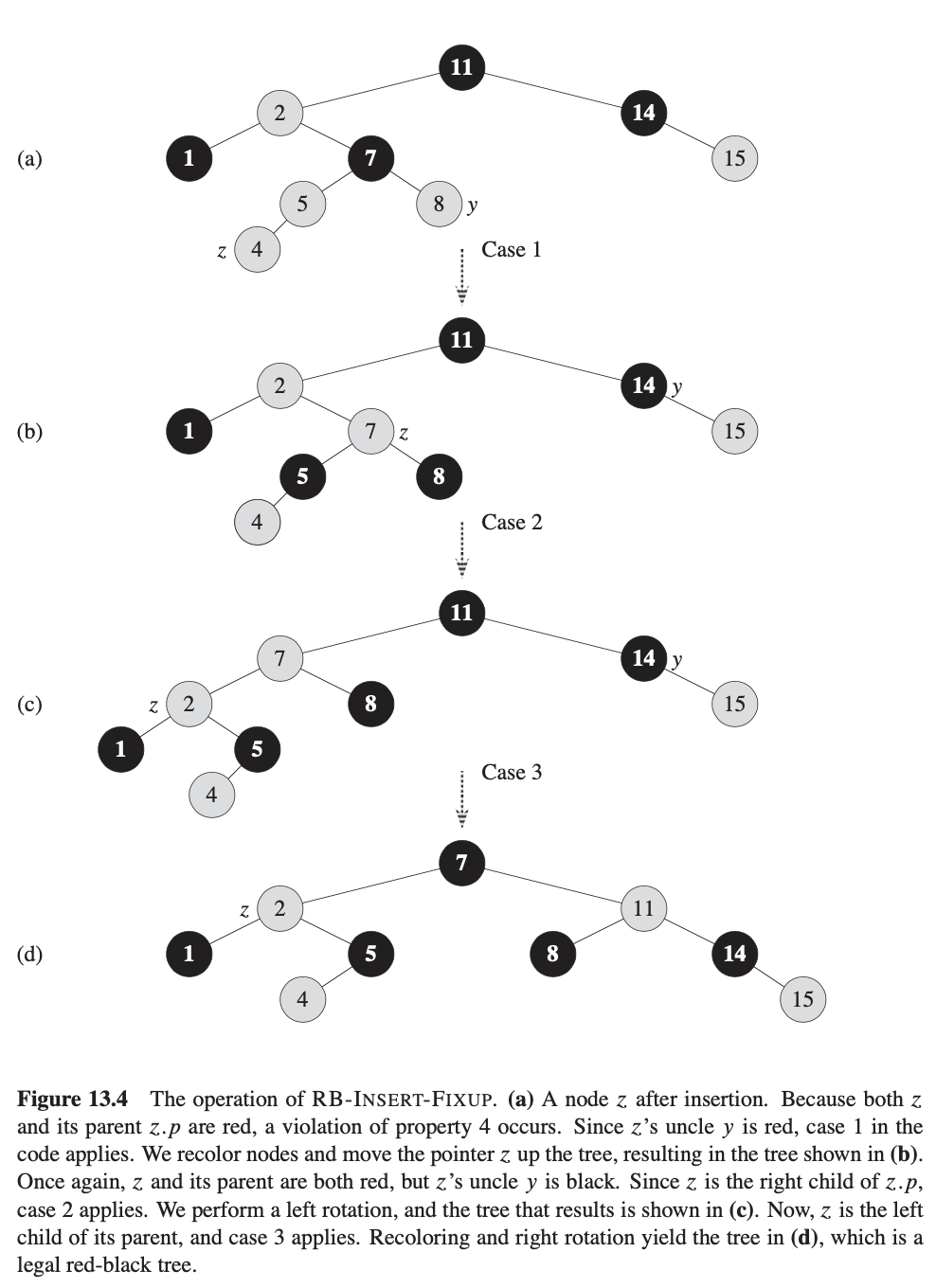
为理解RB-INSERT-FIXUP如何工作,我们应该把该代码分成3个主要步骤。首先,我们应该确定什么违反了红黑树属性当节点z被插入并设置为红色时被引入了进来。其次,我们应该检查1-15行while循环的整体目标。最后,我们应该探索while循环里3个分支的每一个并查看它们如何实现目标。上图显示了RB-INSERT-FIXUP在一个红黑树例子中的操作
红黑树的什么属性会在调用RB-INSERT-FIXUP时违背?属性1一直保持,属性3也是,因为新插入的红色节点的两个孩子为T.ni。属性5为从一个给定节点的每个简单路径有相同数目的黑节点,也满足,因为节点z替代了守卫符,且节点z是红色的。这样,唯一可能违反的属性是属性2,其要求根为黑色,且属性4,一个红色节点不能有一个红色的孩子。由于z是红色,这两个属性都可能违反。如果z是根,属性2被违反,如果z的父是红色,属性4被违反。上图显示在节点z被插入后属性4被违反
1-15行的while循环在每次循环迭代开始时维持如下三部分不变量:
a. 节点z是红色的
b. 如果z.p是根,则z.p是黑色的
c. 如果树违反红黑树的任意属性,则它违反最多其中一个,且要么属性2要么属性4。如果树违反属性2,它是因为z是根且是红色,如果违反属性4,它是因为z和z.p都是红色
c部分处理红黑树的违背情况。因为我们将聚焦在节点z和其附近节点,从a部分我们知道z是红色的,我们将使用b部分显示当我们引用它在第2、3、7、8、13和14行时节点z.p.p存在
回忆我们需要显示一个循环不变量是真的在循环第一次迭代之前,每次迭代维持循环不变量,且循环不变量在循环结束给了我们有用的属性
我们以初始化和终止参数开始。然后,当我们检查循环主体工作的细节,我们将讨论循环每次迭代时维持不变量。通过这个方法,我们也将显示循环的每次迭代有两个可能的输出:要么指针z在树上往上移,要么我们执行某些旋转并然后循环终止
初始化:在循环开始之前,我们的红黑树是正常的,然后我们添加一个红色节点z。我们显示在RB-INSERT-FIXUP被调用时不变量的每个部分都保持:
a. 当RB-INSERT-FIXUP被调用时,被添加的z节点是红色的
b. 如果z.p是根,则z.p变成黑且不改变之前的RB-INSERT-FIXUP调用
c. 我们已经看到当RB-INSERT-FIXUP被调用时属性1、3和5是保持的
如果树违反了属性2,则红色根必须为新添加的z节点,它是树中唯一的内部节点。因为z的父和孩子节点都是守卫符,颜色是黑,则树不违背属性4,这样,整个树的红黑属性只违背了属性2
如果树违反了属性4,则因为z的孩子节点为黑色守卫符且树在z添加之前不违反任何属性,则z和z.p都是红色
终止:当循环终止时,z.p是黑色。(如果z是根,则z.p是守卫符,也是黑色),这样在循环终止时树不违背属性4。通过循环不变量,唯一会违反的是属性2。16行恢复了该属性,这样当RB-INSERT-FIXUP结束时,所有的红黑树属性都保持了
维持:我们事实上在循环中需要考虑6种情况,但其中3种和另3种对称,依赖于是否第2行确定z的父z.p为z的祖父z.p.p的左孩子或右孩子。我们已给出z.p为左孩子时的代码。z.p.p节点存在,因为循环不变量的(b)部分。如果z.p是根,则z.p是黑色的。因为我们进入一个循环迭代只在z.p是红色的时候,我们知道z.p不可能为根。因此,z.p.p存在
我们通过z的父的兄弟节点的颜色区分case 1还是case 2和3。第3行使y指向z的叔叔z.p.p.right,第4行测试y的颜色。如果y为红色,则我们执行case 1。否则,执行case 2和3。在所有这3种情况中,z的祖父z.p.p是黑色的,因为它的父z.p是红色的,且属性4只在z和z.p之间被违背
第一种情况:z的叔叔y是红色
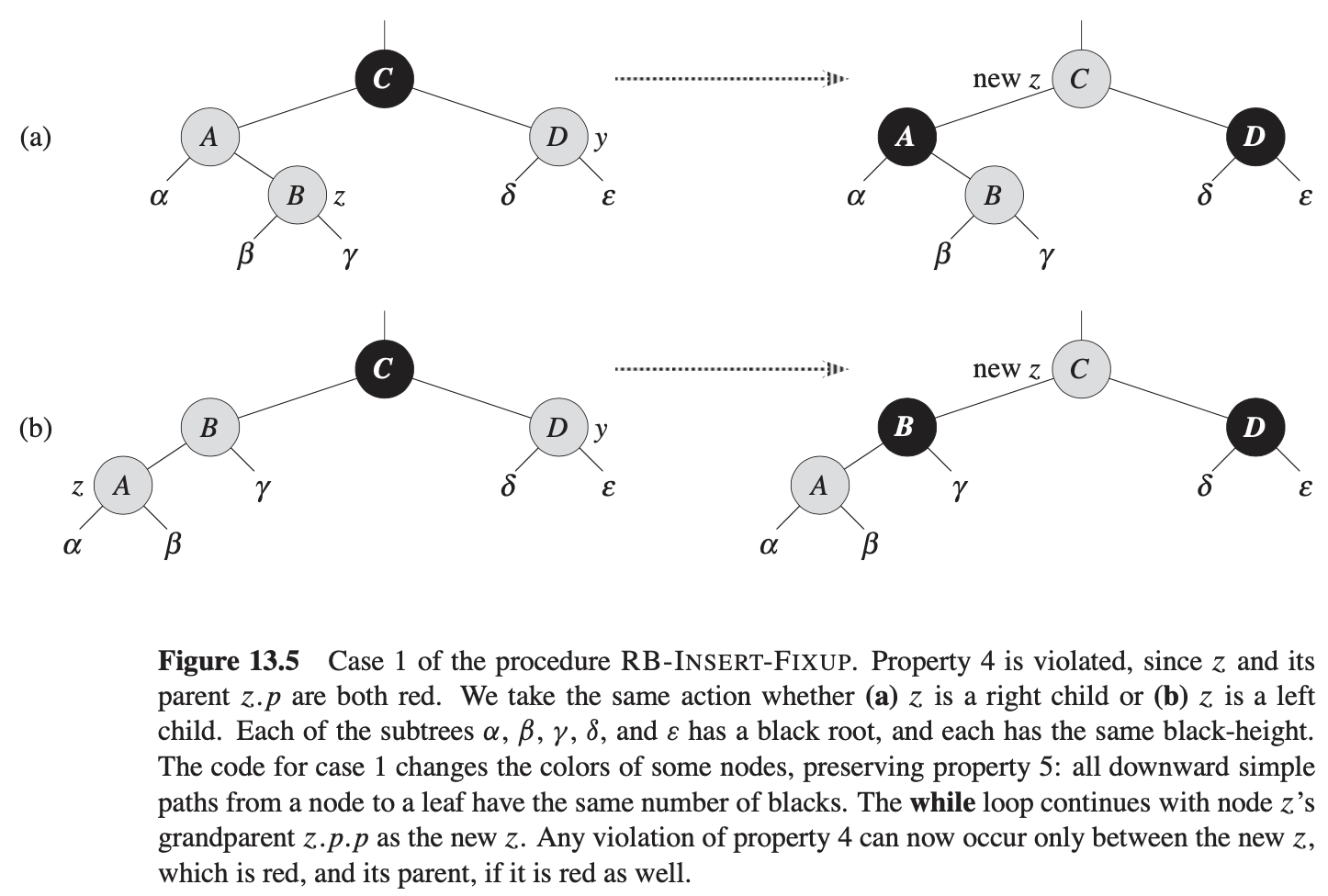
上图显示case 1(5-8行)的情形,当z.p和y都是红色时发生。因为z.p.p是黑色的,我们可设置z.p和y为黑色,因此修复了z和z.p都是红色的问题,且我们可设置z.p.p为红色,因此维护了属性5。我们然后把z.p.p作为z节点重复循环。z指针在树中向上移动两层
现在,我们显示了case 1在开始和下一次迭代前维持了循环不变量。我们使用z记为当前迭代的z节点,且 $ z’ = z.p.p $记为下一次迭代时将被第1行测试的z节点
a. 因为本次迭代z.p.p的颜色为红色,$ z’ $节点在下一次迭代开始时为红色
b. 节点 $ z’.p $在本次迭代时是z.p.p.p节点,且该节点颜色不变。如果这个节点是根,它在这次迭代前为黑色,且它在下一次迭代前仍然是黑色
c. 我们已经讨论了case 1维持了属性5,且它不引入属性1和3的违背问题
如果节点 $ z’ $在下一次迭代前是根,则case 1在本次迭代时纠正了属性4的违背问题,因为 $ z’ $是红色且它是根,属性2是唯一违背的属性
如果节点 $ z’ $在下一次迭代前不是根,则case 1纠正了本次迭代前出现的属性4违背问题,如果 $ z’.p $为黑色,则属性4不会违背,如果 $ z’.p $是红色,则 $ z’ $的红色使 $ z’和z’.p $之间出现属性4的违背问题
Case 2: z的叔叔y是黑色且z是一个右孩子
Case 3: z的叔叔是黑色且z是一个左孩子
在case 2和3中,z的叔叔颜色是黑色。我们区分这两个case根据z是z.p的右孩子还是左孩子。第10-11行为case 2,我们使用一个左旋来转换该形式为case 3(12-14行)。因为z和z.p都是红色,旋转不影响节点的黑色高度也不违背属性5。另外,z.p.p存在,因为我们已经讨论在第2、3行执行时该节点存在,且在第10行z往上移动一层后,在第11行会往下走一层。这样z.p.p没有改变。在case 3中,我们执行一些颜色改变且做一个右旋,使得属性5保持,而且我们不再有两个红色在一行。while循环不会再迭代,因为z.p现在是黑色
我们现在展示了case 2和3维持了循环不变量
a. case 2使z指向z.p,颜色是红色。之后在case 2和3中z和其颜色不会再改变
b. case 3使z.p为黑色,这样如果z.p是下一次迭代前的根,它是黑色
c. 属性1、3和5在case 2和3中得到保持
因为z节点在case 2和3中不是根,我们知道属性2不会被违背,case 2和3不会违背属性2,因为唯一红色的节点在case 3中被旋转变成黑色节点的孩子
case 2和3纠正了属性4的违背问题,且它们不引入其他的违背问题
因此循环的每次迭代都维持了不变量,我们以展示了RB-INSERT-FIXUP正确恢复了红黑树属性
分析
RB-INSERT的时间复杂度是多少?因为n个节点的红黑树的高度为O(lgn),RB-INSERT的第1-16行为O(lgn),在RB-INSERT-FIXUP中,while循环只在case 1时发生,然后z指针向上移动两层。while循环的总时间因此为O(lgn),这样,RB-INSERT时间复杂度为O(lgn)。它不会执行超过两次的旋转,因为while循环在case 2和3时会终止
删除
和其他基本操作一样在n个节点的红黑树上,删除一个节点的时间复杂度是O(lgn)。删除节点比插入节点要复杂一点
红黑树的删除过程基于前一章的TREE-DELETE过程。首先,我们需要自定义TANSPLANT子过程,红黑树中的TREE-DELETE会调用它:
$ \begin{equation} RB-TRANSPLANT(T, u, v) \\ 1 \qquad \text{if } u.p == T.nil \\ 2 \qquad \qquad T.root = v \\ 3 \qquad \text{elseif } u == u.p.left \\ 4 \qquad \qquad u.p.left = v \\ 5 \qquad \text{else } u.p.right = v \\ 6 \qquad v.p = u.p \end{equation} $
RB-TRANSPLANT有两个地方跟TRANSPLANT不同,首先,第1行指向守卫符T.nil而不是NIL。其次,在第6行无条件给v.p赋值:我们可赋值给v.p即使v指向守卫符。事实上,我们将利用这个特点赋值v.p当v = T.nil
RB-DELETE过程很像TREE-DELETE,但有额外的伪代码行。一些代码行保持跟踪y节点可能违反红黑树属性。当我们想要删除节点z且没有两个孩子,则z从树中删除,且我们想要y为z。当z有两个孩子,则y应该为z的继任者,且y移动到树中z的位置。我们也记录y的颜色在它删除或移动之前,且我们保持跟踪x节点移动到y的原始位置,因为x节点可能也违反了红黑树属性。在删除z节点后,RB-DELETE调用一个辅助过程RB-DELETE-FIXUP,它改变颜色且执行旋转来恢复红黑树属性
$ \begin{equation} RB-DELETE(T, z) \\ 1 \qquad y = z \\ 2 \qquad y-originnal-color = y.color \\ 3 \qquad \text{if } z.left == T.nil \\ 4 \qquad \qquad x = z.right \\ 5 \qquad \qquad RB-TRANSPLANT(T, z, z.right) \\ 6 \qquad \text{elseif } z.right == T.nil \\ 7 \qquad \qquad x = z.left \\ 8 \qquad \qquad RB-TRANSPLANT(T, z, z.left) \\ 9 \qquad \text{else } y = TREE-MINIMUM(z.right) \\ 10 \qquad \qquad y-original-color = y.color \\ 11 \qquad \qquad x = y.right \\ 12 \qquad \qquad \text{if } y.p == z \\ 13 \qquad \qquad \qquad x.p = y \\ 14 \qquad \qquad \text{else } RB-TRANSPLANT(T, y, y.right) \\ 15 \qquad \qquad \qquad y.right = z.right \\ 16 \qquad \qquad \qquad y.right.p = y \\ 17 \qquad \qquad RB-TRANSPLANT(T, z, y) \\ 18 \qquad \qquad y.left = z.left \\ 19 \qquad \qquad y.left.p = y \\ 20 \qquad \qquad y.color = z.color \\ 21 \qquad \text{if } y-original-color == BLACK \\ 22 \qquad \qquad RB-DELETE-FIXUP(T, x) \end{equation} $
虽然RB-DELETE包含TREE-DELETE大约两倍的代码,这两个过程还是相同的基本结构。你可找到TREE-DELETE的每一行对应到RB-DELETE(变化是用T.nnil替代NIL和调用RB-TRANSPLANT替代TRANSPLANT),在相同的条件下执行
以下是两个过程间其他的不同:
- 我们维持节点y要么从树中删除要么在树中移动。第1行设置y指向z节点,当z节点没有两个孩子时且因此被删除。当z有两个孩子,第9行设置y指向z的继任者,且y将移动到z的位置
- 因为y的颜色可能改变,变量y-orignal-color存储y原来的颜色。第2行和第10行在赋值到y后设置该变量,当z有两个孩子时,则 $ y \neq z $,且y节点移动到z节点原来的位置;第20行设置y跟z一样的颜色。我们需要保存y的原来的颜色为了在RB-DELETE的最后测试它;如果它是黑色,则删除或移动y将违背红黑树属性
- 我们保持跟踪x节点移动到y原来的位置。在第4、7和11行设置x指向要么y的唯一孩子要么y没有孩子则为守卫符T.nil
-
因为x节点移动到y原始的位置,属性x.p总是设置为y原始位置时的父,即使x是守卫符T.nil。除非z是y原来的父(当z有两个孩子且它的继任者y是它的右孩子),在RB-TRANSPLANT的第6行赋值给x.p(观察到当RB-TRANSPLANT在第5、8和14行被调用时,第二个参数是x)
当y原始的父为z,然而,我们不想x.p指向y原始的父,因为我们已移除该节点。因为y节点将移动并占据z的位置,在第13行设置x.p为y使x.p指向y的父的原始位置,即使x为T.nil
- 最后,如果y节点为黑色,我们将引入一个或多个红黑树属性违背问题,且这样我们在第22行调用RB-DELETE-FIXUP来恢复红黑树属性。如果y为红色,当y被删除或移动时红黑树属性仍然保持,原因如下:
-
树中黑色高度没有改变
-
没有红色节点邻接。因为y占据z的位置,及为z的颜色,我们不能有两个邻接红色节点在y的新位置。另外,如果y不是z的右孩子,则y的原始右孩子x替代y。如果y是红色,则x必须为黑色,且这样x替代y不会引起两个红色节点邻接
-
因为y如果是红色则不会为根,根仍然是黑色
-
如果y节点是黑色,可能引起三个问题,调用RB-DELETE-FIXUP可解决。首先,如果y为根且y的一个红色孩子变成新的根,违反了属性2。其次,如果x和x.p为红色,则违反了属性4。第三,移动y导致之前包含y的任意简单路径少一个黑色节点。这样,属性5被y的任意祖先违反。我们可纠正属性5的问题,x节点现在占据y的原始位置,有一个额外的黑。即,如果我们添加1到包含x的任意简单路径的黑色节点数,则属性5保持。当我们删除或移动黑色y节点,我们把黑色给x节点。现在的问题是x节点要么是红色要么黑色,违反了属性1。x节点要么“双黑”要么“红和黑”,且它对应贡献2或1到包含x的简单路径的黑色节点数。x的颜色属性将要么红色(如果x是红和黑)或黑色(如果x是双黑)。即节点上额外的黑映射到x指向的点而不是颜色属性
我们现在看RB-DELETE-FIXUP过程并检查它如何恢复红黑属性
$ \begin{equation} RB-DELETE-FIXUP(T, x) \\ 1 \qquad \text{while } x \neq T.root \text{ and } x.color == BLACK \\ 2 \qquad \qquad \text{if } x == x.p.left \\ 3 \qquad \qquad \qquad w = x.p.right \\ 4 \qquad \qquad \qquad \text{if } w.color == RED \\ 5 \qquad \qquad \qquad \qquad w.color = BLACK \qquad \qquad \qquad \text{// case 1} \\ 6 \qquad \qquad \qquad \qquad x.p.color = RED \qquad \qquad \qquad \text{// case 1} \\ 7 \qquad \qquad \qquad \qquad LEFT-ROTATE(T, x.p) \qquad \qquad \qquad \text{// case 1} \\ 9 \qquad \qquad \qquad \text{if } w.left.color == BLACK \text{ and } w.right.color == BLACK \\ 10 \qquad \qquad \qquad \qquad w.color = RED \qquad \qquad \qquad \text{// case 2} \\ 11 \qquad \qquad \qquad \qquad x = x.p \qquad \qquad \qquad \text{// case 2} \\ 12 \qquad \qquad \qquad \text{else if } w.right.color == BLACK \\ 13 \qquad \qquad \qquad \qquad \qquad w.left.color = BLACK \qquad \qquad \qquad \text{// case 3} \\ 14 \qquad \qquad \qquad \qquad \qquad w.color = RED \qquad \qquad \qquad \text{// case 3} \\ 15 \qquad \qquad \qquad \qquad \qquad RIGHT-ROTATE(T, w) \qquad \qquad \qquad \text{// case 3} \\ 16 \qquad \qquad \qquad \qquad \qquad w = x.p.right \qquad \qquad \qquad \text{// case 3} \\ 17 \qquad \qquad \qquad \qquad w.color = x.p.color \qquad \qquad \qquad \text{// case 4} \\ 18 \qquad \qquad \qquad \qquad x.p.color = BLACK \qquad \qquad \qquad \text{// case 4} \\ 19 \qquad \qquad \qquad \qquad w.right.color = BLACK \qquad \qquad \qquad \text{// case 4} \\ 20 \qquad \qquad \qquad \qquad LEFT-ROTATE(T, x.p) \qquad \qquad \qquad \text{// case 4} \\ 21 \qquad \qquad \qquad \qquad x = T.root \qquad \qquad \qquad \text{// case 4} \\ 22 \qquad \qquad \text{else (same as then clause with “right” and “left” exchanged)} \\ 23 \qquad x.color = BLACK \end{equation} $
RB-DELETE-FIXUP过程恢复属性1、2和4,练习13.4-1和13.4-2要求你显示本过程恢复属性2和4,所以本节剩余部分我们讲集中于属性1。第1-22行循环的目的是移动额外的黑往上直到
- x指向一个红和黑节点,这样我们在第23行设置x颜色为黑色
- x指向根,我们简单移除额外的黑;或
- 已执行适当的旋转和颜色重设置,我们退出循环
在while循环中,x总是指向一个非根的双黑节点。我们在第2行确定是否x是一个左孩子或一个右孩子。(我们给出x是左孩子的情形的代码;右孩子的代码是对称的)我们维护一个指针w为x的兄弟。因为x节点是双黑,w节点不能为T.nil,因为否则从x.p到(单黑)叶子w的简单路径黑色数目讲比x.p到x的简单路径数目少
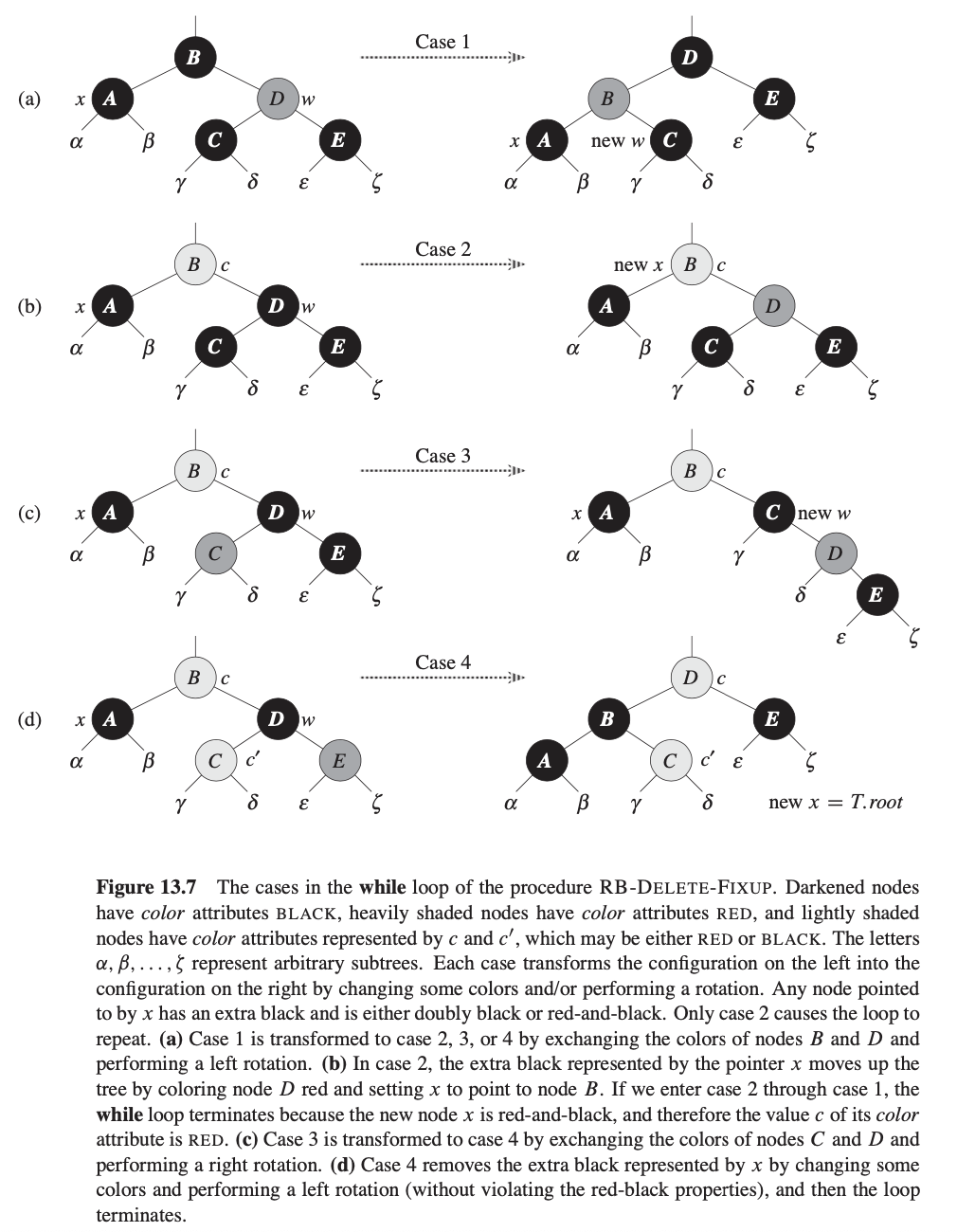
第4个case在上图中,在检查每个case细节之前,让我们更一般化地看看我们可如何检查每个case中的转换保持属性5。关键点是在每个case中,转换应用保留黑色节点数(包括x的额外黑色)从(包括)每个子树 $ \alpha, \beta, \ldots, \zeta $的根。这样,如果属性5在转换之前保持,它会继续保持。例如,在上图(a)中,即case 1,从根到子树 $ \alpha, \beta $的黑色节点数在转换前和转换后都是3。(记住x节点会有一个额外的黑)相似的,从根到任意 $ \gamma, \delta, \sigma, \zeta $的黑色节点数在转换前和转换后都是2。在上图(b)中,计数必须包含根的子树的c值的颜色属性,其可能为红或黑。如果我们定义count(RED) = 0及count(BLACK) = 1,则从根到 $ \alpha $的黑色节点数在转换前和转换后都是2 + count(c),在这个case中,转换之后,x新节点有颜色属性c,但这个节点要么黑和红(如果c = RED)或双黑(如果c = BLACK)。你可相似地检查其他cases
Case 1: x的兄弟节点w是红色
case 1(RB-DELETE-FIXUP的第5-8行和上图(a))发送在当x的兄弟节点w为红色时。因为w必须有黑色孩子,我们可交换w和x.p的颜色且然后在x.p上执行不会违背任何红黑属性的左旋。新的x兄弟节点,是旋转前的w的一个孩子节点,现在是黑色,且这样我们转换case 1为case 2、3或4
case 2、3、4发生在当w节点为黑色,它们的不同在w的孩子的颜色
Case 2: x的兄弟节点w是黑色,w节点的两个孩子为黑色
在case 2(RB-DELETE-FIXUP的第10-11行和上图(b))中,w的两个孩子为黑色。因为w也是黑色的,我们从x和w中移除一个黑,使x只有一个黑,w为红色。为补偿从x和w中移除的黑色,我们将添加一个额外的黑色给x.p,x.p原来是红色或黑色。我们这样重复while循环使x.p作为新的x节点。观察到如果我们从case 1进入case 2,新的x节点是红和黑色,因为原本的x.p是红色。因此,新x节点的c值颜色属性是红色,且当它测试循环条件时循环结束。我们然后把新x节点在第23行设置为黑色
Case 3: x的兄弟节点w是黑色,w的左孩子是红色,且w的右孩子是黑色
在case 3(第13-16行且上图(c))中,发生时w是黑色,它的左孩子是红色,且它的右孩子是黑色。我们可交换w和w.left的颜色然后在w上执行一个不违背任何红黑属性的右旋。新的x兄弟节点w是一个黑色节点带一个红色右孩子,这样我们转换case 3为case 4
Case 4: x的兄弟w节点是黑色,w的右孩子是红色
case 4(第17-21行和上图(d))发生在当x的兄弟节点w是黑色且w的右孩子是红色。通过改变一些颜色和在x.p上执行一个左旋,我们可移除x节点上额外的黑色,且不违背任何红黑属性。设置x为根导致while循环终止当它测试该循环条件时
分析
RB-DELETE的时间复杂度是多少?因为一个n个节点的红黑树高度为O(lgn),过程的总开销除了RB-DELETE-FIXUP为O(lgn)。而RB-DELETE-FIXUP,case 1、3和4在执行一些颜色改变和最多3个旋转后终止,case 2是唯一的使while循环继续,然后x指针往上移动最多O(lgn)次且执行最多3次旋转,RB-DELETE的总时间也是O(lgn)