Table of Contents
Algorithm
Leetcode 347: Top K Frequent Elements
https://dreamume.medium.com/leetcode-347-top-k-frequent-elements-d38cd70541fe
Review
Epidemic Algorithms for Replicated Database Maintenance
简介
考虑数据库在大型、各种各样、不可靠且缓慢改变的成百上千个网站的网络环境下的对许多网站复制,我们检查一些方法在站点间达成并维持一致。每个数据库更新被注入在单个站点且必须广播到所有其他站点或被后续的更新替代。站点可变成全一致仅当所有的更新活动已停止且系统暂时变得安静。另一方面,假设一个合理的更新速度,大多数信息在任意给定站点是当前的。这个一致性的松散形式在实际中很有用。我们的目标是设计高效稳定的算法且能很好的使用站点增长的扩展
在检查算法解决这个问题的可考虑重要因素包括
- 更新需要的时间广播到所有站点,且
- 广播单个更新产生的网络流量。理想网络流量是跟更新乘以服务器数量成比例的,但一些算法产生更多的流量
本文我们呈现分析,使用扩散更新的一些策略的模拟结果和实践经验。方法检查包括;
- 直接邮件:每个新的更新直接从该站点邮件到所有其他站点。这是有效的但不是完全可靠因为个别站点不总是知道所有其他站点且邮件有时会丢失
- 反熵:每个站点随机规律地选择另一个站点且交换它解决的两者之间不同的数据库内容。反熵是非常可靠的但需要检测数据库内容且不能使用太频繁。分析和模拟显示反熵,可靠、广播更新比直接邮件慢很多
- 谣言传播:站点初始化为“无知的”,当一个站点接收到一个新的更新它变成一个“热谣言“;当站点持有一个热谣言,它定期随机选择一个其他站点并确保该站点已看到该更新;当站点已经尝试共享一个热谣言给很多站点以看到该更新,站点停止对待谣言为热的且不再广播该更新。谣言循环可能比反熵更频繁因为它们在每个站点上要求更少的资源,但有几率导致更新不会达到所有站点
反熵和谣言传播都是传染进程的例子,传染理论的结果是可应用的。这些机制的理解极大地得利于现存的流行病数学理论,虽然我们的目的不同。更多地,我们有设计流行病机制的自由,我们采用流行病领域的术语并称有一个更新要共享的站点为共享该更新的感染。一个站点为易感染的如果它还未接收到更新;一个站点被删除如果它接收到更新但不再共享更新。反熵是一个简单流行病的例子:站点总是要么易感染要么已感染
选择合作者统一结果会有高网络流量,使我们考虑相关分布其选择趋向于附近的服务器。施乐公司因特网在实际拓扑上的分析和模拟揭露了反熵和谣言传播的分布收敛和统一分布一样快,当减少每个连接的平均和最大流量时。结果反熵算法安装在施乐公司因特网且得到显著的性能改进
我们将指出数据库的扩展复制是昂贵的。它将通过数据库分层分解或缓存尽可能避免。即使这样,我们论文的结果是有趣的因为它们显示了显著的重复可被达到,通过简单的算法,在分层的每层或缓存方案上
动机
这个工作起源于在施乐公司Clearinghouse服务器的学习。公司组成数百个以太网用网关连接且许多不同容量的电话线。几千个工作站,服务器和计算主机。一个从日本机器来的包到欧洲可能经过了最多14个网关和7个电话线
Clearinghouse服务维护3层、分层名称到机器地址、用户唯一标识等的传递。分层分区上两层的名字空间到一个域集合。每个域可能存储(重复)一部分,或全部的Clearinghouse服务器,有数百个
一些域事实上存储在CIN的所有Clearinghouse服务器上。在1986年初,许多网络观察性能问题可被跟踪到在它们的高层复制域创建尝试达成一致流量上。随着网络增长,更新域存储在甚至几个服务器上广播也非常慢
当我们开始处理该问题,Clearinghouse服务器被用来直接邮件和反熵。反熵运行在每个域,理论上,每天本地时间在午夜到早上6点一次(每个服务器)。事实上,服务器由于网络负载经常不能在允许时间内完成反熵工作
我们首次发现反熵跟着一个重邮步骤:正确的数据库值被邮给之前两个反熵参与者分歧的所有站点。更多地站点间不同意导致更多的流量。对一个存储在300个站点的域,每天晚上可能有90000个邮件信息被引入。这远超网站的容量,且结果导致所有网络服务下线:邮件、文件传输、名字查询等等
因为重邮步骤不能在我们观察的大网络上工作,它被禁止。更进一步分析显示这没有效率:某些网络中key链接仍然被反熵流量过载
相关工作
本文算法想要维护一个广复制目录,或名称查找,数据库。跟使用基于交易的机制不同这里尝试达成“一次拷贝序列化“,我们使用驱动复制节点达到最终同意的机制。这样的机制被Johnson et al首先提出,并用在Grapevine和Clearinghouse中。这些系统的经验使我们知道一些问题仍在;特别地,一些更新(低可能性)不能到达所有站点。Lampson提出一个分层数据结构避免高复制,但仍然需要一些每个部件的复制,6到12个服务器。主站点复制数据库的更新算法被提议通过请求应用于单个站点来同步更新;更新站点负责广播更新到所有节点。DARPA域系统,例如,使用这种排序的算法。主站点更新避免了本文描述的分布式更新的问题但导致了集中控制
有两个特征区别我们的算法和之前的机制。首先,之前的机制依赖各种从底层通讯协议的保证和维持一致的分布式控制结构。例如,在Clearinghouse中更新的初始分布依赖于底层保障邮件协议,其在实际中由于物理查询过载经常故障,即使邮件队列维护在磁盘存储。Sarin和Lynch展现了一个分布式算法用来丢弃过时的数据,其依赖于保障,合适地顺序,消息转发及每个服务器描述相同数据库的其他所有服务器的具体数据结构。Lampson et al.预想一个服务器环上的确定性移动,被一个服务器到下一个的指针持有。这些算法依赖各种分布式数据结构的排斥一致属性,例如,在Lampson算法中指针必须定义为一个环。本文算法仅依赖重复消息的最终转发,不需要服务器的数据结构描述信息
其次,本文描述的算法是随机的,即每个服务器的算法使用独立的随机选择。不同地是,之前的机制是确定性的。例如,在反熵和流言触发算法中,一个服务器做一个随机选择要么依然感染或被删除。随机选择的使用避免我们使用这样的声明:“信息将以时间成比例的收敛到网络直径。“我们最好声称在更进一步的更新缺失的情况下,信息不能收敛的概率随时间指数级增长。另一方面,我们相信随机协议的使用使我们的算法可用简单的数据结构直接实现
本文计划
第一节形式化复制数据库的记号和展现达成一致性的基本技术。第二节描述从数据库删除数据项的技术;删除比其他改变更复杂因为删除数据项必须呈现一个替代者直到删除的消息扩散到所有站点。第3节展现反熵和流言合作者的选择在非统一空间分布上的模拟和分析结果
基本技术
本节介绍复制数据库记号和呈现基本直接邮件,反熵和复杂传染协议及它们的分析
记号
考虑一个网络包含n个站点的集合S,每个存储一个数据库的拷贝。数据库拷贝站点 $ s \in S $是时间变动的不完整函数
$ \begin{equation} s.ValueOf: K \to (v: V \times t : T) \end{equation} $
K是键的集合(名称),V是值的集合,T是时间戳的集合。V包含不同的元素NIL但未指明。T是按<总序。我们解释s.ValueOf[k] = (NIL, t)为该项目确认为k已经被从数据库中删除。即,从数据库客户端来看,s.ValueOf[k] = (NIL, t)就是s.ValueOf[k]未定义
第1.2和1.3节所述的分布式技术是简单的,通过考虑一个数据库对单个名称存储值和时间戳。所以我们说
$ \begin{equation} s.ValueOf \in (v: V \times t: T) \end{equation} $
例如,s.ValueOf是有序对包含一个值和一个时间戳。如之前所述,第一个元素可能是NIL,表示该项目在第二个元素所示的时间被删除
更新分布式进程的目标是驱动系统使得
$ \begin{equation} \forall s,s’ \in S, s.ValueOf = s’.ValueOf \end{equation} $
在任意站点有一个操作客户端必须调用来更新数据库,s:
$ \begin{equation} Update[v: V] \equiv s.ValueOf \gets (v, Now[]) \end{equation} $
Now是一个函数返回全局唯一时间戳。Now[]返回的时间戳将是当前的格林尼治时间 - 如果不是,算法将不以实际效果工作。感兴趣的读者可参考Clearinghouse[Op]和Grapevine[Bi]论文进一步地描述时间戳在构建一个有用的数据库中的角色。对我们的目的来说,必要地知道该元组有一个更大的时间戳将总是被替换成一个更小的时间戳
直接邮件
直接邮件策略当一个更新发生时尝试通知所有其他站点。基本的算法执行在一个站点上:
$ \begin{equation} \text{FOR EACH } s’ \in S \text{ DO} \\ \qquad PostMail[to: s’, msg: (“Update”, s.ValueOf)] \\ \qquad ENDLOOP \end{equation} $
一旦接受到消息(“Update”, (v,t)),站点执行:
$ \begin{equation} \text{IF } s.ValueOf.t < t \text{ THEN} \\ \qquad s.ValueOf \gets (v, t) \end{equation} $
PostMail操作希望是附近的,但不完全可靠。它把消息放入队列使得发送者不被延迟。队列保持在邮件服务器的稳定存储这样它们不被服务器崩溃影响。尽管,PostMail可能失败:消息可能被丢弃当队列满了或它们的目标长时间不能访问。除了邮件系统的这种故障,直接邮件也可能失败当源站点更新时没有S的精确知识,站点集合。
在Grapevine系统[Bi]中,检测和校正直接邮件故障的职责策略被指定给管理网络的人员。只有在几十个服务器的网络中这种处理方式才能很好适配
每个更新直接邮件产生n个消息,每个消息游走于源和目的之间的网络连接。这样(连接 $ \cdot $ 消息)流量单位跟站点数量乘以站点间平均距离成比例
反熵
Grapevine设计者认识到直接邮件处理故障在大型网络中超出了人的能力范围。他们提出反熵作为一个机制运行在从这样的故障中自动恢复的背景环境中。反熵不作为Grapevine的一部分来实现,但设计能在不变动的情况下适配Clearinghouse。它最基本的形式反熵被表达为如下在每个站点s上定期执行的算法:
$ \begin{equation} \text{FOR SOME } s’ \in S \text{ DO} \\ \qquad ResolveDifference[s, s’] \\ \qquad ENDLOOP \end{equation} $
ResolveDifference[s, s’]需要两个服务器合作,依赖于它的设计,它的有效方法可被表达为如下三种方式之一,称为push,pull和push-pull:
$ \begin{equation} ResolveDifference: PROC[s, s’] = \{ – push \\ \qquad \text{IF } s.ValueOf.t > s’.ValueOf.t \text{ THEN} \\ \qquad \qquad s’.ValueOf \gets s.ValueOf \\ \qquad \} \end{equation} $
$ \begin{equation} ResolveDifference: PROC[s, s’] = \{ – pull \\ \qquad \text{IF } s.ValueOf.t > s’.ValueOf.t \text{ THEN} \\ \qquad \qquad s’.ValueOf \gets s.ValueOf \\ \qquad \} \end{equation} $
$ \begin{equation} ResolveDifference: PROC[s, s’] = \{ – push-pull \\ \qquad \text{SELECT TRUE FROM } \\ \qquad \qquad s.ValueOf.t > s’.ValueOf.t \Rightarrow s’.ValueOf \gets s.ValueOf; \\ \qquad \qquad s.ValueOf.t < s’.ValueOf.t \Rightarrow s.ValueOf \gets s’.ValueOf; \\ \qquad \qquad ENDCASE \Rightarrow NULL; \\ \qquad \} \end{equation} $
现在我们假设站点s’被随机从集合S中统一选中,且每个站点每个时期执行一次反熵算法
它是流行病的基本结果即简单的流行病,比如反熵,最终感染整个人群。理论也显示开始的单个感染站点在预期时间内达成人口大小比例的日志。比例常量是敏感的对使用的ResolveDifference过程。对push,对大的n [Pi] 公式是 $ \log_ {2}(n) + \ln(n) + O(1) $
容易知道即使邮件失败,即扩散一个更新超过单个站点,则反熵将最终把它分布到整个网络。然而,我们期望反熵分布更新只到几个站点,假设多数站点通过直接邮件接收它们。这样,考虑当只有几个站点仍然是怀疑状态时会发生什么是很重要的。这种情况下push和pull之间行为有大不同,push-pull行为像pull。一个简单的确定性模型预测被观察的行为。设 $ p_ {i} $为在 $ i^{th} $反熵循环后一个站点仍然被怀疑的概率。对pull,如果它在 $ i^{th} $循环后被怀疑则站点在 $ i + 1^{st} $循环依然被怀疑且它在 $ i + 1^{st} $循环中联系一个怀疑站点。这样,我们获得
$ \begin{equation} p_ {i+1} = (p_ {i})^{2} \end{equation} $
当 $ p_ {i} $很小时会快速收敛到0。对push,一个站点如果在 $ i^{th} $循环中被怀疑则仍然在 $ i + 1^{st} $循环中被怀疑且没有感染站点在 $ i + 1^{st} $循环中选择联系它。这样,push的模拟发生为
$ \begin{equation} p_ {i+1} = p_ {i}\left(1 - \frac{1}{n}\right)^{n(1-p_ {i})} \end{equation} $
其也收敛到0,但相对慢些,因为对非常小 $ p_ {i} $(且大n)它大约是
$ \begin{equation} p_ {i+1} = p_ {i}e^{-1} \end{equation} $
强烈建议在实际中,当反熵被用来作为一个某些其他分布式机制比如直接邮件的备份,要么pull或push-pull比push要好,后者在理想情况下行为性能差
反熵算法非常昂贵,因为它包含一个数据库的两个完全拷贝的比较,其中一个来自网络。通常数据库拷贝是几乎完全同意,这样多数工作被浪费。给定这个观察,一个可能的性能改进对每个站点是维护一个数据库内容的checksum,当数据库更新时重新计算checksum。站点执行反熵首先交换checksum,只在checksum不匹配时比较全部的数据库。这个方案节省了大量的网络流量。不幸地是,通常最近的更新只有部分站点知道。checksum在不同的站点很可能不匹配除非时间需要一个更新发送给所有站点是很小的对应新更新间期望的时间。随着网络的增长,需要分布一个更新到所有站点的时间也增长,这样checksum的使用变得用处有限
一个更复杂的处理是使用checksum定义一个时间窗 $ \tau $,其足够大使得更新期望在 $ \tau $时间内到达所有站点。和简单方案一样,每个站点维护它的数据库checksum。另外,站点维护一个最近更新列表,一个在它的数据库中所有条目其年龄(通过它们的时间戳和站点本地时钟的不同度量)小于 $ \tau $的列表。两个站点s和s’执行反熵通过先交换最近更新列表,使用列表来更新它们的数据库和checksums,且然后比较checksums。只有checksums不匹配这些站点比较它们整个数据库
在比较checksums之前交换最近更新列表确保如果一个站点最近已接收到一个改变或删除,对应的丢弃条目不被计算在其他站点的checksum中。这样,checksum比较很可能成功,使全数据库比较成为不必要。在这样的情况下,反熵比较产生的期望的流量仅是最近更新列表的期望大小,为时间 $ \tau $内网络中发生的更新的数量。注意 $ \tau $的选择超过一个更新期望的分布时间是严重的事,如果 $ \tau $选择不好,或如果网络的增长驱使期望更新分布时间超过 $ \tau $,checksum比较将总是失败且网络流量将升高到被反熵产生没有checksum更高的水平
以上方案的一个简单变种,其不需要 $ \tau $值的有效选择,如果每个站点可维护一个通过时间戳的它的数据库的反转索引。两个站点执行反熵通过交换反向时间戳顺序更新,渐增地计算它们的checksums,直到checksum的一致达成。当从网络流量观点看它是理想的,该方案(我们将因此指定为peel bakc)可能并不实际因为维护每个站点额外的反转索引是昂贵的操作
复杂的污染流行
如我们所看到的,直接邮件更新有几个问题:它可能失败因为消息丢失,或因为起源处有其他数据库站点的不完全信息,且它在起源站点引入一个O(n)的瓶颈。这些问题的一些被一个广播邮件机制弥补,但大多数该机制依赖一个分布信息。我们将要描述的流行机制能避免这些问题,但它们有一个不同的、直接故障的可能性必须小心地学习分析和模拟。幸运地是这个故障可能性可任意小。我们指定这些机制为复杂的流行用来区分反熵对应简单的流行;复杂流行仍然有一个简单的实现
回忆单个更新,一个数据库要么怀疑(它不知道该更新),感染(它知道该更新且与其他站点共享)或删除(它知道该更新但不扩散它)。这非常容易实现使得一个共享的步骤不需要完全的访问数据库。发送者管理一个感染更新的列表,且接收者尝试插入每个更新到它自己的数据库且添加所有新的更新到它的感染列表。唯一的难点是决定什么时候从感染列表中删除更新
在我们讨论设计好的传染之前,让我们看一个例子,通常称为流言扩散
流言扩散基于如下的场景:有n个人,初始化未激活(怀疑)。我们散布一个人的流言使其激活(感染),随机电话其他人且共享流言。每个人听到流言也变激活且分享流言。当一个激活的人用一个不必要的电话拨打(接收者已知道流言),则有概率1/k该激活的人失去共享流言的兴趣(该人变得被删除)。我们将知道系统如何快的收敛到未激活状态(该状态下没有人被感染)且当该状态达成时知道流言的人的百分比
以下描述,流言扩展可能被确定性的用一对积分等式建模。我们设s, i和r代表怀疑的人的比例,感染的比例和删除的比例,这样s + i + r = 1:
$ \begin{equation} \frac{ds}{dt} = -si \end{equation} $
$ \begin{equation} \frac{di}{dt} = +si -\frac{1}{k}(1 -s)i \end{equation} $
第一个等式建议怀疑者将根据乘积si被感染,第二个等式有一个额外的项表达由于不必要的电话呼叫导致的丢失。第三个等式对r是冗余的
处理以上等式一个标准的技术是使用比率。消除t且让我们解决i作为s的一个函数:
$ \begin{equation} \frac{di}{ds} = - \frac{k+1}{k} + \frac{1}{ks} \end{equation} $
$ \begin{equation} i(s) = - \frac{k+1}{k}s + \frac{1}{k} \log s + c\end{equation} $
c是一个积分常量被初始条件决定:$ i(1 - \epsilon) = \epsilon $
对大n,$ \epsilon $为0,给定:
$ \begin{equation} c = \frac{k+1}{k} \end{equation} $
且一个解决方案
$ \begin{equation} i(s) = \frac{k+1}{k}(1 - s) + \frac{1}{k} \log s \end{equation} $
函数i(s)为零当
$ \begin{equation} s = e^{-(k+1)(1-s)} \end{equation} $
这是s的间接等式,但支配项显示s以指数为k的方式递减。这样递增的k是一个有效的方法确保大多数人听到了流言。例如,当k = 1该公式建议20%将错过该流言,当k = 2只有6%会错过
-
变化
目前我们只看到一个复杂的传染病,基于流言扩散技术。一般我们想要理解如何设计一个好的流行病,这样它值得现在暂停下来审查判断传染病的标准。我们考虑:
- 留数 当i为0时s的值,当传染病完成时仍然可怀疑的数量。我们想要留数尽可能小,且如上所分析的,它可很灵活的使留数任意小
-
流量 目前我们以站点间数据库更新的方式度量流量,不考虑网络拓扑。这方便使用一个平均值m,一个典型站点发送消息的数量:
$ \begin{equation} m = \frac{ \text{总更新流量} }{ 站点数 } \end{equation} $
在第3节我们将提炼该度量来兼容个人连接的流量
- 延迟 有两个有趣的时间。平均延迟是在一个给定站点更新初始注入和更新达到时间之间的不同,在所有站点的评价。我们引用它为 $ t_ {ave} $。一个相似的数量,$ t_ {last} $为传染病期间接受到更新的最后一个站点的延迟。在$ t_ {last} $之后更新消息将持续出现在网络,但它们将不会到达一个怀疑站点。我们发现它需要引入两个时间因为它们常常行为不同,且设计者逻辑上会担忧这两个时间
接下来,让我们考虑一些流言扩散的变动。首先我们将描述修改的实际方面,且之后我们将讨论留数、流量和延迟
Blind vs Feedback 流言例子使用接收者的反馈;一个发送者丢失兴趣仅在接收者已知该流言。一个盲变化以1/k的概率丢失兴趣而不考虑接收者。这移除了对接收者向量响应的需要。
Counter vs Coin 我们使用一个计数来替代已概率1/k丢失兴趣,这样我们丢失兴趣仅在k个不必要的联系之后。计数需要保持感染列表元素的额外状态。注意我们可组合计数和盲技术,独立于任何反馈仍然感染k个循环
以上变化的一个奇怪的方面是它们共享相同的流量和留数之间的基本关系:
$ \begin{equation} s = e^{-m} \end{equation} $
通过观察nm个更新发送和单个站点遗失所有这些更新的机会是 $ (1 - \frac{1}{n})^{nm} $我们可以得出该公式。(因为m不是个常量该关系依赖m的分布走到0当 $ n \to \infty $,这个事实是我们已观察到但没有证明)延迟是区分以上可能性的唯一考量:模拟显示计数和反馈改善延迟,计数扮演了一个比反馈更重要的角色
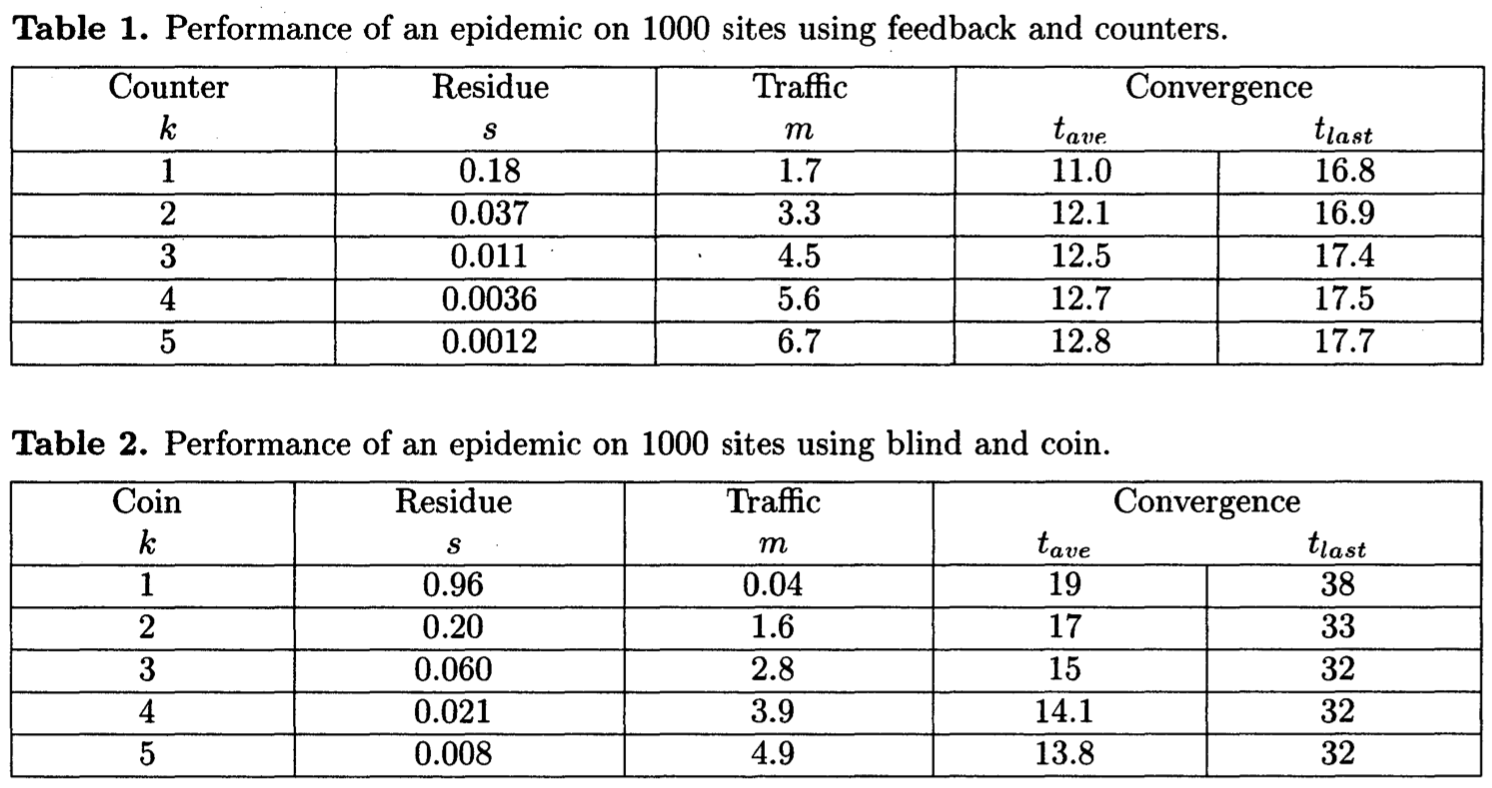
推 vs 拉, 我们假设所有的站点随机选择目标站点并推感染更新给目标。反熵推 vs 拉的不同可被应用到流言。拉有一些优点,但主要实际考虑是更新注入到分布式数据库的速度。如果有大量独立的更新一个拉请求很可能找到一个非空流言列表的源,触发有用的信息流。相反,如果数据库不活跃,推算法停止引入过量流量,当拉继续注入更新请求时。我们自己的CIN应用程序有一个足够高的更新速度来警告拉的使用
拉的主要优势是它比推关系的 $ s = e^{-m} $更好。这里blind vs feedback和counter vs coin变种很重要。模拟显示counter和feedback变种改进留数,counter比feedback更重要些。我们有复现关系建模counter和feedback例子显示 $ s = e^{- \Theta(m^{3})} $的行为

最小化 它也可能使用计数器的两个参与者做一个交换来做出一个删除决定。该想法使用一个推和拉,且如果两个站点知道了该更新,则有更小计数的站点将增长(如果相等则都会增长)。这需要通过网络发送一个计数器
连接限制 是否连接限制应视为一个难点或一个优点不是很清楚。这样我们忽略连接限制。在推模型下,例如,我们已假设在单个循环中一个站点更可能变为一个接收者而不是一个推送者,且在推的例子中我们假设一个站点可服务无限制数量的请求。因为我们计划频繁运行流言扩散算法,现实中我们使用一个连接限制。连接限制影响推和拉机制有些不同:拉会更差,推更好些
为了解为什么推更好,假设数据库比较安静,只有一个更新在扩散,且连接限制为1。如果两个站点联系相同的接收者则一个联系被拒绝。接收者仍然获得更新,但少一个单位流量。(我们已选择用更新发送来度量流量。一些网络活动引起拒绝连接,但这传输的更新要少。我们有,缺失连接否则无用)。多少连接被拒绝?因为一个流行病指数增长,我们假设多少流量发生在最后当几乎每个人被感染且拒绝的概率接近 $ e^{-1} $。所以我们期望推及连接限制1行为如下:
$ \begin{equation} s = e^{- \lambda m } \qquad \qquad \lambda = \frac{1}{1 - e^{-1}} \end{equation} $
模拟显示计数变化接近这个行为(计数及反馈有效)。coin变种不符合以上假设,因为当所有站点感染时它们没有最多的流量发生。虽然它们仍然比 $ s = e^{-m} $好。所有的变种,因为推在安静的网络中以连接限制1最好它似乎值得强制该限制即使更多的连接是可能的
有连接限制的拉会差些,因为好的性能依赖每个循环在每个站点为一个接收者。虽然有一个有限的连接失败概率 $ \delta $,拉变动的渐近线。假设,最多的流量发生在所哟站点被感染时,则在该期间一个站点丢失一个更新的机会大约为:
$ \begin{equation} s = \delta^{m} = e^{- \lambda m } \qquad \qquad \lambda = - \ln \delta \end{equation} $
幸运地是,对适度大小的连接限制,失败概率变得非常小,因为在一个循环中一个站点有j个连接的机会为 $ \frac{e^{-1}}{j !} $
搜寻 如果一个连接被拒绝则选择站点可搜寻替代站点。搜寻是相对便宜的且似乎能改善所有连接限制的情况。在极端情况下,一个连接限制为1及无限搜寻限制导致一个完全的排列。推和拉变得相同,且余留非常小
提供一个反熵的复制流行病
我们看到一个复杂的流行病算法可以非常小的流量快速扩散更新。不幸地是,一个复杂的流行可能失败;有一个非零的概率感染站点数量将为零当某些站点依然是怀疑状态时。这种事件很少出现;虽然,如果它发生,系统将在一个稳定状态一个更新被某些站点所知,但不是所有站点。为消除这种可能性,反熵可间断运行来支持一个复杂流行,如同在Clearinghouse中支持直接邮件一样。这确保概率为1的使每个更新最终到达(或被替换)每个站点
但反熵作为一个支持机制,对初始化更新来说流言传播比直接邮件有显著的优势。考虑当一个丢失更新被发现当两个站点执行反熵时做了什么。一个传统的响应不会做任何事(除了使数据库两个站点一致),依赖反熵最终转发更新到所有站点。一个更积极的响应会重分布更新,使用机制初始化分布,例如,邮件它到所有其他站点或使它再成为一个热流言。保守的处理是少数站点不知道更新。然而,处理偶尔完全的初始化失败,需要一个重分布步骤
不幸地是,直接邮件重分布的开销很高。最坏的情况发生在当初始化分布管理转发一个更新到大约一半的站点,这样下一个反熵循环每个O(n)站点尝试重分布更新通过邮件它到所有n个站点,产生 $ O(n^{2}) $个邮件消息。Clearinghouse首次实现重分布,但我们强制消除它因为它开销太高
使用流言传播而不是直接邮件会极大缩减重分布的期望开销。流言传播在简单情况下是理想的,只有几个站点接收更新失败,因为一个热流言已经被几乎所有站点知道这样它会快速消失不会产生很多流量。它在最坏的情况下表现也不错:如果一个更新分布到大约一半的站点,则O(n)个更新拷贝将作为热流言引入下一个反熵轮次。这实际上比在单个站点引入流言产生更少的网络流量
这使我们产生一个组合流言传播和反熵的方式。回忆我们之前描述一个反熵的变种成为peel back需要一个额外的以时间戳为序的数据库索引。该想法使站点已反时间戳序交换更新直到它们在整个数据库上达成checksum一致。peel back和流言传播可组合通过保持一个双向列表的更新而不是一个搜索树。在我们需要一个搜索树来维持反向时间戳顺序之前,我们现在使用一个双向链表维持一个本地活动顺序:站点发送更新根据他们的本地链表序,且它们接收通常的流言反馈告诉它们什么时候一个更新有用。有用的更新移动到它们对应列表的前面,而无用的更新变得在列表深处。这种组合变种比只用peel back更好因为:1)它避免了额外的索引,2)它在网络分区和重加入时表现很好。它比只使用流言传播要好因为它没有失败可能性。在实际中,我们可能在某时间不发送更新,但从列表头批量一系列更新。这个集合模拟流言传播的热流言列表,但成员关系不再是二进制方式因为如果第一个批量达成checksum一致失败的话,则更多的批量会发送。如果必要,数据库的任意更新可再变为热流言
删除和死亡证书
使用反熵或留言传播,我们不能简单通过删除本地拷贝的项目来删除数据库中项目,期望项目的缺失扩散到其他站点。相反会发生:广播机制将扩散项目的旧拷贝在我们删除数据库项目之前。除非我们同时删除数据库所有拷贝中的过期项目,它会最终恢复
为弥补这个问题我们用死亡证书替代项目的删除,其也携带时间戳且如同普通数据一样扩散。在广播期间,当老的拷贝的删除项目遇到死亡证书,老的项目被删除。如果我们保持一个死亡证书足够长时间它最终取消所有老的拷贝的相关项目。不幸地是,死亡证书本身或它们将最终在所有站点耗费所有存储
我们的策略是持有每个死亡证书直到它确定每个站点已接收。Sarin和Lynch描述了一个协议来做这个确定,基于Chandy和Lamport的分布式快照算法。独立的协议需要添加和删除站点(Sarin和Lynch不描述站点添加协议的任何细节)。如果在死亡证书的创建和分布式快照完成期间任意站点永久故障,死亡证书不能删除直到站点移除协议已被运行。对数百个站点的网络该事实是非常重要的。在我们的经验中,有一个非常高的概率在任意时刻某些站点将出问题或不可达数小时或几天,阻止分布快照或站点删除算法完成
一个更简单的策略是持有死亡证书某个固定时间,比如30天,然后丢弃它们。这种方案,我们有遗弃项目存在超过恢复期的风险。有一个清晰的妥协在死亡证书空间和遗弃项目恢复风险之间:增加时间阙值减少风险但增加死亡证书的空间消耗
搁浅死亡证书
有一个分布式方法扩展时间阙值减少在任意服务器空间上的持有。该方案,我们称为搁浅死亡证书,基于如下观察。如果死亡证书比期望广播到所有站点的时间更老,则不太可能存在对应数据项目的遗弃拷贝在网络上。我们可在大多数站点上删除非常老的死亡证书,只在几个站点上保持搁浅拷贝。当一个遗弃更新计数一个搁浅死亡证书,该死亡证书会被唤醒且重现广播到所有站点。该操作是昂贵的,但它不频繁发生。这种方式我们可确保如果一个死亡证书在网络任意站点,恢复相关数据项目将不会持有任意明显的时间。注意一个免疫行为的模拟,唤醒死亡证书行为像抗体
实现使用两个阙值,$ \tau_ {1}和\tau_ {2} $,且附带一个对每个死亡证书的一个持有站点名列表。当一个死亡证书被创建,它的持有站点被随机选择。死亡证书被使用相同机制的普通更新广播。每个服务器保存所有时间戳为当前时间 $ \tau_ {1} $ 的死亡证书。一旦 $ \tau_ {1} $达到,大多数站点删除死亡证书,但死亡证书持有站点列表的每个服务器保存可激活的拷贝,它们在 $ \tau_ {1} + \tau_ {2} $时间后被抛弃
(为简化我们忽略站点本地时钟的不同。它是真实的假设时钟同步错误最多 $ \epsilon « \tau_ {1} $。这在讨论中没有影响)
待激活死亡证书偶尔会由于服务器的持久故障而丢失。例如,在一个服务器半生命概率下所有服务器持有给定死亡证书的待激活拷贝故障为 $ 2^{-r} $,r值可被选择使得概率为可接受的小数
比较这个方案和使用单个固定阙值 $ \tau $的方案,假设删除速度在时间上稳定,对相等的空间使用,假设 $ \tau > \tau_ {1} $,我们获得
$ \begin{equation} \tau_ {2} = (\tau - \tau_ {1})n / r \end{equation} $
即,我们可维护在总的历史统计上有O(n)的改进。在我们现存的系统中,这使得我们增加有效历史从30天到数年
待激活死亡证书算法似乎可被无限扩展,但不幸地是,这是不行的。问题是广播一个新的死亡证书到所有站点的期望时间,当增长n,将最终超过阙值 $ \tau_ {1} $,其不随着n增长。当广播时间小于 $ \tau_ {1} $,它很少需要重激活老的死亡证书;在广播时间增长超过 $ \tau_ {1} $之后,重激活老的死亡证书变得越来越频繁。这引入额外的网络负载来广播老的死亡证书,因此进一步增加广播时间。最终的结果是严重的故障。为避免这种故障,系统参数必须选择为保持期望广播时间在$ \tau_ {1} $之下。如上描述,一个新的更新使用反熵通过网络需要的时间期望为O(logn)。这意味着对有效大型网络 $ \tau_ {1} $,每个服务器需要的空间,最终必须增长O(logn)
待激活死亡证书反熵
如果反熵用来做分布式更新,待激活死亡证书应该在反熵交换期间不能正常广播。当一个待激活死亡证书记为一个遗弃数据项,然而,死亡证书必须以某种形式激活,所以它将广播到所有站点且取消遗弃数据项
激活一个死亡证书一个明显的方式是设置它的时间戳为当前时钟值之前,这种处理会被系统接受不允许删除数据项为复原的。一般情况下这是不对的,因为在网络中可能有一个非法的更新带一个时间戳为原始和死亡证书恢复时间戳(例如,一个更新恢复一个删除项)之间。这样一个更新将错误的被激活死亡证书取消
为避免这个问题,对每个死亡证书,我们存储第二个时间戳,称为激活时间戳。初始化普通和激活时间戳是一样的。一个死亡证书仍然取消一个对应的数据项如果它的普通时间戳大于该项目的时间戳。然而,激活时间戳控制是否一个死亡证书是暂停的且它如何广播。特别地,一个死亡证书被删除(或被一个在它的站点列表中的站点认为是暂停的)当它的激活时间戳超过 $ \tau_ {1} + \tau_ {2} $;且一个死亡证书被反熵广播只在它不是暂停的。为重激活一个死亡证书,我们设置它的激活时间戳为当前时间,使它的普通时间戳不变。这使得广播重激活死亡证书的影响不取消更多的现在的更新
暂停的死亡证书的流言广播
激活时间戳机制描述对反熵起作用同样对分布式更新中使用的流言广播也起作用。每个死亡证书被创建作为一个激活的流言。最终它通过网络广播且变得在所有站点不激活。无论何时一个暂停的死亡证书在某些站点记录一个遗弃数据项,死亡证书通过设置它的激活时间戳为当前时间来激活。另外,它制作又一个流言。正常的流言广播机制然后通过网络分布重激活死亡证书
空间分布
到目前为止我们认为网络是统一的,但实际上发送一个更新到附近站点的开销远小于发送到远端的站点。为减少通讯开销,我们想我们的协议更愿意使用附近的邻居,但这导致过于本区域,最简单的办法是用一条线扩展这个折中
假设,某时刻,数据库站点排列在线性网络上,且每个站点有一个从最近邻居的连接。如果我们仅使用最近的邻居来交换反熵,则每个连接上的流量为O(1),但它将花费O(n)循环来扩散一个更新。另一个极端,如果我们使用统一的随机连接,则连接的平均距离为O(n),这样即使收敛为O(logn),每个连接的流量每次循环为O(n)。一般地,设连接一个距离为d的站点的概率为 $ d^{-a} $,a是一个被确定的参数。分析显示每个连接期望的流量为
$ \begin{equation} T(n) = \left\{ \begin{array}{ll} O(n), & a < 1; \\ O(\frac{n}{\log n}), & a = 1; \\ O(n^{2 - a}), & 1 < a < 2; \\ O(\log n), & a = 2; \\ O(1), & a > 2. \end{array} \right. \end{equation} $
$ d^{-a} $分布的收敛时间很难计算精准。非形式化等式和模拟建议它们符合反面范型:对a > 2收敛是n的多项式,且对a < 2收敛是多项式logn。这个强烈建议使用 $ d^{-2} $分布在一条线上扩散更新,因为流量和收敛当n趋于无穷时扩展性很好
现实的网络与上面的线性例子几乎没有相似之处(奇怪地是,CIN的小部分事实上是线性的,但大部分网络是高度连接的),所以它不能立即明显的如何产生 $ d^{-2} $分布。以上推理可被一般化到高维直线网站网格,建议好的收敛(多项式为logn)的分布接近 $ d^{-2D} $,D是网格维度。更进一步,当分布为 $ d^{-(D+1)} $时流量掉到 $ O(\log{n}) $,这样我们有一个更广领域的行为,但它依赖网格维度D。这个观察让我们考虑使每个网站根据分布函数 $ \mathcal{Q}_ {s}(d) $独立选择连接,$ \mathcal{Q}_ {s}(d) $是从s距离小于等于d的网站数量。在一个D维网格,$ \mathcal{Q}_ {s}(d) $是 $ \Theta(d^{D}) $,这样一个分布如 $ \frac{1}{\mathcal{Q}_ {s}(d)^{2}} $是 $ \Theta(d^{-2D}) $,不管网格维度是多少。我们推测 $ \mathcal{Q}_ {s}(d) $函数适配网格维度的能力使它在任意网络中都工作得很好,且渐进属性使分布在 $ \frac{1}{d\mathcal{Q}_ {s}(d)} $和 $ \frac{1}{\mathcal{Q}_ {s}(d)^{2}} $之间有很好的扩展属性。下一节描述更近一步的对分布选择实践考虑和 $ \frac{1}{\mathcal{Q}_ {s} (d)^{2}} $的我们的经验
空间分布和反熵
以上我们讨论一个非统一空间分布可显著地减少反熵产生的流量,且不会在它的收敛时间内不可接受地增长。网络拓扑考虑为规则的:D维直线网格
使用一个非统一分布变得更有吸引力当我们考虑事实上的CIN拓扑。特别地,CIN包括关键连接的小集合,比如一对跨大西洋连接唯一路由连接欧洲 $ n_ {1} $站点到北美的 $ n_ {2} $站点。当前 $ n_ {1} $是几十个,且 $ n_ {2} $为数百个。使用一个统一的分布,在这些跨大西洋连接每轮反熵会话的期望数为 $ \frac{2n_ {1}n_ {2}}{(n_ {1} + n_ {2})} $。在两个连接间共享大约80个会话。通过比较,当在所有连接上平均,每个循环每次连接期望的流量少于6个会话。这在关键连接上是不可接受的高流量,而不是每连接平均流量,使我们的系统中使用统一反熵太昂贵。这个观察激发我们对非统一空间分布的学习
为学习网络流量如何缩减,我们使用实际的CIN拓扑和一些不同的空间分布执行反熵行为的扩展模拟
初步的结果显示 $ \mathcal{Q}_ {s}(d) $的分布参数很好地适配本地维度的网络,且执行明显好过任意直接依赖d的分布。特别地,$ \frac{1}{\mathcal{Q}_ {s}(d)^{2}} $比 $ \frac{1}{d \mathcal{Q}_ {s}(d)} $更好。使用形如 $ \mathcal{Q}_ {s}(d)^{-a} $空间分布反熵的结果非常令人鼓舞。然而,早期的流言传播模拟未覆盖当空间分布使用时CIN拓扑的一些问题
在检查这些结果后,我们发展了一个不同的分布类型,其对突然增加的 $ \mathcal{Q}_ {s}(d) $更不敏感。这些分布证明对CIN拓扑中的反熵和流言传播更有效。非形式化的,让每个站点s根据从s的距离排序构建一个其他站点的列表,且然后从列表中根据函数f(i)选择反熵交换合作者。该函数给定选择一个站点的概率如同在列表中它的位置i的函数。对f我们可使用在统一线性网络中使用的空间分布函数。当然,在实践网络中从s有相同距离的两个站点(但在列表中不同的位置)不应该为不同的概率被选择。我们可通过选择相同距离站点的平均概率排列,例如,通过选择在距离d以概率比例的每个站点为
$ p(d) = \frac{\sum^{\mathcal{Q}(d)}_ {i=\mathcal{Q}(d-1)+1} f(i)}{\mathcal{Q}(d) - \mathcal{Q}(d - 1)} $
设 $ f = i^{-a} $,a是一个确定的参数,且通过积分估计和,我们获得
$ p(d) \approx \frac{\mathcal{Q}(d - 1)^{-a+1} - \mathcal{Q}(d)^{-a+1}}{\mathcal{Q}(d) - \mathcal{Q}(d - 1)} $
对a = 2右边缩减为
$ 1 / (Q_ {s}(d - 1) Q_ {s}(d)) $
在D维mash上是 $ O(d^{-2D}) $
模拟结果报告使用要么统一分布要么上述选择a值的分布(为避免 $ \mathcal{Q}(d) = 0 $的单点我们通过上述等式增加1到 $ \mathcal{Q}(d) $
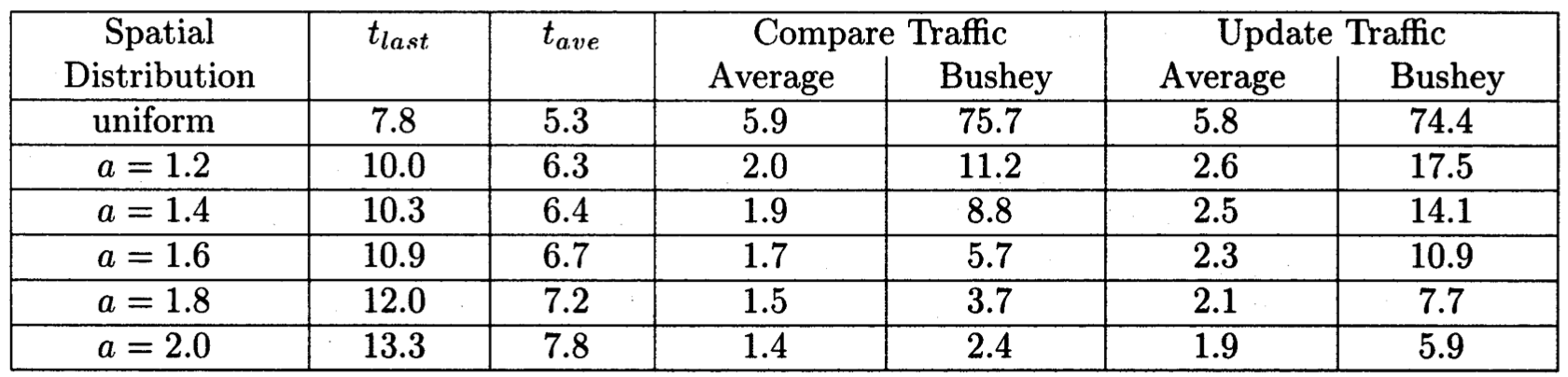
上图总结CIN拓扑使用推拉反熵及无连接限制的结果。该表呈现250个运行,每个广播单个更新在随机选择站点引入。比较流量部分代表每周期反熵比较数量,所有网络连接平均和单独跨太平洋连接到英格兰Bushey的平均。更新流量代表反熵交换的总数量,该更新从一个站点发送到另一个站点(比较和更新流量的不同是明显的如果checksum用于数据库比较)
有亮点值得提及;
- 比较a = 2的结果和统一的情况,收敛时间 $ t_ {last} $降级小于2,然而每轮平均流量改进超过4。有争论地是,我们可以负担执行反熵为非统一分布的2倍,因此获得一个相对收敛速度在平均流量下为2
- 比较a = 2的结果和统一的情况,跨太平洋连接失败的比较流量从75.7变为2.4,超过30倍。该连接流量现在小了两倍。我们视它为CIN拓扑下非统一分布最重要的好处。使用这个分布,反熵交换不会过载关键的网络连接
上图的结果假设无连接限制。该假设是非常不现实的 - 实际的ClearingHouse服务器可支持一次少数的反熵连接。下图给出在最悲观假设下模拟结果:1个连接限制和hunt连接为0。该图呈现250个运行,每个广播单个更新引入在一个随机选择站点
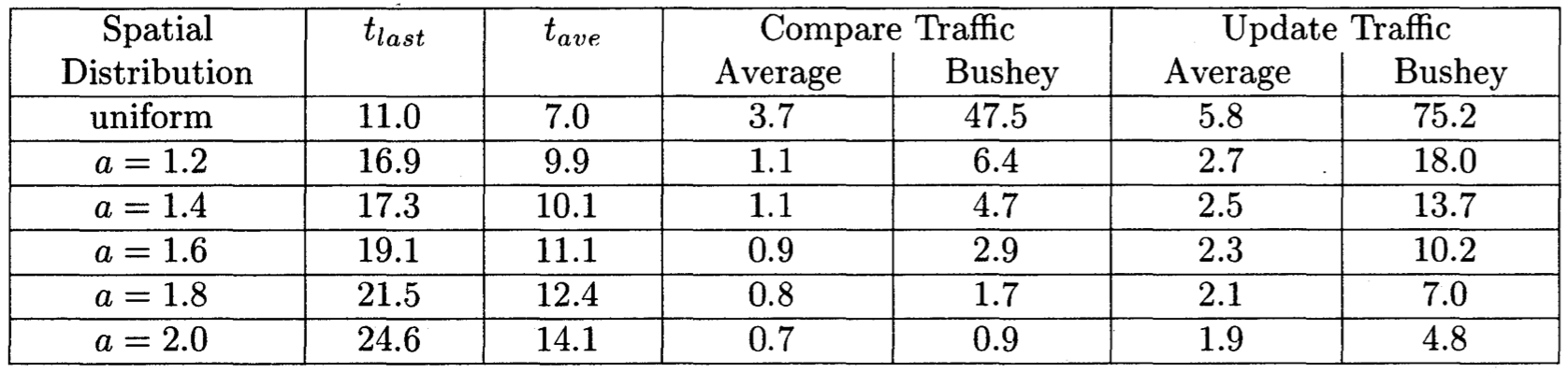
注意:
- 上图中比较流量比前面的图要低,对应事实是每周期成功建立的连接数要少。上图收敛时间相对之前的图要高。这些影响表现为更少的统一分布
- 总比较时间(收敛时间和比较流量的乘积)当连接限制被强制时没有显著变化;每循环比较流量减少,循环数增加
总结:使用反熵的空间分布在统一分布情况下在关键连接为蜜罐时可显著减少流量。最悲观的连接限制减慢收敛但没有明显改变分布更新时产生的总流量数;它只是减缓更新分布
基于我们之前模拟结果,一个非统一反熵算法使用 $ 1 / Q(d)^{2} $分布被实现作为Clearinghouse服务的内部版本的一部分。新版本已安装在整个CIN且在Clearinghouse服务器和它们数据库一致性产生的网络负载上有明显改进
空间分布和流言
因为反熵在每次交换有效地检查整个数据库,因此它非常健壮。例如,考虑一个空间分布使得对站点的每对 $ (s, s^{\prime}) $有一个非空的概率s会选择与 $ s^{\prime} $进行数据交换。容易显示用这样的分布反熵会以概率1收敛,因为在这些条件下每个站点最终和其他站点直接交换数据
散布流言在另一方面,运行比较安静 - 每个流言最终变得不活跃,且如果它在一定时间内没有扩散到所有站点它将不会扩散。这样它是不充分的使站点持有一个新的更新最终联系到其他站点;该联系必须发生得足够快否则更新不能扩散到所有站点。这使得流言散布稳健性不如反熵
流言散布有一个参数可以进行调整:作为空间分布缺少统一,我们可增加流言散布算法中的k值来补偿。对在CIN拓扑中的推拉流言散布,该技术非常有效。我们在之前的章节中模拟了流言散布的变种,使用增加非统一空间分布。我们发现一旦k值调整到在每200个尝试中给定100%的分布,流量和收敛时间值结果在上表4中。一个有限小数k取得和 $ k = \infty $一样的结果
上表4中收敛时间给定为周期内。然而,一个反熵周期的开销是数据库大小的函数,而流言散布周期的开销是系统中活动流言数量的函数。相似地,表4中流量比较当解释为从属于反熵或流言散布时有不同的含义。在一般流言散布比较会比反熵比较更廉价,因为它们只需要检查热流言列表
我们得出一个非统一空间分布可产生一个有价值的改进在推拉流言散布的性能上,特别在关键网络连接流量上
在非统一空间分布和任意网络拓扑中流言散布的推和拉变种出现比推拉更敏感。使用(反馈、统计、推、无连接限制)流言散布和a = 1.2的空间分布,k值需要达到在每200个模拟尝试中100%空间则需要为36;收敛时间相应高。更大的a值模拟不能完全在一晚上做完,所以这样的尝试被放弃
我们还没有完全理解该行为,但两个简单的例子显示问题的种类会提升。两个例子都依赖隔离站点,相对其他网络比较远
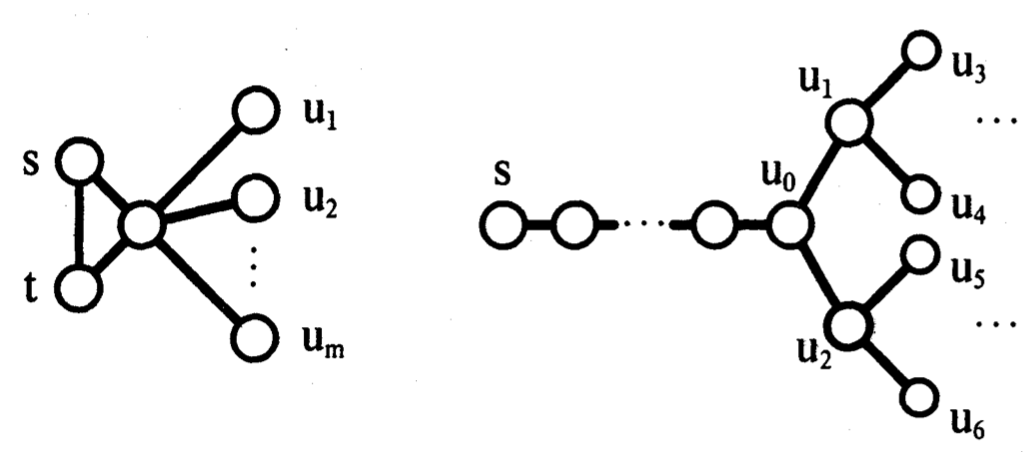
首先,考虑上图左图中的网络,两个站点s和t互相很近且跟其他站点 $ u_ {1}, \ldots, u_ {m} $远,但它们到s和t的距离相等(容易构建这样的网络,因为我们不需要有一个数据库站点在每个网络节点)。假设s和t使用 $ Q_ {s}(d)^{-2} $分布来选择合作者。如果m比k大有一个重要的概率s和t会互相选择对方作为合作者在k个连续循环中。如果推流言传播被使用且一个更新被s或t引入,该结果在一个灾难性故障中 - 更新被转发到s和t;在k次循环后它没有转发到任何站点则停止作为一个热流言。如果拉模式被使用,更新在网络主要部分被引入,有一个关键的机会每次s或t联系一个站点 $ u_ {i} $,站点不知道该更新或知道很久了它不再是一个热流言;结果是s和t都没有学习到更新
作为第二个例子,考虑一个网络如上图右图。站点s连接一个完全二叉树的n - 1个站点的根 $ u_ {0} $,从s到 $ u_ {0} $的距离大于树的高度。假设所有站点使用 $ Q_ {s}(d)^{-2} $分布来选择流言广播合作者。如果n相对k很大,有一个重要的概率在k次连续循环中没有树中的站点尝试联系s。使用推流言广播模型,如果一个更新在树的某些节点被引入,更新可能不能转发到s直到它停止作为一个热流言
在空间分布和非规则网络拓扑间完全理解需要更多地学习。上述的例子和模拟结果强调了用反熵备份流言广播的需要来保障完全覆盖。给定这样的一个保障,然而,空间分布的推拉流言广播在CIN中出现非常有吸引力
结论
对有简单随机算法的复制数据库一致性替代复杂确定性算法是可能的,需要一些底层通讯系统的保障。在施乐公司网络实现的随机反熵算法在达到一致性和减少网络过度流量这两方面都提供了令人印象深刻的性能。通过使用一个选择好的空间分布来选择反熵合作者,实现算法减少了平均连接流量超过因子4及某些关键连接流量减少了30,相比较使用统一合作者选择的算法
通过观察反熵行为像一个简单的流行病让我们考虑其他流行病相似算法比如流言传播,其显示承诺作为分布式更新的初始化邮递步骤的一个有效的替代。一个备份反熵方案容易扩散更新到不接受流言的站点。事实上,比较一个流言广播的反熵去皮版本,流言广播在完全扩散一个更新时绝不会失败
流行病算法和直接邮递算法在没有死亡证书辅助的情况下都不能正确地扩散一个项目的缺失。这是死亡证书保留时间、存储空间消费和不想要出现在数据库里的旧数据之间的妥协。通过重新获得一些站点的搁置死亡证书我们可显著改善网络对废弃数据在合理存储消费上的免疫力
有更多的问题需要探索。网络路径拓扑代表性能问题。一个解决方案需要找到算法使得所有拓扑都能很好工作;否则,这会变成路径拓扑的特征。在分析和设计流行病上仍然有许多工作。我们已避免服务器上的不同,构建一个动态分层可能获得更好地性能,高层站点在长距离上联系其他高层服务器,底层服务器有短的距离(这样的机制的关键问题是维护一个分层结构)
Tips
- 知识分类型,一些大量消耗脑细胞的需要放慢速度有效吸收,而一些更偏知识型的,可以提速以了解阅读为主
- 注意前提知识,在学习新的知识前先把其需要的前提知识先学好,有层次的推进,否则容易卡壳
- 或许每个阶段有每个阶段适合自己的学习方法,在未找到更好的方法之前先要坚持使用目前认为最适合的方法,并清楚当前所用方法的缺陷及可能改进方向,每过一段时间或觉得当前方法不再适应时,要尝试一些新的方法
Share
Scalability for Dummies - Part 2: Database
https://www.lecloud.net/post/7994751381/scalability-for-dummies-part-2-database
在第一部分之后,你的服务器现在可水平扩展且你可服务数千个并行请求。但你的应用程序变得越来越慢且最终无法工作。原因:你的数据库。是MySQL?
现在需要的改变比添加更多的复制节点更加激进且需要一些勇气。最后,你可选择2条路:
路径1是继续使用MySQL并使他运行。租用一个数据库管理员(DBA)告诉他做主从复制(从节点读,主节点写)且添加内存来升级你的主服务器。在数月时间,你的DBA将提及“分片”,“denormalization”, “SQL tunning”且担心下周过多需求。这时每个保持数据库运行的新的行为 将更昂贵且耗时。如果你的数据集较小且容易迁移你可能选择路径2更好
路径2意味着从开始阶段就denormalize right且在任意数据库查询中不包含Join。你可停留于使用MySQL,且像NoSQL数据库一样使用它,否则你可以切换到一个更好更易扩展的NoSQL数据库如MongoDB或CouchDB。Join现在需要在你的应用程序代码中做。这个步骤你做的越快将来需要修改的代码越少。但即使你成功切换到最新最好的NoSQL数据库且让你的应用程序做数据集join,不久你的数据库请求将变得越来越慢,你需要引入缓存